贝叶斯分类算法

贝叶斯分类算法

贝叶斯分类算法是统计学的一种分类方法，它是一类利用概率统计知识进行分类的算法。在许多场合，朴素贝叶斯(Naïve Bayes，NB)分类算法可以与决策树和神经网络分类算法相媲美，该算法能运用到大型数据库中，而且方法简单、分类准确率高、速度快。

朴素贝叶斯算法

设每个数据样本用一个n维特征向量来描述n个属性的值，即：X={x1，x2，…，xn}，假定有m个类，分别用C1, C2,…，Cm表示。给定一个未知的数据样本X（即没有类标号），若朴素贝叶斯分类法将未知的样本X分配给类Ci，则一定是

$P(Ci|X)>P(Cj|X)1\le j\le m，j\ne i$

根据贝叶斯定理
由于P(X)对于所有类为常数，最大化后验概率P(Ci|X)可转化为最大化先验概率P(X|Ci)P(Ci)。

如果训练数据集有许多属性和元组，计算P(X|Ci)的开销可能非常大，为此，通常假设各属性的取值互相独立，这样
先验概率P(x1|Ci)，P(x2|Ci)，…，P(xn|Ci)可以从训练数据集求得。

根据此方法，对一个未知类别的样本X，可以先分别计算出X属于每一个类别Ci的概率P(X|Ci)P(Ci)，然后选择其中概率最大的类别作为其类别。

朴素贝叶斯算法成立的前提是各属性之间互相独立。当数据集满足这种独立性假设时,分类的准确度较高，否则可能较低。另外，该算法没有分类规则输出。

在贝叶斯分类中，我们感兴趣的是在给定一些观察到的特征的情况下找到标签的概率，我们可以将这些特征写成P(L | features)P(L | features) 。贝叶斯定理告诉我们如

P(L | features)=P(features | L)P(L)P(features)
P(L | features)=P(features | L)P(L)P(features)

在两个标签之间做出决定，我们称它们为L1L1 和L2L2，那么做出这个决定的一种方法是计算每个标签的后验概率之比

P(L1 | features)P(L2 | features)=P(features | L1)P(features | L2)P(L1)P(L2)
P(L1 | features)P(L2 | features)=P(features | L1)P(features | L2)P(L1)P(L2)

代码开干

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

先搞定数据

from sklearn.datasets import make_blobs
X, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu');

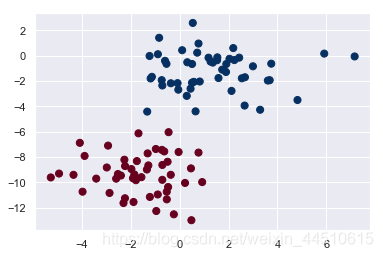
在使用MultinomialNB分类器训练时，如果输入数据出现负值，会出现"ValueError: Input X must be non-negative"的错误。解决办法，将MultinomialNB换成 GaussianNB即可。

这种朴素高斯假设的结果如下图所示：

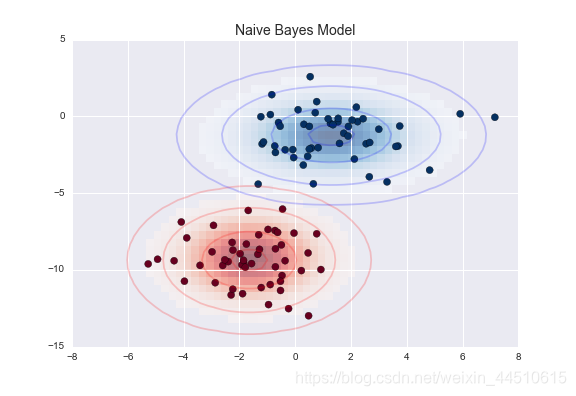
这里的椭圆代表每个标签的高斯生成模型，有更大的概率朝向椭圆的中心

高斯朴素贝叶斯 Gaussian Naive Bayes

from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X, y)

rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model.predict(Xnew)
ynew
# array([1, 1, 1, ..., 0, 1, 1])

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='RdBu', alpha=0.1)
plt.axis(lim)

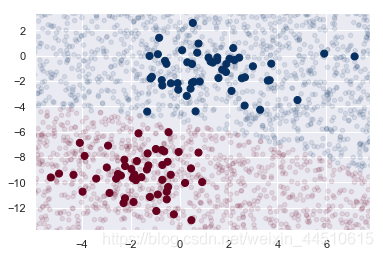
高斯朴素贝叶斯的边界是二次的

yprob = model.predict_proba(Xnew)
yprob[-8:].round(2)

array([[0.89, 0.11],
       [1.  , 0.  ],
       [1.  , 0.  ],
       [1.  , 0.  ],
       [1.  , 0.  ],
       [1.  , 0.  ],
       [0.  , 1.  ],
       [0.15, 0.85]])

除了高斯朴素贝叶斯，另一个有用的例子是多项式朴素贝叶斯（naive bayes），其中假定特征是由简单的多项式分布生成的。多项式分布描述了在许多类别中观察计数的概率，因此多项式朴素贝叶斯最适合表示计数或计数率的特征。

举例叙说贝叶斯分类算法

1. 收集大量的垃圾邮件和非垃圾邮件，建立垃圾邮件集和非垃圾邮件集。
2. 提取邮件主题和邮件体中的独立字符串，例如 ABC32，￥234等作为TOKEN串并统计提取出的TOKEN串出现的次数即字频。按照上述的方法分别处理垃圾邮件集和非垃圾邮件集中的所有邮件。
3. 每一个邮件集对应一个哈希表，hashtable_good对应非垃圾邮件集而hashtable_bad对应垃圾邮件集。表中存储TOKEN串到字频的映射关系。
4. 计算每个哈希表中TOKEN串出现的概率P=（某TOKEN串的字频）/（对应哈希表的长度）。
5. 综合考虑hashtable_good和hashtable_bad，推断出当新来的邮件中出现某个TOKEN串时，该新邮件为垃圾邮件的概率。数学表达式为：
   A 事件 ---- 邮件为垃圾邮件；
   t1,t2 …….tn 代表 TOKEN 串
   则 P （ A|ti ）表示在邮件中出现 TOKEN 串 ti 时，该邮件为垃圾邮件的概率。
   设
   P1 （ ti ） = （ ti 在 hashtable_good 中的值）
   P2 （ ti ） = （ ti 在 hashtable_ bad 中的值）
   则 P （ A|ti ） =P2 （ ti ） /[ （ P1 （ ti ） +P2 （ ti ） ] ；
6. 建立新的哈希表hashtable_probability存储TOKEN串ti到P（A|ti）的映射。
7. 至此，垃圾邮件集和非垃圾邮件集的学习过程结束。根据建立的哈希表 hashtable_probability可以估计一封新到的邮件为垃圾邮件的可能性。
   当新到一封邮件时，按照步骤2，生成TOKEN串。查询hashtable_probability得到该TOKEN 串的键值。
   假设由该邮件共得到N个TOKEN 串，t1,t2…….tn,hashtable_probability中对应的值为 P1 ， P2 ， ……PN， P(A|t1 ,t2, t3……tn) 表示在邮件中同时出现多个TOKEN串t1,t2……tn时，该邮件为垃圾邮件的概率。
   由复合概率公式可得P(A|t1 ,t2, t3……tn)=（P1P2……PN）/[P1P2……PN+（1-P1）（1-P2）……（1-PN）]，当 P(A|t1 ,t2, t3……tn) 超过预定阈值时，就可以判断邮件为垃圾邮件。

https://baike.baidu.com/item/%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%88%86%E7%B1%BB%E7%AE%97%E6%B3%95/7346561

好文
https://blog.youkuaiyun.com/guoyunfei20/article/details/78911721