压缩感知简单理解

压缩感知可以用来降维；同时也就可以用降维后的数据进行原始数据的还原。

1 一句话描述压缩感知

如果一个信号在变换域中是稀疏的，那么可以用一个和变换矩阵不相关的变换矩阵，再将稀疏信号变换到低维空间中。而基于该低维表示，可以用一个优化问题复原出高维信号。

2 流程

其流程↑简单如此，原始信号x可以通过线性变换${\psi }^{-1}$（傅立叶变换、小波变换）变成稀疏表示S，那么用观测矩阵$\varphi$对信号x进行随机亚采样，就可以得到低维表示。
$y=\varphi \psi S,即为y=AS$
若接收端得到了一个低维表式y，那么复原问题就变换为解上述等式。这里当满足RIP条件时（等价于$\varphi 与？$不相关），就可以用下述优化进行求解：

这个优化是NP-hard,所以又可以变换为下述优化：

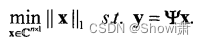
reference:

[1] 李豪, 形象易懂讲解算法II——压缩感知[D], https://zhuanlan.zhihu.com/p/22445302.