LeetCode最大正方形 动态规划

221. 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

示例 1：

 

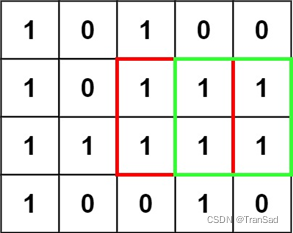
输入：matrix = [["1","0","1","0","0"],["1","0","1","1","1"],["1","1","1","1","1"],["1","0","0","1","0"]]

输出：4

示例 2：

 

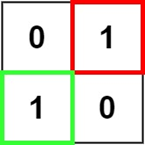
输入：matrix = [["0","1"],["1","0"]]

输出：1

示例 3：

输入：matrix = [["0"]]

输出：0

思路：

    这道题需要用到动态规划。

    直接说思路吧：我们定义二维数组dp[][],初始化就和原数组一模一样，dp[i][j]表示以这个位置为右下角所能组成的正方形的长度。

    举个例子，如下图所示：

 

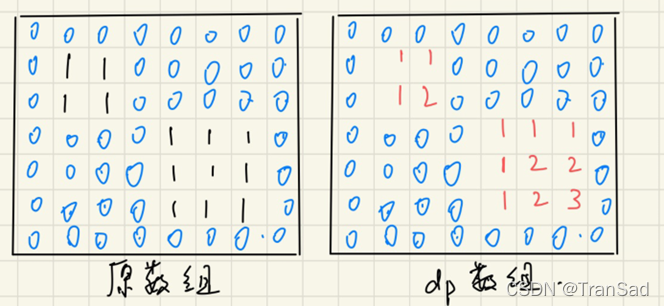
    原矩阵中有两个正方形，一个边长为2，一个边长为3，那么将它变成dp数组时，按照我们的定义：dp[i][j]表示以这个位置为右下角所能组成的正方形的长度，第一个正方形右下角的位置变成了2；第二个正方形中间位置变成了2，右下角变成了3……

进一步解释用图：

 

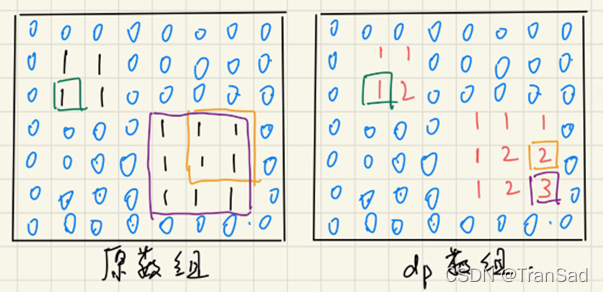
    再具体解释一下，比如dp数组中黄色框起来的，对应的就是原数组中黄色框起来边长为2的正方形，因为值为2；绿色框起来的1，对应的就是原数组边长为1的正方形；紫色框起来的3，则对应最大的边长为3的正方形。

    因此，只要我们得到了像右图这样的一个dp数组，我们就知道了最大正方形的边长，进而得到面积了。

    那怎么将原数组，转化成这样的dp数组呢？我们的状态转移方程该怎么写呢？我们从上到下，从左到右的遍历二维数组中的每一个格子，我们的每一个点都可以参照它的左上部分的三个位置。对于每个点，通过它左边、左上角、上边三个位置的“状态”，我们就可以“转移”出这个点的值。具体状态转移方程如下：

dp[i][j] = min(int(dp[i-1][j-1]),int(dp[i-1][j]),int(dp[i][j-1]))+1

    这里取min也很好理解，因为但凡左上三个位置中有一个不能组出够用的正方形，那么这个点肯定是没法变成大正方形的，类似木桶原理哈哈。

代码：

class Solution(object):
    def maximalSquare(self, matrix):
        #判断全篇是否有1
        flag=0
        for m in matrix:
            if '1' in m:
                flag=1
                break  
        if flag==0:#如果没有1 直接返回0
            return 0


		#正式开始，能到这里说明至少有一个1
        maxx = 1#最大正方形边长初始化为1
        dp = matrix[:][:]#dp可以初始化为matrix方便
        #dp[i][j]表示以（i，j）位置作为右下角组成的最大正方形的长度
        m = len(matrix)#拿到矩阵长度
        n = len(matrix[0])#宽度
        for i in range(1,m):#注意是从1开始，不是0开始
            for j in range(1,n):
                if matrix[i][j]=='1':#如果碰到了1，就使用状态转移方程
                    #相邻三块的长度取min再+1即可
                    dp[i][j] = min(int(dp[i-1][j-1]),int(dp[i-1][j]),int(dp[i][j-1]))+1
                    maxx = max(maxx,int(dp[i][j]))#尝试更新最大边长
        return maxx**2#返回的是面积，边长的平方

小结:

  关于代码中为什么要先处理那样的特殊情况，以及为什么两层循环是从1开始而不是0，其实如果不这么写，提交之后看到报错用例自然就明白了~  具体原因我写在下一段去吧。

  这是因为：为了让dp[i-1][j-1], dp[i-1][j]以及dp[i][j-1]有值，我们的两层循环是从(1,1)开始的，并不是（0，0）——这就导致对于只在最上面一行或者最左边一行有1的情况我们无法处理，所以要一开始全局判断一下。