golang 排序算法总结与实现

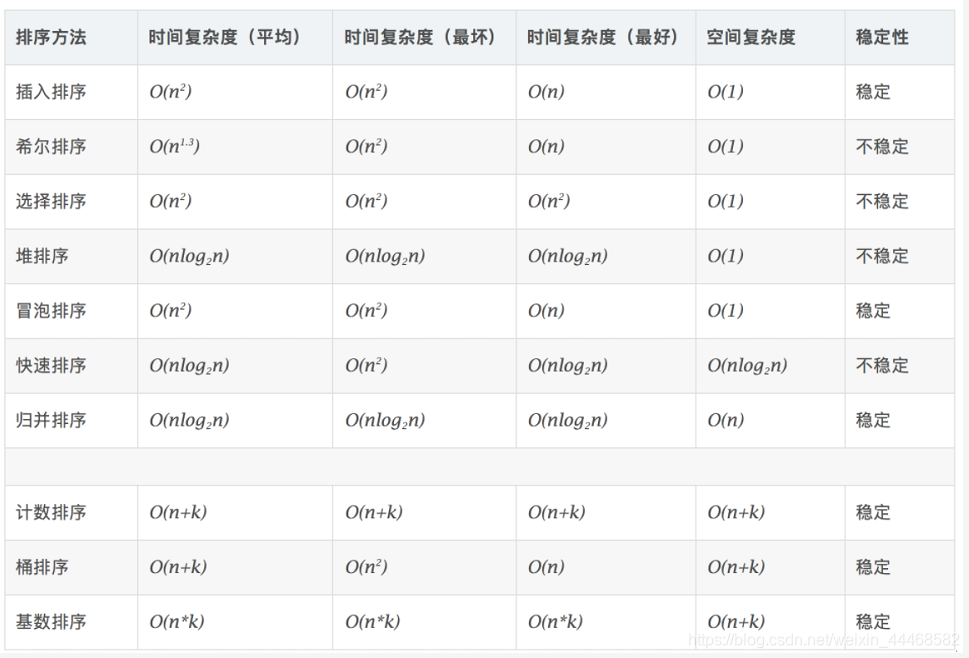
排序

插入排序

//InsertSort 插入排序 O(n2) (最好 O(n)) 稳定
func InsertSort(arr []int) {
	n:=len(arr)
	for i:=1;i<n;i++{
        v := arr[i]  //保存当前要比较插入的数
        for j:=i-1;j>=0;j--{ // 和之前所有数字比较
            if v <arr[j]{    // 小于的话 就交换   （所以稳定）
                arr[j+1]=arr[j]
            }else{
                arr[j+1]=v // 找到合适位置 插入
                break
            }
        }
	}
}

希尔排序（特殊的插入排序）将数组分组 （gap）表示同组元素索引差值

//HillSort O(n(1.3)) (时间复杂度与gap选取有关)不稳定
func HillSort(arr []int) {
	n := len(arr)
	for gap := n / 2; gap > 0; gap /= 2 {
		for i := gap; i < n; i++ {
			for j := i; j-gap >= 0; j -= gap { //插入排序
				if arr[j] < arr[j-gap] {
					arr[j], arr[j-gap] = arr[j-gap], arr[j]
				} else {
					break
				}
			}
		}
	}
}

选择排序 不稳定 （5 8 5 2 9） 第一遍交换了 5 2 两个5的相对顺序被破坏

//SelectSort 选择排序 O(n2) 不稳定
func SelectSort(arr []int) {
    n := len(arr)
    for i:=0;i<n-1;i++{
        min := i //存储索引 防止每次比较发生交换
        for j:= i+1;j<n;j--{
            if arr[j]<arr[min]{
                min = j
            }
        }
        if min!=i{ // 索引发生了变化 存在比当前小的 交换一次
            arr[i], arr[min]=arr[min],arr[i]
        }
    }
}

冒泡排序 数组有序下 优化 最优复杂度为On

//BubbleSort 冒泡排序 平均复杂度 O(n2) (最坏 O(n2) 最好(O(n)))稳定
func BubbleSort(arr []int) {
	n := len(arr)
	for i := 0; i < n-1; i++ {
		flag := true //flag为true 表示本次遍历未进行交换操作 最好情况有序 内层循环后没有发生交换 外层循环一次后break
		for j := 0; j < n-1-i; j++ {
			if arr[j] > arr[j+1] { //选择最大的  交换到最顶部 保证了稳定 相等不交换
				arr[j], arr[j+1] = arr[j+1], arr[j]
				flag = false
			}
		} 
		if flag {
			break
		}
	}
}

堆排序

//HeapSort O(nlogn) 不稳定  分为构建堆和调整堆两个步骤
func HeapSort(arr []int) {
	n := len(arr)
	if n == 0 {
		return
	}
	//自下而上构造大根堆  从最后一个非叶子节点开始调整
	for i := n/2 - 1; i >= 0; i-- {
		heapify(arr, i, n)
	}
	for j := n - 1; j >= 0; j-- {
		arr[0], arr[j] = arr[j], arr[0]
		heapify(arr, 0, j-1)
	}
}

//heapify 调整
func heapify(arr []int, i, n int) {
	//完全二叉树的性质
	for k := 2*i + 1; k <= n; k = 2*k + 1 {
		if k < n && arr[k] < arr[k+1] {
			//找出孩子节点中最大值
			k++
		}
		if arr[k] > arr[i] {
			//孩子节点大于根节点 交换
			arr[k], arr[i] = arr[i], arr[k]
			i = k
		} else {
			break
		}
	}
}

归并排序

//MergeSort O(nlogn) 稳定
func MergeSort(arr []int) {
	n := len(arr)
	temp := make([]int, n)
	mSort(arr, 0, n-1, temp)

}
func mSort(arr []int, left, right int, temp []int) {
	if left < right {
		mid := left + (right-left)/2
		mSort(arr, left, mid, temp)
		mSort(arr, mid+1, right, temp)

		if arr[mid] > arr[mid+1] {
            // 优化  只有当归并的两个序列中 左边的最大值大于右边的最小值才进行merge
			merge(arr, left, mid, right, temp)
		}
	}
}

//merge 合并
func merge(arr []int, left int, mid int, right int, temp []int) {
	i := left
	j := mid + 1
	t := 0
	for i <= mid && j <= right {
		if arr[i] <= arr[j] {
			temp[t] = arr[i]
			i++
		} else {
			temp[t] = arr[j]
			j++
		}
		t++
	}
	for i <= mid {
		temp[t] = arr[i]
		t++
		i++
	}
	for j <= right {
		temp[t] = arr[j]
		t++
		j++
	}
	t = 0
	for left <= right {
		arr[left] = temp[t]
		left++
		t++
	}
}

快速排序

//QuickSort O(nlogn) 最坏(O(n2))  不稳定
func QuickSort(arr []int) {
	Quick(arr, 0, len(arr)-1)
}

func Quick(arr []int, left int, right int) {
    if left >= right{
        return
    }
    i,j,key := left,right,arr[left]
    //选择最左元素为基准元素
	// 在数组有序或选择到的元素为数组最大或最小值时 快排两个序列中有一个序列只有一个元素 快排退化为O(n2)
	//可通过选择最左最右中间三数比较选择基准元素
    for i<j{
        for i<j && arr[j]>key{
            j--
        }
        if i <j{
            arr[i]=arr[j]
            i++
        }        
        for i<j && arr[i]<key{
            j++
        }
        if i <j{
            arr[j]=arr[i]
            j--
        }
    }
    arr[i]=key
    Quick(arr,left,i-1)
    Quick(arr,i+1,right)
}

//非比较排序算法 不受比较型排序算法 O(nlogn)的下限约束

//BucketSort 划分k个区间 将区间内的数据放入对应桶内 再对桶内数据进行排序

//(桶的个数接近n时 时间复杂度为O(n) 空间换时间) 适合用于数据量较大 数据范围确定且较小且数据均匀分布

//CountSort 特殊的桶排序 桶的个数为max-min+1 需要先遍历一遍数组确认最大值和最小值 统计元素出现次数

/CountSort  特殊的桶排序 桶的个数为max-min+1  需要先遍历一遍数组确认最大值和最小值
func CountSort(arr []int)[]int{
	max :=arr[0]
	for i:=1;i<len(arr);i++{
		if max < arr[i]{
			max = arr[i]
		}
	}
	tmp := make([]int,max+1)
	for i:=0; i<len(arr);i++{
		tmp[arr[i]]++
	}
	k:=0
	for i,v := range tmp{
		for j:=1;j<=v;j++{
			arr[k]=i
			k++
		}
	}
	return arr
}

//RadixSort 基数排序

func RadixSort(data []int) []int {
		if len(data) < 2 {
			return data
		}
		max := data[0]
		dataLen := len(data)
		for i := 1; i < dataLen; i++ {
			if data[i] > max {
				max = data[i]
			}
		}
		// 计算最大值的位数
		maxDigit := 0
		for max > 0 {
			max = max/10
			maxDigit++
		}
		// 定义每一轮的除数，1,10,100...
		divisor := 1;
		// 定义了10个桶，为了防止每一位都一样所以将每个桶的长度设为最大,与原数组大小相同
		bucket := [10][10]int{{0}}
		// 统计每个桶中实际存放的元素个数
		count := [10]int{0}
		// 获取元素中对应位上的数字，即装入那个桶
		var digit int
		// 经过maxDigit+1次装通操作，排序完成
		for i := 1; i <= maxDigit; i++ {
			for j := 0; j < dataLen; j++ {
				tmp := data[j]
				digit = (tmp / divisor) % 10
				bucket[digit][count[digit]] = tmp
				count[digit]++
			}
			// 被排序数组的下标
			k := 0
			// 从0到9号桶按照顺序取出
			for b := 0; b < 10; b++ {
				if count[b] == 0 {
					continue
				}
				for c := 0; c < count[b]; c++ {
					data[k] = bucket[b][c]
					k++
				}
				count[b] = 0
			}
			divisor = divisor * 10
		}
		return data
	}