洛谷 P1876 开灯

解法：
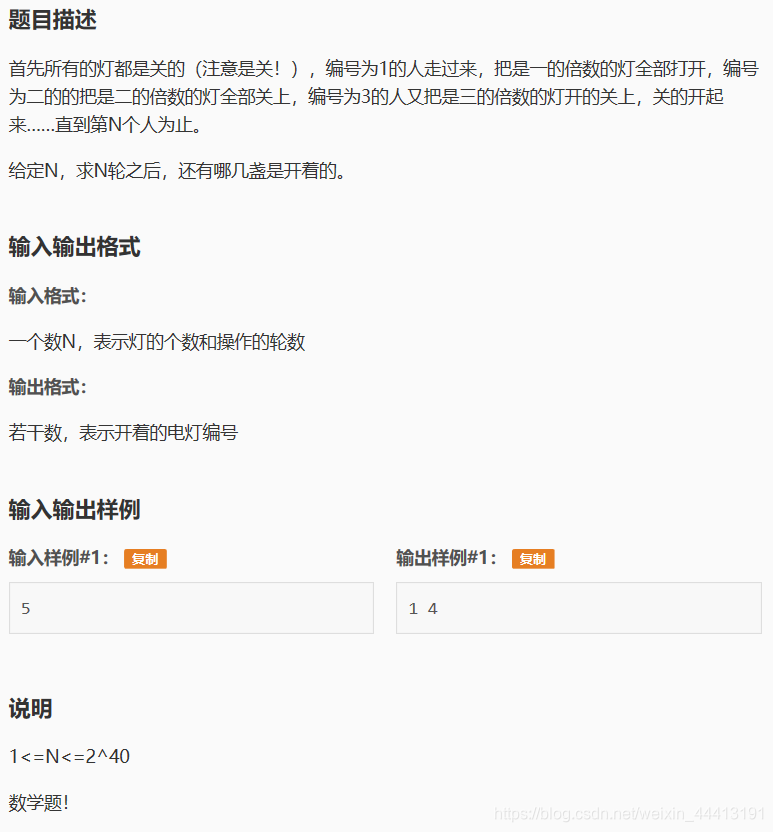
首先要知道，当一个数因数的个数为奇数时，灯是亮的
一个非完全平方数，因数肯定为偶数 例：8:（1,2,4,8）
一个完全平方数，因数肯定为奇数 例：9:（1,3,9）
其实简单来说非完全平方数的每一个因数都可以跟一个不等自己的数相乘得到这个非完全平方数（1,8;2,4）；所以因数一定是偶数
完全平方数其中一个因数乘自己可得到这个完全平方数（19，33）；所以因数一定是奇数；

#include<bits/stdc++.h>
using namespace std;
int main()
{
   
   
 int n,i; cin