洛谷 P4467 [SCOI2007]k短路

最新推荐文章于 2021-04-17 16:08:14 发布

原创

最新推荐文章于 2021-04-17 16:08:14 发布 · 570 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #洛谷 #c++ #图论

本文介绍了洛谷P4467题目的解题策略，重点聚焦于使用A*算法寻找第k个最短路径。通过A*算法的特性，当目标状态第一次被取出时即可得到最优解。为了实现启发式搜索，文章应用了SPFA+SLF+LLL组合来反向计算图的最短路径。

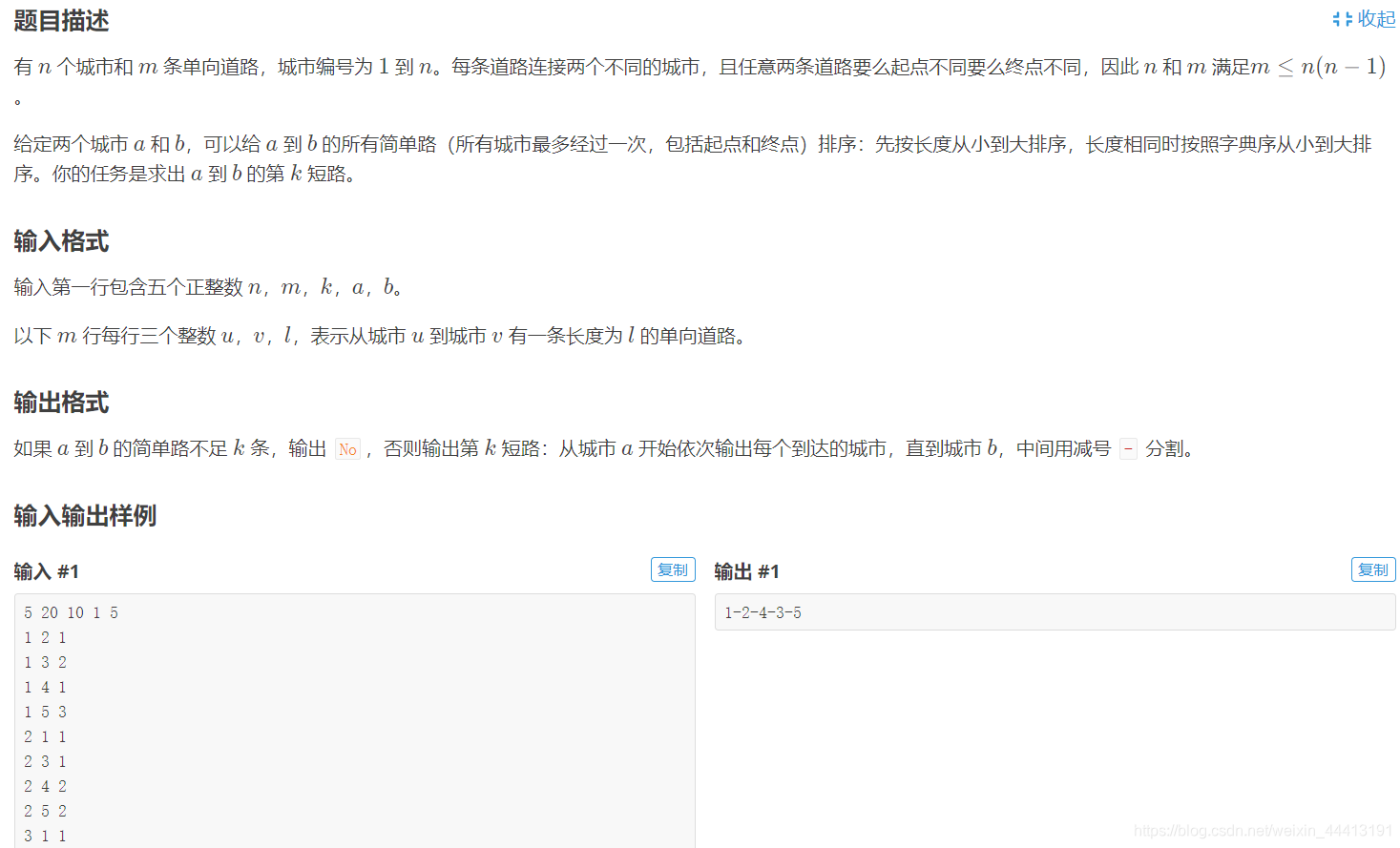
在这里插入图片描述
具体题目见洛谷 P4467

方法一：A*

思路：A* 算法目标状态第一次被取出时即为最优解，根据这个特点，我们只需要取出第 k 个目标状态就是答案。

又因为 A* 算法的估值尽量与正确值相似且必须 $\leq$ 正确值的要求。这里使用 SPFA+SLF+LLL 反向计算最短路径作为启发函数。

#include<bits/stdc++.h>
using namespace std;
const int maxn = 205;
int n, m, k, a, b, sum;
vector<pair<int, int> >E1[maxn];//反图，first为边终点，second为边权
vector<pair<int, int> >E2[maxn];//正图
int d[maxn];//维护每个点到终点的距离
bool vis[maxn];
struct node {
   
   
	int now, w, guess;//边起点、边权、估值
	string route;  //用string存路径方便处理
	//构造函数方便初始化
	node(int now, int w, int guess, string route) : now(now), w(w), guess(guess), route(route) {
   
   	}
	bool operator<(const node& a)const {
   
   //要按照题目要求进行运算符重载
		if (w + d[now] != a.w + d[a.now])