最小生成树

最小生成树

最小生成树（Minimum spanning trees），对于一个连通无向图G=(V, E)（V为节点集合，E为边集合）， 找G中的一个无环子集 $T\in E$ ，使之能够将所有的节点连接起来，又具有最小的权重，即使得$w(T)={\sum }_{(u,v)\in T}w(u,v)$的值最小（注：最小生成树不一定唯一）

1. MST性质

一些基本的概念：

• 安全边：在每遍循环之前，A是某棵最小生成树的一个子集，每一次我们选择一条边 (u, v) 加入集合A，使得**$A\cup (u,v)$仍是某棵最小生成树的子集**，则 (u, v) 就成为集合A的安全边。（求最小生成树就是不断的加入安全边即可）
• 横跨切割：如果一条边$(u,v)\in E$的一个端点在集合S中，另一个端点在集合V-S中，则称该条边横跨切割(S, V-S)
• 尊重：如果边集A中不存在横跨该切割的边，则称该切割尊重集合A
• 轻量级边：在横跨一个切割的所有边中，权重最小的边称为轻量级边

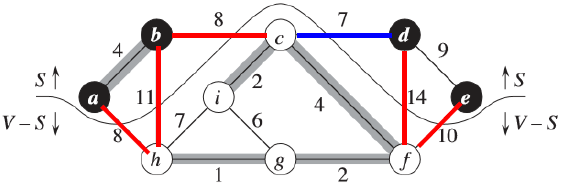
举个栗子：

• 横跨切割 (S, V-S) 的边：(b, c), (c, d), (b, h), (d, f), (a, h), (e, f)
• 轻量级边：(c, d) 是唯一的轻量级边，权重为7
• 尊重：设集合A = {(a, b), (c, i), (c, f), (f, g), (g, h)} （途中的灰色边），则该切割 (S, V - S) 不存在横跨A的边，故切割 (S, V - S)尊重集合A

MST性质：设G = (V, E) 是一个在边E上定义了实数值权重函数w的连通无向图。设集合A为E的一个子集，且A中包含在图G的某棵最小生成树中，设 (S, V - S) 是图G中尊重集合A的任意一个切割，又设(u, v)是横跨切割 (S, V - S)的一条轻量级边，那么边(u, v)对于集合A是安全的。（证明略，可以自行参考算法导论P364）

根据MST性质，我们就能得到最小生成树的算法了

2. 具体实现

kruskal和prim算法都是GENERIC-MST算法的具体实现，二者都是通过一个具体的规则来确定GENERIC-MST算法中的第三行所描述的安全边。两个算法的时间复杂度均为$O(ElgV)$，详细证明参考算法导论P366和P369，算法题链接

2.1 kruskal

算法描述：

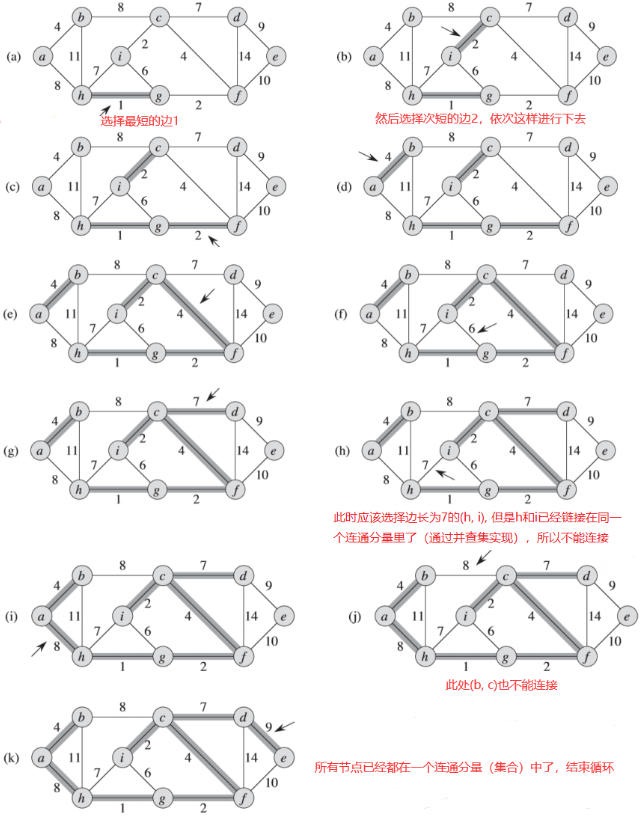
集合A始终是一个森林，开始时，其节点集就是G的节点集，并且A是所有单节点树构成的森林。之后每次加入到集合A中的安全边是连接A的两个不同连通分量的权重最小的边。

举个栗子：

详细代码：

kruskal其实主要就是用到并查集，并查集链接

#include<iostream>
#include<algorithm>
using namespace std;
#define N 5500
#define M 2100
int parent[N], depth[N];
// 并查集模板
void init(int n) {
	for (int i = 0; i <= n; i++) {
		parent[i] = i;
		depth[i] = 1;
	}
}
int find(int i) {
	while (i != parent[i]) {
		parent[i] = parent[parent[i]];
		i = parent[i];
	}
	return i;
}
inline bool connected(int p, int q) {
	p = find(p);
	q = find(q);
	return p == q;
}
void unionNode(int p, int q) {
	p = find(p);
	q = find(q);
	if (p == q) {// 根节点相同，无需合并
		return;
	}
	else if (depth[p] > depth[q]) {
		parent[q] = p;
	}
	else if (depth[p] < depth[q]) {
		parent[p] = q;
	}
	else {
		parent[q] = p;
		depth[p]++;
	}
}
// 查并集模板

struct edge
{
	int u, v, w;
	friend bool operator <(edge e1, edge e2) {
		return e1.w < e2.w;
	}
} arr[M];
int main() {
	int n, m, ans = 0, num = 0;
	cin >> n >> m;
	init(n);
	for (int i = 1; i <= m; i++) {
		cin >> arr[i].u >> arr[i].v >> arr[i].w;
	}
	sort(arr + 1, arr + m + 1);
	for (int i = 1; i <= m; i++) {
		if (connected(arr[i].u, arr[i].v))
			continue;
		ans += arr[i].w;
		num++;
		unionNode(arr[i].u, arr[i].v);
	}
	if (num < n - 1)
		cout << "orz" << endl;
	else
		cout << ans << endl;
	return 0;
}

2.2 prim

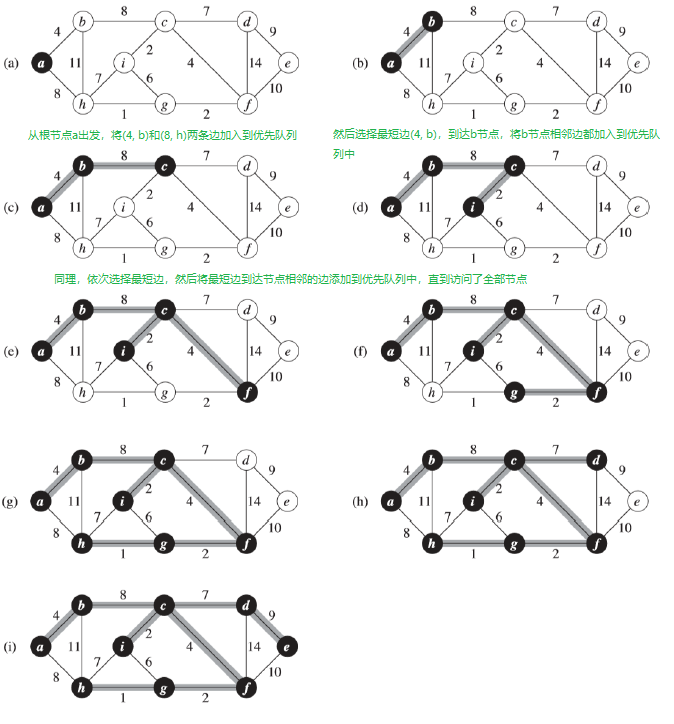
算法描述：

举个栗子：

详细代码实现：

#include<iostream>
#include<list>
#include<map>
#include<queue>
#include<string.h>
using namespace std;
#define N 5100
list<pair<int, int> > head[N];
// 记录以每一个节点为首的边的链表
// 例如 head[u] 表示通过u节点的边的链表, first表示边的权重, second表示相邻节点
int vis[N];
// 记录每个节点是否被访问, 0未访问, 1已访问
void prim(int n) {
	int u, w, cnt = 0;
	long long ans = 0;
	priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > > q;
	// 优先队列, first表示边的权重, second表示到达的节点
	q.push(make_pair(0, 1));
	// 从1号节点出发开始寻找最小生成树
	while (!q.empty() && cnt < n) {
		// 取得优先队列中权重最小的边
		w = q.top().first;
		u = q.top().second;
		q.pop();
		if (vis[u] != 0)	// 如果节点已经在最小生成树中，跳过
			continue;
		vis[u] = 1;
		cnt++;
		ans += w;
		// 将到达节点相邻的未访问节点的边添加到优先队列中
		for (auto it = head[u].begin(); it != head[u].end(); it++) {
			if (vis[it->second] == 0) 
				q.push(make_pair(it->first, it->second));
		}
	}
	if (cnt < n)
		cout << "orz" << endl;
	else
		cout << ans << endl;
}
int main() {
	memset(vis, 0, sizeof(vis));
	int n, m, u, v, w;
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		cin >> u >> v >> w;
		head[u].push_back(make_pair(w, v));
		head[v].push_back(make_pair(w, u));
	}
	prim(n);
}