梯度下降详解

概论

梯度下降（Gradient Descent GD）是用来寻求损失函数（loss function）最小化的方法，最为常用随机梯度下降（stochastic gradient descent）SGD，几乎可以解决除了决策树之外所有算法的损失函数最小化问题。

比较通俗的例子是一个人站在山顶，为了尽快下山，这个人需要寻找当前位置最为陡峭的方向往下走。

另一个更好的例子是山泉流入山谷的过程。

1. 水本身是受到重力影响的，水流就会沿着当前最为陡峭的方向流动，甚至是垂直流下。（梯度下降）
2. 水流在某些地方，会分流，因为多个方向具有同样的陡峭度（梯度）。（可能有多个解）
3. 遇到洼地，水流可能形成湖泊，而不再往山下流。（局部最优，不是全局最优）

理论基础

了解梯度下降，需要数学中微积分的相关知识。包括导数、微分、偏导数、梯度。

导数和微分

导数的几何意义是该函数曲线在这一点上的切线斜率。函数$y=f(x)$在$x_0$点的导数$f^{\prime }(x_0)$的几何意义：表示函数曲线在点$P_0(x_0,f(x_0))$处的切线的斜率。

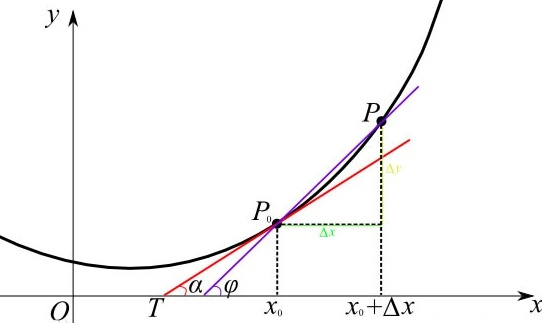
导数的计算，几乎就是所有深度学习中优化算法的关键步骤。深度学习中通常选取的损失函数，是对于模型参数可微的。

简而言之，对于每一个参数，如果我们对这个参数增加或者减少一个无穷小的量，我们可以知道损失会以多快的速度增加和减少。

假设我们有一个函数$f:{\mathbb{R}}^n\to \mathbb{R}$，其输入和输出都是标量。如果$f$的导数存在，这个极限被定义为

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}.$$

如果$f^{\prime }(a)$存在，则称$f$在$a$处是可微（differentiable）的。如果$f$在一个区间内的每个数上都是可微的，则此函数在此区间中是可微的。
我们可以将 导数$f^{\prime }(x)$解释为$f(x)$相对于$x$的瞬时（instantaneous）变化率。所谓的瞬时变化率是基于$x$中的变化$h$，且$h$接近$0$。

偏导数

前面我们只描述了一个变量的函数的微分。在深度学习中，目标函数通常依赖于许多变量。因此，我们需要将微分的思想推广到多元函数（multivariate function）上。

偏导数的几何意义

设$y=f(x_1,x_2,\dots ,x_n)$是一个具有$n$个变量的函数。$y$关于第$i$个参数$x_i$的偏导数（partial derivative）为：

$$\frac{\partial y}{\partial x_i}=\underset{h\to 0}{\lim }\frac{f(x_1,\dots ,x_{i-1},x_i+h,x_{i+1},\dots ,x_n)-f(x_1,\dots ,x_i,\dots ,x_n)}{h}.$$

为了计算$\frac{\partial y}{\partial x_i}$，我们可以简单地将$x_1,\dots ,x_{i-1},x_{i+1},\dots ,x_n$看作常数，并计算$y$关于$x_i$的导数。对于偏导数的表示，以下是等价的：

$$\frac{\partial y}{\partial x_i}=\frac{\partial f}{\partial x_i}=f_{x_i}=f_i=D_{i}f=D_{x_i}f.$$

梯度

我们可以连结一个多元函数对其所有变量的偏导数，以得到该函数的梯度（gradient）向量。具体而言，设函数$f:{\mathbb{R}}^n\to \mathbb{R}$的输入是一个$n$维向量$\mathbf{x}=[x_1,x_2,\dots ,x_n{]}^{\top }$，并且输出是一个标量。函数$f(\mathbf{x})$相对于$\mathbf{x}$的梯度是一个包含$n$个偏导数的向量:

$${\nabla }_{\mathbf{x}}f(\mathbf{x})=[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\dots ,\frac{\partial f(\mathbf{x})}{\partial x_n}{]}^{\top }$$

其中${\nabla }_{\mathbf{x}}f(\mathbf{x})$通常在没有歧义时被$\nabla f(\mathbf{x})$取代。

假设$\mathbf{x}$为$n$维向量，在微分多元函数时经常使用以下规则:

• 对于所有$\mathbf{A}\in {\mathbb{R}}^{m\times n}$，都有${\nabla }_{\mathbf{x}}\mathbf{A}\mathbf{x}={\mathbf{A}}^{\top }$
• 对于所有$\mathbf{A}\in {\mathbb{R}}^{n\times m}$，都有${\nabla }_{\mathbf{x}}{\mathbf{x}}^{\top }\mathbf{A}=\mathbf{A}$
• 对于所有$\mathbf{A}\in {\mathbb{R}}^{n\times n}$，都有${\nabla }_{\mathbf{x}}{\mathbf{x}}^{\top }\mathbf{A}\mathbf{x}=(\mathbf{A}+{\mathbf{A}}^{\top })\mathbf{x}$
• ${\nabla }_{\mathbf{x}}\Vert \mathbf{x}{\Vert }^2={\nabla }_{\mathbf{x}}{\mathbf{x}}^{\top }\mathbf{x}=2\mathbf{x}$

同样，对于任何矩阵$\mathbf{X}$，都有${\nabla }_{\mathbf{X}}\Vert \mathbf{X}{\Vert }_F^2=2\mathbf{X}$。正如我们之后将看到的，梯度对于设计深度学习中的优化算法有很大用处。

链式法则

然而，上面方法可能很难找到梯度。这是因为在深度学习中，多元函数通常是复合（composite）的，所以我们可能没法应用上述任何规则来微分这些函数。幸运的是，链式法则使我们能够微分复合函数。

让我们先考虑单变量函数。假设函数$y=f(u)$和$u=g(x)$都是可微的，根据链式法则：

$$\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}.$$

现在让我们把注意力转向一个更一般的场景，即函数具有任意数量的变量的情况。假设可微分函数$y$有变量$u_1,u_2,\dots ,u_m$，其中每个可微分函数$u_i$都有变量$x_1,x_2,\dots ,x_n$。注意，$y$是$x_1,x_2，\dots ,x_n$的函数。对于任意$i=1,2,\dots ,n$，链式法则给出：

$$\frac{dy}{d{x}_i}=\frac{dy}{d{u}_1}\frac{d{u}_1}{d{x}_i}+\frac{dy}{d{u}_2}\frac{d{u}_2}{d{x}_i}+\cdots +\frac{dy}{d{u}_m}\frac{d{u}_m}{d{x}_i}$$

梯度下降

梯度下降很少直接用于深度学习中，但它是很多算法(如随机梯度下降)的基础。

数学定义

梯度下降的数学公式：

$${\theta }_{n+1}={\theta }_n-\eta \cdot \nabla J(\theta )\text{\hspace{1em}(1)}$$

其中：

• ${\theta }_{n+1}$：下一个值；
• ${\theta }_n$：当前值；
• $-$：减号，梯度的反向；
• $\eta$：学习率或步长，控制每一步走的距离，不要太快以免错过了最佳景点，不要太慢以免时间太长；
• $\nabla$：梯度，函数当前位置的最快上升点；
• $J(\theta )$：函数。

梯度下降的三要素

1. 当前点；
2. 方向；
3. 步长。

为什么说是“梯度下降”？

“梯度下降”包含了两层含义：

1. 梯度：函数当前位置的最快上升点；
2. 下降：与导数相反的方向，用数学语言描述就是那个减号。

亦即与上升相反的方向运动，就是下降。

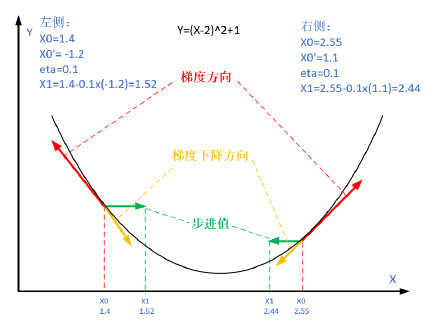
一维梯度下降

为什么梯度下降算法可以优化目标函数？一维中的梯度下降给我们很好的启发。考虑一类连续可微实值函数$f:\mathbb{R}\to \mathbb{R}$，利用泰勒展开，我们可以得到

$$f(x+ϵ)=f(x)+ϵf^{\prime }(x)+\mathcal{O}({ϵ}^2).$$

注：二阶段泰勒展开

$$f(x)=f(x_0)+f^{\prime }(x_0)(x-x_0)+\frac{f^{\prime \prime }(x_0)}{2}(x-x_0{)}^2+O(|x-x_0{|}^3).$$

即在一阶近似中，$f(x+ϵ)$可通过$x$处的函数值$f(x)$和一阶导数$f^{\prime }(x)$得出。我们可以假设在负梯度方向上移动的$ϵ$会减少$f$。为了简单起见，我们选择固定步长$\eta >0$，然后取$ϵ=-\eta f^{\prime }(x)$。将其代入泰勒展开式我们可以得到

$$f(x-\eta f^{\prime }(x))=f(x)-\eta f^{\prime 2}(x)+\mathcal{O}({\eta }^2{f}^{\prime 2}(x)).$$

如果其导数$f^{\prime }(x)\ne 0$没有消失，我们就能继续展开，这是因为$\eta f^{\prime 2}(x)>0$。此外，我们总是可以令$\eta$小到足以使高阶项变得不相关。因此，

$$f(x-\eta f^{\prime }(x))⪅f(x).$$

这意味着，如果我们使用

$$x\leftarrow x-\eta f^{\prime }(x)$$

来迭代$x$，函数$f(x)$的值可能会下降。因此，在梯度下降中，我们首先选择初始值$x$和常数$\eta >0$，然后使用它们连续迭代$x$，直到停止条件达成。例如，当梯度$|f^{\prime }(x)|$的幅度足够小或迭代次数达到某个值时。

学习率

学习率（learning rate）决定目标函数能否收敛到局部最小值，以及何时收敛到最小值。学习率$\eta$可由算法设计者设置。请注意，如果我们使用的学习率太小，将导致$x$的更新非常缓慢，需要更多的迭代。

相反，如果我们使用过高的学习率，$\left|\eta f^{\prime }(x)\right|$对于一阶泰勒展开式可能太大。也就是说，$\mathcal{O}({\eta }^2{f}^{\prime 2}(x))$可能变得显著了。在这种情况下，$x$的迭代不能保证降低$f(x)$的值。

局部最小

为了演示非凸函数的梯度下降，考虑函数$f(x)=x\cdot \cos (cx)$，其中$c$为某常数。这个函数有无穷多个局部最小值。根据我们选择的学习率，我们最终可能只会得到许多解的一个。下面的例子说明了（不切实际的）高学习率如何导致较差的局部最小值。

多元梯度下降

现在我们对单变量的情况有了更好的理解，让我们考虑一下$\mathbf{x}=[x_1,x_2,\dots ,x_d{]}^{\top }$的情况。即目标函数$f:{\mathbb{R}}^d\to \mathbb{R}$将向量映射成标量。相应地，它的梯度也是多元的：它是一个由$d$个偏导数组成的向量：

$$\nabla f(\mathbf{x})=[\frac{\partial f(\mathbf{x})}{\partial x_1},\frac{\partial f(\mathbf{x})}{\partial x_2},\dots ,\frac{\partial f(\mathbf{x})}{\partial x_d}{]}^{\top }.$$

梯度中的每个偏导数元素$\partial f(\mathbf{x})/\partial x_i$代表了当输入$x_i$时$f$在$\mathbf{x}$处的变化率。和先前单变量的情况一样，我们可以对多变量函数使用相应的泰勒近似来思考。具体来说，

$$f(\mathbf{x}+\mathbf{ϵ})=f(\mathbf{x})+{\mathbf{ϵ}}^{\top }\nabla f(\mathbf{x})+\mathcal{O}(\Vert \mathbf{ϵ}{\Vert }^2).$$

换句话说，在$\mathbf{ϵ}$的二阶项中，最陡下降的方向由负梯度$-\nabla f(\mathbf{x})$得出。
选择合适的学习率$\eta >0$来生成典型的梯度下降算法：

$$\mathbf{x}\leftarrow \mathbf{x}-\eta \nabla f(\mathbf{x}).$$

总结

梯度下降是深度学习中基础的理论，希望整理的资料能对梯度下降有一个整体的认识。

参考资料

泰勒展开

什么是梯度下降

动手学深度学习