计组实验4 控制冒险与分支预测

前言

上一篇博客：计组实验3 mips冒险之流水线冒险

摸了半个月了。。。咕咕咕 今天来写计组实验 4

这个实验非常简单，就是有点难。

这个实验比较容易算错，或者是被模拟器出人意料的结果搞的神神叨叨的，所以今天来记录并且详细分析该实验。

注：请务必阅读本文的【阻塞周期计算方法】部分，这部分是结论！看了就容易看懂实验中周期的计算。

实验内容

按照下面的实验步骤及说明，完成相关操作记录实验过程的截图：

1. 首先，给出一段矩阵乘法的代码，通过开启BTB功能对其进行优化，并且观察流水线的细节，解释BTB在其中所起的作用；
2. 其次，自行设计一段使得即使开启了BTB也无效的代码。
3. 第三，使用循环展开的方法，观察流水因分支停顿的次数减少的现象，并对比采用BTB结构时流水因分支而停顿的次数。

（选做：在x86系统上编写C语言的矩阵乘法代码，用perf观察分支预测失败次数，分析其次数是否与你所学知识吻合。再编写前面第二部使用的令分支预测失败的代码，验证x86是否能正确预测，并尝试做解释）

背景知识

在遇到跳转语句的时候，我们往往需要等到MEM阶段才能确定这条指令是否跳转（通过硬件的优化，可以极大的缩短分支的延迟，将分支执行提前到ID阶段，这样就能够将分支预测错误代价减小到只有一条指令）

这种为了确保预取正确指令而导致的延迟叫控制冒险（分支冒险）。为了降低控制冒险所带来的性能损失，一般采用分支预测技术。

分支预测技术

分支预测技术包含编译时进行的静态分支预测，和执行时进行的动态分支预测。这里，我们着重介绍动态分支预测中的BTB（Branch Target Buffer）技术。

BTB即为分支目标缓冲器，它将分支指令（对应的指令地址）放到一个缓冲区中保存起来，当下次再遇到相同的指令（跳转判定）时，它将执行和上次一样的跳转（分支或不分支）预测。

一种可行的BTB结构示意图如下：

在采用了BTB之后，在流水线各个阶段所进行的相关操作如下：

注意，为了填写或者删除BTB，需要 2 个周期。

这句话非常重要，对于我们的后续计算代码的阻塞周期数目十分重要。！！BTB分支的建立和错误，都会占用 2 个周期。

阻塞周期计算方法⭐

相信很多童鞋和我一样，在初次执行循环代码时，都会对阻塞的周期数目感到非常疑惑。

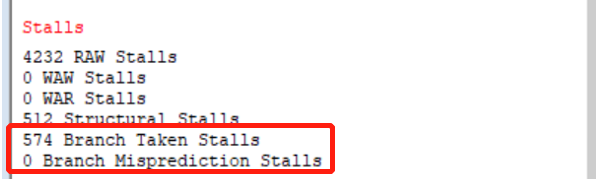
于是下面直接给出我总结的阻塞周期数目规律。以本实验的循环代码框架为例（即beq放在循环最后面，判断是否需要跳转回 loop 标号）

不开启 BTB

不开起 BTB 的情况下，mips 默认预测恒不跳转，一个 n 次的循环，会有 n-1 次 Branch Taken Stall，因为除了最后一次退出循环，beq 预测正确，其他的时候，beq 都是预测错误。而每个 Branch Taken Stall 阻塞一个周期

所以最终阻塞的周期数 = (n-1) * 1 = n-1 个周期

开启 BTB

开启 BTB 的情况下，一个 n 次的循环，会有 1 次 Branch Taken Stalls 和 1 次 Branch Misprediction Stalls

因为第一次进入循环，BTB 还未建立，发生 1 次 Branch Taken Stalls

此外，最后一次退出循环时的 beq，因为我们之前 BTB 都是预测它要跳转，于是最后一次出现预测失误，需要清除 BTB，发生一次 Branch Misprediction Stalls

不论 Branch Misprediction Stalls 和 Branch Misprediction Stalls，都需要花费 2 个周期去整改 BTB，所以最终阻塞的周期数 = 2

part 1 矩阵乘法与优化

在这一阶段，我们首先给出矩阵乘法的例子，接着将流水线设置为不带BTB功能（configure->enable branch target buffer）直接运行，观察结果进行记录；

然后，再开启BTB功能再次运行，观察实验结果。将两次的实验结果进行对比，观察BTB是否起作用，如果有效果则进一步观察流水线执行细节并且解释BTB起作用原因。

矩阵乘法的代码如下：