最小体力消耗路径（并查集 / LeetCode ）

最新推荐文章于 2024-05-26 14:22:34 发布

你喜欢梅西吗

最新推荐文章于 2024-05-26 14:22:34 发布

阅读量231

点赞数

CC 4.0 BY-SA版权

分类专栏：刷题文章标签： leetcode 贪心算法图论算法

本文链接：https://blog.youkuaiyun.com/weixin_44164489/article/details/113376596

刷题专栏收录该内容

129 篇文章

订阅专栏

本文介绍如何利用并查集算法计算从二维地图左上角到右下角的最小体力消耗路径，通过计算高度差绝对值最大边来优化路径。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目链接

题目描述

你准备参加一场远足活动。给你一个二维 rows x columns 的地图 heights ，其中 heights[row][col] 表示格子 (row, col) 的高度。一开始你在最左上角的格子 (0, 0) ，且你希望去最右下角的格子 (rows-1, columns-1) （注意下标从 0 开始编号）。你每次可以往上，下，左，右四个方向之一移动，你想要找到耗费体力最小的一条路径。

一条路径耗费的体力值是路径上相邻格子之间高度差绝对值的最大值决定的。

请你返回从左上角走到右下角的最小体力消耗值。

示例 1：
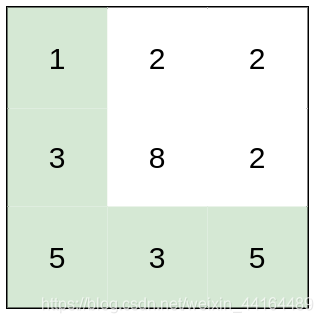
在这里插入图片描述

输入：heights = [[1,2,2],[3,8,2],[5,3,5]]
输出：2
解释：路径 [1,3,5,3,5] 连续格子的差值绝对值最大为 2 。
这条路径比路径 [1,2,2,2,5] 更优，因为另一条路径差值最大值为 3 。

提示：

rows == heights.length
columns == heights[i].length
1 <= rows, columns <= 100
1 <= heights[i][j] <= 10^6

思路

使用并查集实现，把所有的边按照高度差绝对值从小到大排序后，逐条边加入到并查集中，一旦加入某条边后左上角和右下角成功连通（即二者的parent一样），则该边即答案。

代码如下：

class Solution {
public:
    int find(vector<int> &parent,int n){
        if(parent[n]==n)
            return n;
        parent[n]=find(parent,parent[n]);
        return parent[n];
    }
    int minimumEffortPath(vector<vector<int>>& heights) {
        int row=heights.size(),col=heights[0].size(),len=row*col;
        if(len==1)
            return 0;
        vector<int> parent(len);
        vector<int> rank(len,0);
        for(int i=0;i<len;i++)
            parent[i]=i;
        vector<tuple<int,int,int>> edges;
        for(int i=0;i<row;i++)
        for(int j=0;j<col;j++){
            if(i<row-1)
                edges.emplace_back(tuple<int,int,int>(i*col+j,i*col+j+col,abs(heights[i][j]-heights[i+1][j])));
            if(j<col-1)
                edges.emplace_back(tuple<int,int,int>(i*col+j,i*col+j+1,abs(heights[i][j]-heights[i][j+1])));
        }
        sort(edges.begin(),edges.end(),[&](tuple<int,int,int> a,tuple<int,int,int> b){
            return get<2>(a)<get<2>(b);
        });
        for(auto edge:edges){
            int node1=get<0>(edge),node2=get<1>(edge),p1=find(parent,node1),p2=find(parent,node2);
            if(p1!=p2){
                if(rank[p1]==rank[p2]){
                    parent[p1]=p2;
                    rank[p2]++;
                }
                else if(rank[p1]>rank[p2])
                    parent[p2]=p1;
                else
                    parent[p1]=p2;
            }
            if(find(parent,0)==find(parent,len-1))
                return get<2>(edge);
        }
        return 0;
    }
};