408数据结构 第三章 栈和队列

第三章 栈和队列

不可以随便读取栈或队列中间的某个数据

3.1 栈

性质

• 后进先出LIFO
• n个不同元素进栈，出栈元素不同排列的个数为$$\frac{1}{n+1}{C}_{2n}^n$$

顺序栈的基本运算

注意：

初始化 S.top = -1

//初始化
void InitStack(SqStack &S)
{
    S.top = -1;
}
//判断栈空
bool StackEmpty(SqStack S)
{
    if (S.top == -1)
        return true;
    else 
        return false;
}
//入栈
bool Push(SqStack &S, int x)
{
    if (S.top == MaxSize-1)
        return false;
    S.data[++S.top] = x;
    return true;
}
//出栈
bool Pop(SqStack &S, int &x)
{
    if (S.top == -1)
        return false;
    x = S.data[S.top--];
    return true;
}
//读栈顶元素
bool GetTop(SqStack S, int &x)
{
    if (S.top == -1)
        return false;
    x = S.data[S.top];
    return true;
}

共享栈

• 为了更有效地利用存储空间，两个栈的空间相互调节，只有在整个存储空间被占满时才发生上溢

链栈

• 一般规定链栈没有头结点

3.2 队列

队列的顺序存储结构

• 循环队列

  • 初始时：Q.front = Q.rear = 0
  • 队首指针进1：Q.front = (Q.front+1)%MaxSize
  • 队尾指针进1：Q.rear = (Q.rear+1)%MaxSize
  • 队列长度：(Q.rear - Q.front + MaxSize)%MaxSize

• 区分队空和队满

  • 牺牲一个单元

    队满：(Q.rear+1)%MaxSize = Q.front

    队空：Q.front = Q.rear

    总个数：(Q.rear - Q.front + MaxSize)%MaxSize

  • 增设Size表示成员数

    队满：Q.size = MaxSize

    队空：Q.size = 0

  • 增设tag（0表示最近进行了删除，1表示插入）

    队满：Q.front = Q.rear && tag = 1

    队空：Q.front = Q.rear && tag = 0

队列的链式存储结构

课本P76

双端队列

• 输出受限的双端队列
• 输入受限的双端队列

3.3 栈和队列的应用

栈在括号匹配中的作用

参见gitee

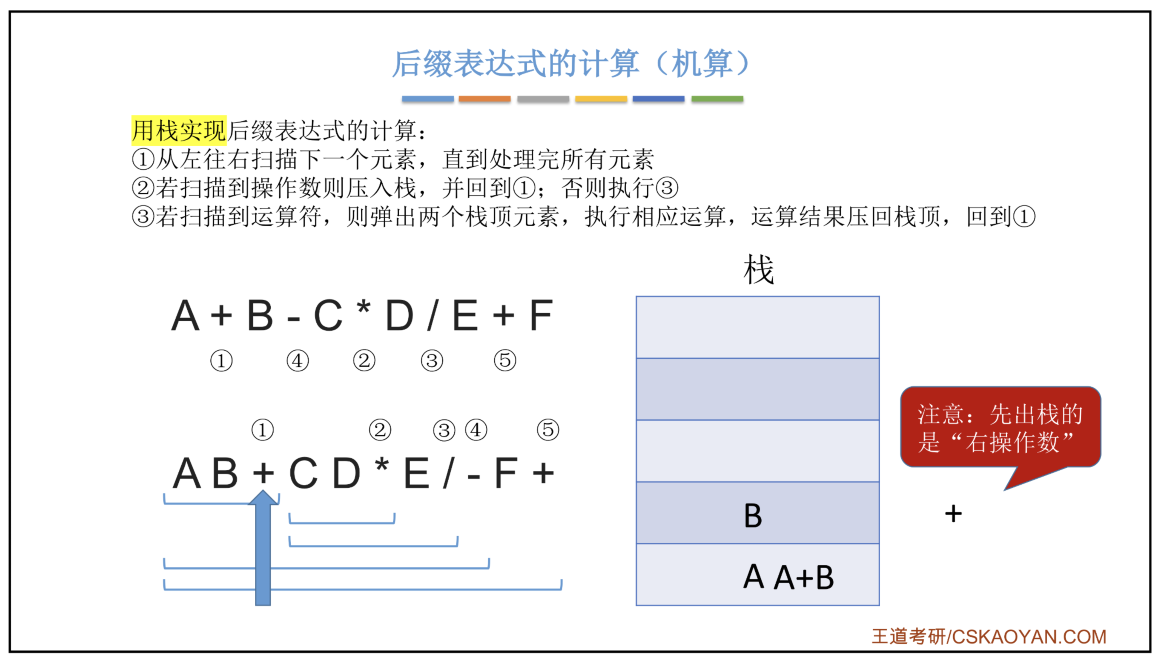
栈在表达式求值中的应用

• 中缀表达式转后缀表达式

• 中缀表达式转前缀表达式

• 利用栈实现前/中/后缀表达式的计算

  
  

栈在递归中的应用

队列在层次遍历中的应用

队列在计算机系统中的应用

• 解决主机与外部设备之间速度不匹配的问题
• 解决由多用户引起的资源竞争问题

3.4 特殊矩阵的压缩存储

1. 数组的存储结构

二维数组的行下标与列下标范围分别为[0,h1]与[0,h2]：

• 行优先：$$LOC(a_{i,j})=LOC(a_{0,0})+[i\ast (h_2+1)+j]\ast L$$
• 列优先：$$LOC(a_{i,j})=LOC(a_{0,0})+[j\ast (h_1+1)+i]\ast L$$

2. 矩阵的压缩存储

A[1…n][1…n]，k表示数组下标，k从0开始

对称矩阵
$$k=\{\begin{array}{l}\frac{i(i-1)}{2}+j-1,i\ge j(下三角区和主对角元素)\\ \frac{j(j-1)}{2}+i-1,i<j(上三角区元素a_{ij}=a_{ji})\end{array}$$
三角矩阵

• 下三角矩阵

$$k=\{\begin{array}{l}\frac{i(i-1)}{2}+j-1,i\ge j(下三角区和主对角元素)\\ \frac{n(n+1)}{2},i<j(上三角区元素)\end{array}$$

• 上三角矩阵

$$k=\{\begin{array}{l}\frac{(i-1)(2n-i+2)}{2}+j-i,i\ge j(上三角区和主对角元素)\\ \frac{n(n+1)}{2},i<j(下三角区元素)\end{array}$$

三对角矩阵
$$k=3(i-1)-1+j-i+2-1=2i+j-3$$
已知k，得到 i, j：
$$\begin{gathered} 3(i-1)-1<k+1\le 3i-1 \\ =>i\ge \frac{k+2}{3} \\ =>i=\lceil \frac{k+2}{3}\rceil \end{gathered}$$

3. 稀疏矩阵

• 矩阵元素个数s $\gg$ 矩阵中非零元素个数t
• 三元组存储：（行标，列标，值）
• 三元组既可以采用数组存储，也可以采用十字链表法存储