基于运动学的横向控制1

最新推荐文章于 2024-09-16 08:00:00 发布

小说家爱学习

最新推荐文章于 2024-09-16 08:00:00 发布

阅读量975

点赞数

本文链接：https://blog.youkuaiyun.com/weixin_44105733/article/details/119844687

版权

周末有空，简单回顾下之前做的横向控制LKA，发现里面还是有一些问题可以去讨论并探究的。LKA就是车辆方向盘由控制器控制，保持在自车车道中间的一种模式，车辆横向控制一般有以下3种方法：

1.基于模型的persuit算法以及stanley算法。

2 .无模型下的pid算法

3.基于模型预测的MPC算法

谈到车辆控制就不得不说两种车辆建模的方式，车辆运动学和车辆动力学，横向控制在这里暂时讨论基于运动学的（动力学的可以参考无人驾驶车辆模型预估控制以及apollo开源5.0控制代码）。

车辆在该坐标系满足： $x\dot{} = vcos\phi$ , $y\dot{} = vsin\phi$ , $\phi \dot{} = v*tan\delta /L$ , 简化该模型到自行车模型，那么在车辆还未运动的情况下，如下图 $tan\delta =L/R$ , 将曲率k带入公式，就可以得到此刻车辆的转角关系式： $\delta = arctan(kL)$

车辆此刻转弯，在该时刻到下一时刻，车辆的后轴从start(x,y)移动到end（x,y）点，通过下一时刻车辆走过的几何路径求得对应的转角 $\delta = arctan(2Lsina/L_{d})$ .

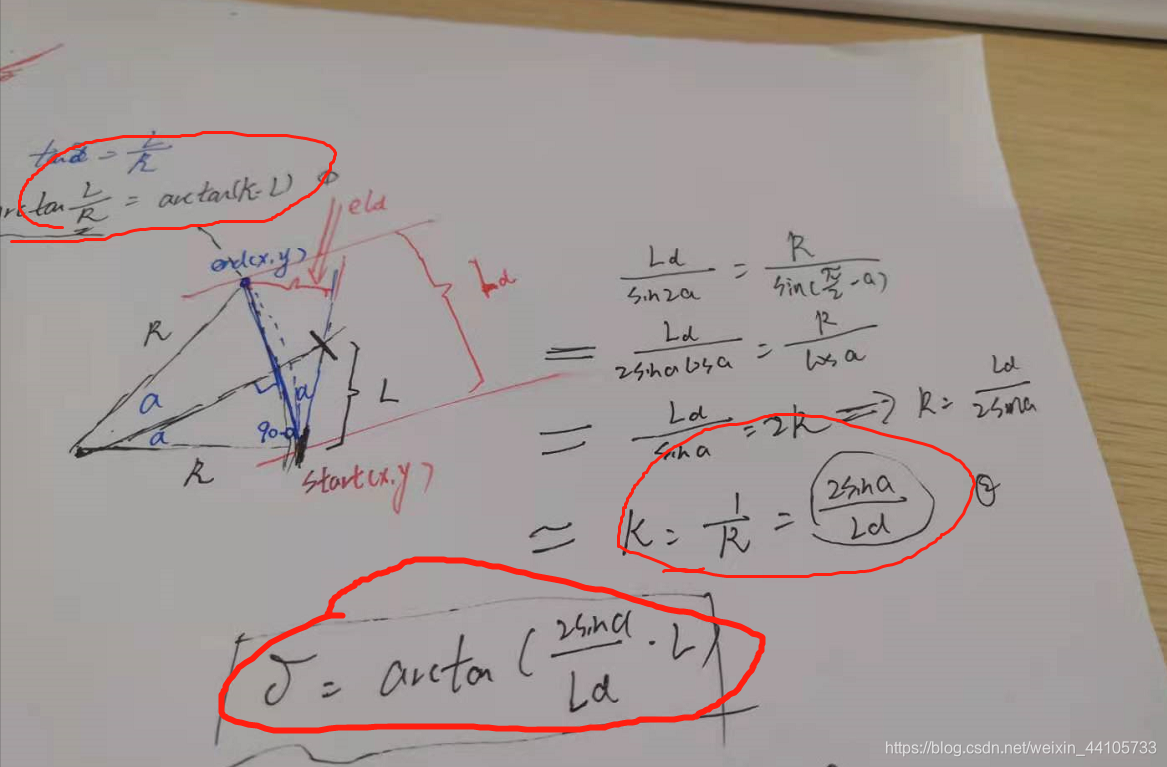
1，这个预瞄的距离 $L_{d}$ 往往和车速成正比，即车速越快，其实我们需要观察的越远。所以公式就可以转化为： $\delta = arctan(2Lsina/mv)$ ，m就是对应的整定系数。当然，有转弯的情况习惯的驾驶情况是减少观察量，以保证转弯安全，那预瞄的距离是否和曲率成反比？

2，关于这个sina的计算，其实我上图已经标注出来了，就是车轮轴向L的延长线和下一时刻end(x,y)的差值除以对应的预瞄距离 $L_{d}$ 。

该算法上没有考虑到跟踪的横向偏差，stanley算法考虑到了这一点，并在05年DARPA Grand Challenge获得第一名。

可以看到同样的转角计算，考虑到了两个方面，第一个方面是trajiectory做点切线平移到前轴中点，与车轴线的偏差 $\theta_{e}$ ，还有一方面车辆此刻和参考轨迹的横向偏差e，图上可以看出几何关系， $\delta _{e} = arctan(e/d)$ , 这里的d很明显和速度v成正比关系，也就是代码测试需要整定的就是这部分的关系，也就是 $\delta = arctan(me/v)+\theta _{e}$ , 到这里第一部分就讲解完了，就是基于实际的模型去分析得到转角的方程去控制。