红黑树 完整原理解析（搜索、插入、删除、黑三角处理），通俗易懂

---

前言

最近做游戏开发，遇到了一个有大量数据存取需要的情况，得用一个容器来装。
首先考虑常用的动态数组，但发现有频繁插入与删除操作，又要维持顺序，显然不合适。
转而考虑链表，又发现有随机存取的需求，所以也不合适。
于是考虑使用一种更加折中，读取，插入，删除速度都还不错的容器 “二叉树”，
这里选择红黑树，其他种类二叉树不考虑使用也不在讨论范围。
由于此前并没有过多的了解过二叉树所以趁此机会顺便学习一下，因为网上难以找到完整的红黑树原理文章，所以特此亲自来写，欢迎指正错误~
这篇文章适合那些想完全没有二叉树基础，并且想自己实现或了解红黑树的人
顺便红黑树长这样：

---

树的基础概念

• 结点

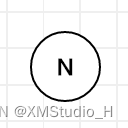
  • 结点是树的基本构成单位，也是单个数据的基本容器，下图是一个结点，用字母N表示
    

  • 每一个结点向下指向0或多个子节点，下图中N结点有两个子节点，用字母C表示
    

  • 每一个结点向上指向可能存在的唯一父节点，下图中N有一个父节点，用字母P表示
    

  • 如果一个结点不存在父节点，那么这是一个根节点，下图中Root是根节点
    

  • 如果一个结点不存在子结点，那么它是叶子结点，否则它是分支结点，下图中红框框是叶子，其他是分支
    

  • 一个结点的子节点数量称为度数
    

• 树

  • 树是多个结点的集合，结点的个数$n>=0$，下图中是多个结点的集合
    $Tre{e}_{Root}=[Root,N,B,C1,C2,C4,C5,g1,g2,g3,g4,g5,g6,g7,g8]$
    
  • 任何一个结点与它的所有子结点构成了另一颗完整的树，被称为子树，下图中$N$及其所有子节点构成了$Root$的左子树 $Tre{e}_N=[N,C1,C2,g1,g2,g3,g4]$，这也意味着$Tre{e}_{Root}\supset Tre{e}_N$（$Tre{e}_N$是$Tre{e}_{Root}$的子集)
    
  • 按照层次划分，一棵树从上至下层数逐一增加，值从0开始
    

平衡二叉树（AVL树）

平衡二叉树，又称AVL树，解决了二叉排序树高度不确定从而导致访问时间复杂度不稳定的情况，如果二叉排序树的子树间的高度相差太大，就会让二叉排序树操作的时间复杂度t提升，最坏的情况为O(n)，为了避免这种情况，平衡二叉树被发明，使树的任意结点左右子树高度差最小化，其本质还是一棵二叉搜索树。

• 定义（规则）

  • 每个结点最多有两个子结点（子树），如果都存在则分别为左子结点（子树）和右子结点（子树）

  • 除根节点外，每个结点必须区分左右

  • 对于任意节点N，N的左子树任意结点值 < N结点值 < N的右子树任意结点值，等值的结点必须划分到大于或小于分支中

  • 任意结点的左右子树高度差的绝对值<=1

  • 下图是一个正常的平衡二叉树
    

• 性质

  • 第 $i$ 层上最多有 $2^i$ 个结点
  • 一颗层数为 $l$ 的树最多有$2^{l+1}-1$个结点
  • 0度结