bfs 练习题

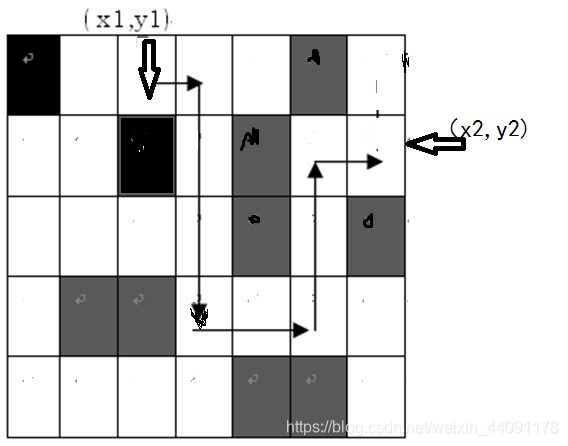
给出一张地图，这张地图被分为n×m（n,m<=100）个方块，任何一个方块不是平地就是高山。平地可以通过，高山则不能。现在你处在地图的（x1,y1）这块平地，问：你至少需要拐几个弯才能到达目的地（x2,y2）？你只能沿着水平和垂直方向的平地上行进，拐弯次数就等于行进方向的改变（从水平到垂直或从垂直到水平）的次数。例如：如图，最少的拐弯次数为5。

Input
第1行：n m
第2至n+1行：整个地图地形描述（0：空地；1：高山），
如（图）第2行地形描述为：1 0 0 0 0 1 0
第3行地形描述为：0 0 1 0 1 0 0
……
第n+2行：x1 y1 x2 y2 （分别为起点、终点坐标）
Output
s （即最少的拐弯次数）
Sample Input
5 7
1 0 0 0 0 1 0
0 0 1 0 1 0 0
0 0 0 0 1 0 1
0 1 1 0 0 0 0
0 0 0 0 1 1 0
1 3 1 7
Sample Output
5

#include<iostream>
#include<cstdio>
#include <queue>
using namespace std;
int n,m,x1,x2,y1,y2;
int a[101][101];
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
struct sa
{
    int x;
    int y;
    int xx;
    int yy;
    int bs;
};
void bfs(int x,int y)
{
    sa t,p;
    p.x=x;
    p.y=y;
    p.xx=x;
    p.yy=y;
    p.bs=0;
    queue<sa>q;
    q.push(p);
    while(!q.empty())
    {
        p=q.front();
        q.pop();
        if(p.x==x2&&p.y==y2)
        {
            printf("%d\n",p.bs);
            break;
        }
        for(int i=0;i<4;i++)
        {
            t.x=p.x+dx[i];
            t.y=p.y+dy[i];
            if(t.x>0&&t.x<=n&&t.y>0&&t.y<=m&&!a[t.x][t.y])
            {
                a[t.x][t.y]=1;
                if((t.x==p.x&&t.x==p.xx)||(t.y==p.y&&t.y==p.yy))/////拐弯的条件
                     t.bs=p.bs;
                 else
                     t.bs=p.bs+1;
                 t.xx=p.x;
                 t.yy=p.y;
                 q.push(t);
            }
        }

    }
}
int main()
{
      cin>>n>>m;
      for(int i=1;i<=n;i++)
          for(int j=1;j<=m;j++)
              cin>>a[i][j];
          cin>>x1>>y1>>x2>>y2;
          a[x1][y1]=1;
       bfs(x1,y1);

    return 0;
}