1、从前有座山,山里有座庙,庙里有个老和尚,再给小和尚讲故事,故事内容是:从前有座山,山里有座庙,庙里有个老和尚,再给小和尚讲故事,故事内容是:从前有座山,山里有座庙,庙里有个老和尚,再给小和尚讲故事,故事内容是……描述的是()
正确答案: E 你的答案: E (正确)
贪心回溯穷举分治递归
解题思路:
递归指的是一个过程:函数不断引用自身,直到引用的对象已知。
2、一个递归算法必须包括()
正确答案: B 你的答案: B (正确)
递归部分终止条件和递归部分迭代部分终止条件和迭代部分
解题思路:
递归就是指程序调用自身的编程思想,即一个函数调用本身;
迭代是利用已知的变量值,根据递推公式不断演进得到变量新值的编程思想。
递归体和递归出口
3、在递归算法执行过程中,计算机系统必定会用到的数据结构是( )
正确答案: C 你的答案: C (正确)
队列链表栈二叉树
解题思路:
栈的特点是“先进后处,后进先出”,在程序执行过程中,主程序先进栈,被调用的程序后进栈;当被调用程序结束后,先出栈,最后主程序运行结束了,主程序才出栈。 递归的过程,利用栈保存现场地址,然后将数据入栈,运算,后出栈,返回结果。
4、执行完下列语句段后,i值为()
| 1 2 3 4 5 |
|
正确答案: B
4488无限递归
解题思路:
f(x) 当x大于0时,返回x*f(x-1),否则返回2
f(0) = 2
f(1) = 1 * f(0) = 2
f(2) = 2 * f(1) = 4
f(3) = 3 * f(2) = 12
f(4) = 4 * f(3) = 48
f(4) = f(f(2)) = 48
5、只有那种使用了局部变量的递归过程在转换成非递归过程时才必须使用栈()
正确答案: B 你的答案: B (正确)
对错
解题思路:
递归工作栈里面包括返回地址、本层的局部变量和递归调用的形参代换用实参,所以正常情况下,无论递归过程有没有使用局部变量,转换为非递归过程都需要用栈来模拟这个递归调用过程
当然,有一些特殊递归不用栈就可以直接转换,比如尾递归、常系数递推等,无论是否有局部变量
6、以下关于递归调用的说法正确的是()
正确答案: C
函数间接调用自己不是递归递归调用可以用队列实现递归调用可以用栈实现函数直接调用自己是递归
解题思路:
递归的定义:
递归调用是一种特殊的嵌套调用,是某个函数调用自己或者是调用其他函数后再次调用自己的,只要函数之间互相调用能产生循环的则一定是递归调用。
递归的特点:
- 函数要直接或间接调用自身。 (A错误)
- 要有递归终止条件检查,即递归终止的条件被满足后,则不再调用自身函数,函数的调用原则和数据结构栈的实现是相一致。(类似于不断压栈,直到栈满,作为终止条件,C正确)
- 如果不满足递归终止的条件,则调用涉及递归调用的表达式。在调用函数自身时,有关终止条件的参数要发生变化,而且需向递归终止的方向变化。(函数直接调用自己加上递归的终止条件是递归,所以D错误)
7、设有一个递归函数如下
| 1 2 3 4 5 6 7 |
|
试问计算f(8)时,函数f返回( )。
正确答案: D
6789
解题思路:
考察的是递归运算原理。
8>3
所以f(8)=f(8-2)+f(8-4)+1
=f(6)+f(4)+1 6>3,4>3
=f(4)+f(2)+1+f(2)+f(0)+1+1
=f(2)+f(0)+1+f(2)+1+f(2)+f(0)+1+1
=1+1+1+1+1+1+1+1+1
=9
8、设有一个递归算法如下
| 1 2 3 4 |
|
试问计算f(f(9))时需要计算()次f函数。
正确答案: C 你的答案: C (正确)
10111214
解题思路:
一、先算内层f(9)
[1] 计算 f(9) = f(7) + f(3) + 1;
[2] 计算[1]中 f(7) = f(5) + f(1) + 1;
[3] 计算[2]中 f(5) = f(3) + f(-1) + 1;
[4] 计算[3]中 f(3) = 1;
[5] 计算[3]中 f(-1) = 1;
{至此f(5)可计算得: f(5) = 1 + 1 + 1 = 3}
[6] 计算(1)中f(1) = 1;
{至此f(7)可计算得 :f(7) = 3 + 1 + 1 = 5}
[7] 计算[1]中f(3) = 1;
{至此f(9)可计算得:f(9) = 5 + 1 + 1 = 7}
计算f(9)一共调用了7次函数
二、计算外层f(7)
由上面步骤可知,计算f(7)调用了5次函数
所以一共调用了函数7+5=12次
9、设有递归算法如下,最终打印结果是()
| 1 2 3 4 5 6 7 8 9 10 11 |
|
正确答案: A
3456
解题思路:
计算foo(1,3):此时a=1,b=3;
跳过两个if语句进入return foo(1+1,3/2)+1,即foo(2,1)+1;
计算foo(2,1):
同样,跳过两个if语句进入return foo(2+2,1/2)+2,即foo(4,0)+2;
计算foo(4,0):
进入第一个if语句,return 0;
逐层返回,得foo(2,1)=0+2=2;
再返回上一层,得foo(1,3)=2+1=3;
返回结果,foo(1,3)=3;
10、考虑下面递归表达式:

那么T(n)=()
正确答案: A 你的答案: A (正确)
O((LogLogn))^2
O((LognLogn))^2
O((LogLogn))
O((LognLogn))
解题思路:
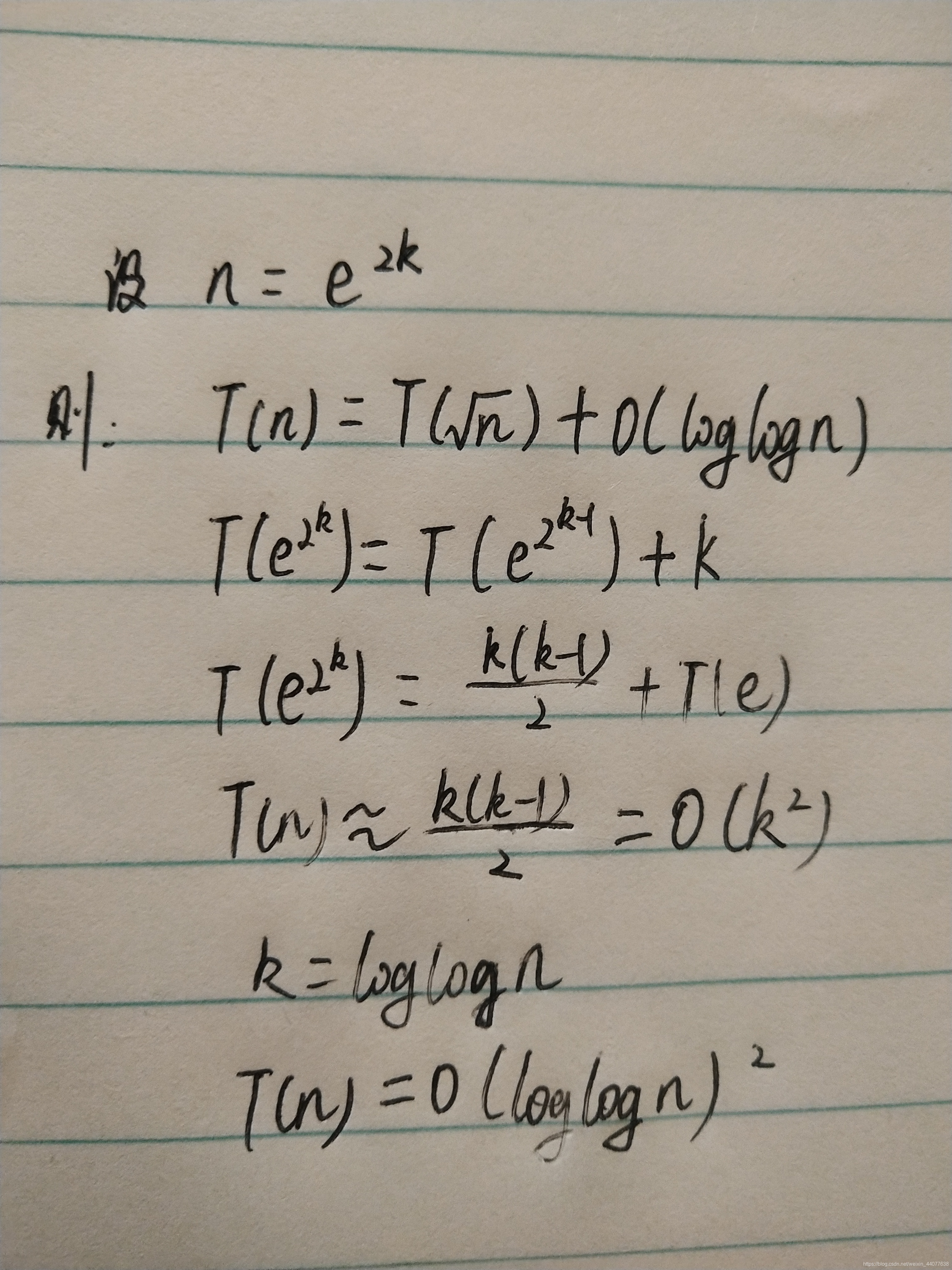








 本文详细介绍了递归的概念,特点以及在编程中的应用。通过解析递归问题的实例,如递归函数的调用过程,展示了递归在解决复杂问题时的思维方式。同时,文章还探讨了递归调用的栈数据结构,强调了递归终止条件的重要性,并通过一系列选择题帮助读者巩固理解递归的知识点。
本文详细介绍了递归的概念,特点以及在编程中的应用。通过解析递归问题的实例,如递归函数的调用过程,展示了递归在解决复杂问题时的思维方式。同时,文章还探讨了递归调用的栈数据结构,强调了递归终止条件的重要性,并通过一系列选择题帮助读者巩固理解递归的知识点。
















 1449
1449

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








