神经网络的权重初始化

神经网络的权重初始化方法对（weight initialization）对模型的收敛速度和性能有着至关重要的影响。因为，神经网络其实就是对权重参数w的不停迭代更新，以期达到较好的性能。在深度神经网络中，随着层数的增多，我们在梯度下降的过程中，极易出现梯度消失或者梯度爆炸。因此，对权重w的初始化则显得至关重要，一个好的权重初始化虽然不能完全解决梯度消失和梯度爆炸的问题，但是对于处理这两个问题是有很大的帮助的，并且十分有利于模型性能和收敛速度。一般来说，主要有四种权重初始化方法：

• 初始化为0
• 随机初始化
• Xavier initialization
• He initialization
  本文主要讨论后两种初始化方法。

Xavier initialization

Xavier initialization是 Glorot 等人为了解决随机初始化的问题提出来的另一种初始化方法，通过尽可能的让输入和输出服从相同的分布来避免后面层的激活函数的输出值趋向于0。初始化方法为：

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.

    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims)  # integer representing the number of layers
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(1 / layers_dims[l - 1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

Xavier initialization初始化后，每层激活函数输出值的分布如下图所示：

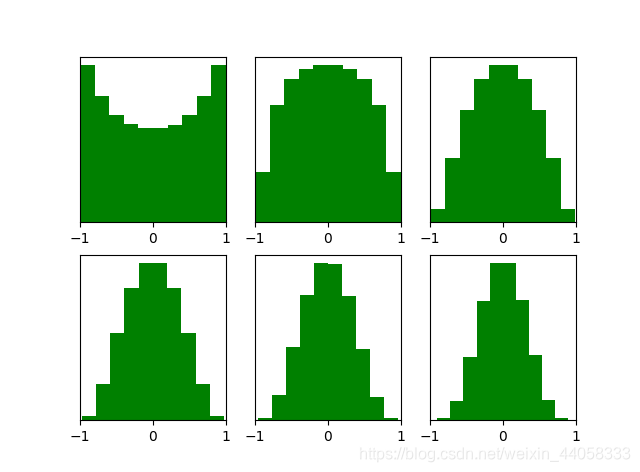
可以看出，激活函数输出值仍旧服从标准高斯分布。
这也说明Xavier initialization和tanH 激活函数是良好搭档，但对于目前神经网络中最常用的ReLU激活函数 却无能为力,当达到5，6层后几乎又开始趋向于0，更深层的话很明显又会趋向于0。

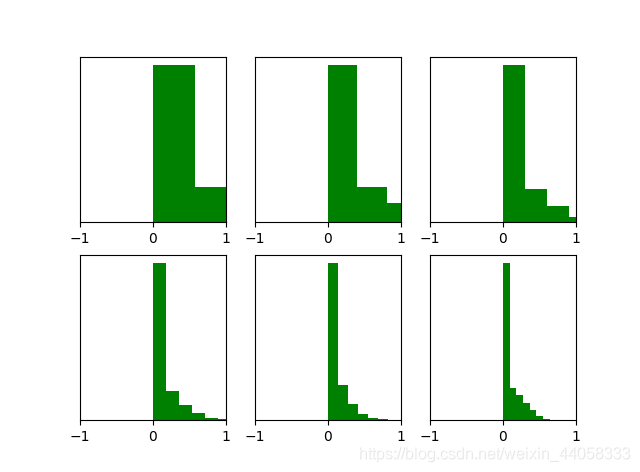
He initialization

为了解决上述问题，何恺明提出了一种针对ReLU的初始化方法，一般称作He initialization。初始化方式为：

def initialize_parameters_he(layers_dims):
    """
    Arguments:
    layer_dims -- python array (list) containing the size of each layer.

    Returns:
    parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":
                    W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])
                    b1 -- bias vector of shape (layers_dims[1], 1)
                    ...
                    WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])
                    bL -- bias vector of shape (layers_dims[L], 1)
    """
    np.random.seed(3)
    parameters = {}
    L = len(layers_dims)  # integer representing the number of layers
    for l in range(1, L):
        parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l - 1]) * np.sqrt(2 / layers_dims[l - 1])
        parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))
    return parameters

经过He initialization后，当隐藏层使用ReLU时，激活函数输出值的分布情况比Xavier initialization好很多。

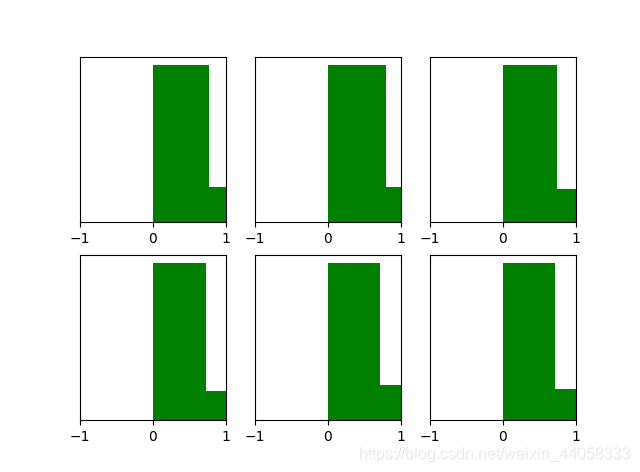
补充：

深度学习模型参数初始化都有哪些方法？

（1）Gaussian 满足mean=0，std=1的高斯分布x∼N(mean，std2)

（2）Xavier 满足x∼U(−a,+a)x∼U(−a,+a)的均匀分布， 其中 a = sqrt(3/n)

（3）MSRA 满足x∼N(0,σ2)x∼N(0,σ2)的高斯分布，其中σ = sqrt(2/n)

（4）Uniform 满足min=0,max=1的均匀分布。x∼U(min,max)x∼U(min,max)

等等
参考;
深度学习中神经网络的几种权重初始化方法