机器学习里的欧氏距离

最新推荐文章于 2025-01-05 12:37:05 发布

intelliphecy

最新推荐文章于 2025-01-05 12:37:05 发布

阅读量2.2k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：生物信息学文章标签：机器学习欧式距离

本文链接：https://blog.youkuaiyun.com/weixin_44054863/article/details/97319250

欧氏距离是机器学习中常用的计算两个观测间距离的函数，尤其在非监督学习如k-means聚类中，通过计算观测点与类别中心的距离来决定归属。在n维空间中，欧氏距离通过计算坐标差的平方和再开方得到。除了欧氏距离，R包philentropy提供了46种不同的距离算法供研究者使用。

“远在天边，近在眼前”，距离是一个需要定义的概念，对距离进行量化需要一个合适的坐标参考体系。在诗句里，距离可以很浪漫，“世界上最遥远的距离，不是生与死的距离，不是天各一方，而是，我就站在你的面前，你却不知道我爱你”。在机器学习里，距离是严谨的，需要一个精确的公式来计算。

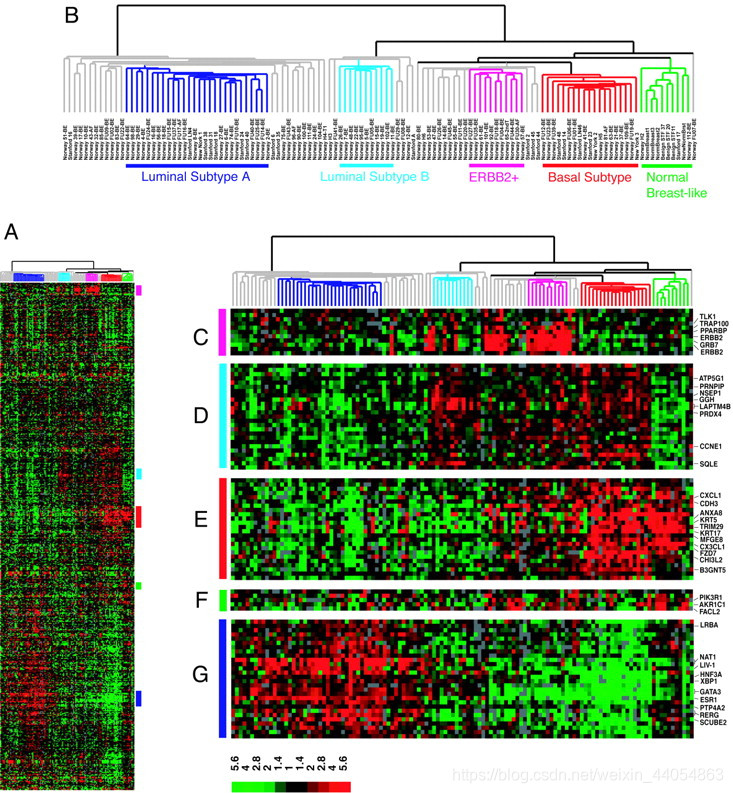
许多机器学习的常见算法都需要用到距离函数，即用于计算两个不同观测（obs）之间的距离。以癌症组织的转录组测序数据为例，不同的癌症样本即不同的观测，两个样本间的距离越短，意味着它们之间越相似，在各种非监督聚类算法中更容易被归为同一类。距离函数五花八门，欧氏距离应该算得上其中“最简单”和“最直观”的距离函数了。

在数学上，欧氏距离是欧氏空间里两点间的直线距离。在一个二维空间里，两个点p1和p2的坐标分别为(x1, y1), (x2, y2)。那么p1和p2的距离d(p1, p2)等于sqrt((x1-x2)2+(y1-y2)2)。同理，在一个三维空间里，两个点p1和p2的坐标分别为(x1, y1), (x2, y2) , (z2, z2)。那么p1和p2的距离d(p1, p2)等于sqrt((x1-x2)2+(y1-y2)2+(z1-z2)2)。简单的说，在二维和三维空间里，两个点间的距离就是它们在欧氏空间里的真实距离。事实上，两个数据点的情形就是毕达哥拉斯定理用两个直角边计算斜边的公式。

现实中，我们的数据维度往往高于三维。对于n维空间里的两个点p1和