《并行计算》稠密矩阵运算

矩阵的划分

带状划分

矩阵划分可以按照行划分，也可以按照列划分；进一步的，上面这两种划分又有两种方式，一种是块带状划分，一种是循环带状划分

棋盘划分

块棋盘划分和循环棋盘划分的一个例子如下
可以看到，块棋盘划分其实蛮好理解的，就是将二维数组分成一个一个的小格，而循环棋盘划分就是将不同区域的元素选择性聚合在一起，形成小格。

矩阵转置

棋盘划分的矩阵转置

网孔上的矩阵转置

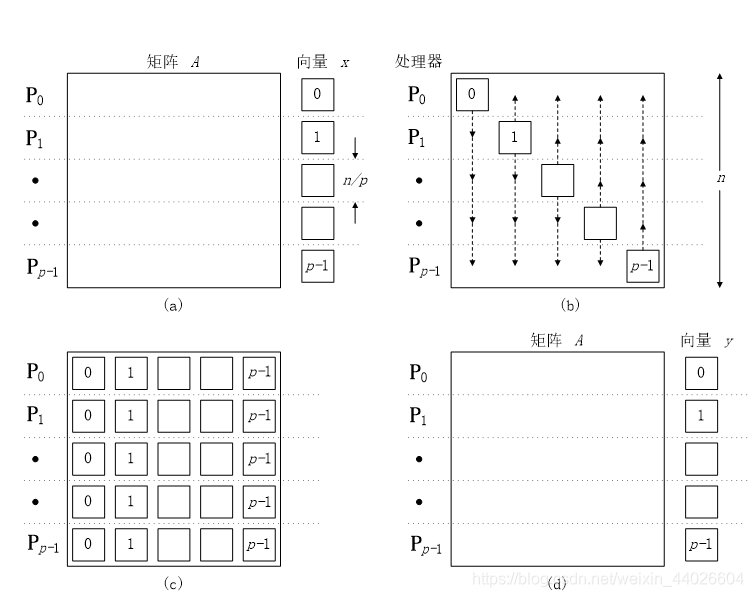
p = n²的情形

通信过程像（a）中的虚线所描述，转置结果如图（b）

p < n²的情形

将矩阵划分成p个大小的子块，
运行时间：

子块转置后子块内局部转置（注意这里是局部哈，不看仔细的话，容易认成是两次转置）

超立方上的矩阵转置

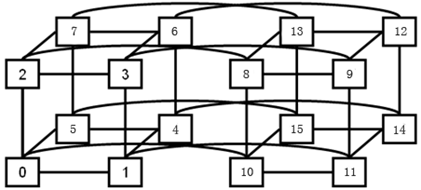
基本思路还是要把超立方转换成网孔来解决，如下图：

运行时间：

带状划分的矩阵转置

将A_n×n分成 p 个【(n/p)×n】大小的带，P_i有(p-1)个（对角线上的不用算）(n/p)×(n/p)大小的子块发送到另外的(p-1)个处理器中，每个处理器本地交换相应的元素。

矩阵-向量乘法

带状划分的矩阵-向量乘法

行带状划分

按照一般的任务分配方式，P_i存放x_i和矩阵的行块，并输出y_i

p=n时，每个P_i向其他处理器播送x_i（多到多播送），每个处理器就可以单独根据所分配的矩阵行块和收集到的向量，进行独立的计算，最后将结果汇总就好

p<n时，其实道理一样，只不过是将若干行划分在一起。

超立方连接的计算时间：

网孔连接的计算时间：

棋盘划分的矩阵-向量乘法

棋盘划分比带状划分快

矩阵乘法

简单并行分块乘法

首先简单地将A，B矩阵等划分为规模为
的方块阵，存放在相应的处理器当中。

算法分为两部分，一部分是通信方法，将每行处理器进行A矩阵块的多到多播送，每列处理器进行B矩阵块的多到多播送；一部分是计算方法，每个处理器计算：

运行时间：

• 超立方：
  
• 二维环绕网孔：
  
  对该算法的评价：
• 每个处理器都需要存储2√p 个块，对处理器的存储要求过大

Cannon乘法

Cannon乘法就是用来解决简单并行分块乘法对存储器存储要求高的缺点而提出的，分块还是按照一般的棋盘分块来做。下面是其计算C₀₀的一个例子，从中可以窥探出Cannon乘法的基本方法论：

算法机制：

C₀₀的计算，看似还好，但其实Connon算法对初始矩阵的排列是有要求的：

按照上面的方法初始化矩阵之后，以后就只管将A的每个块向左循环移动一步，将B的每个块向上循环移动一步：


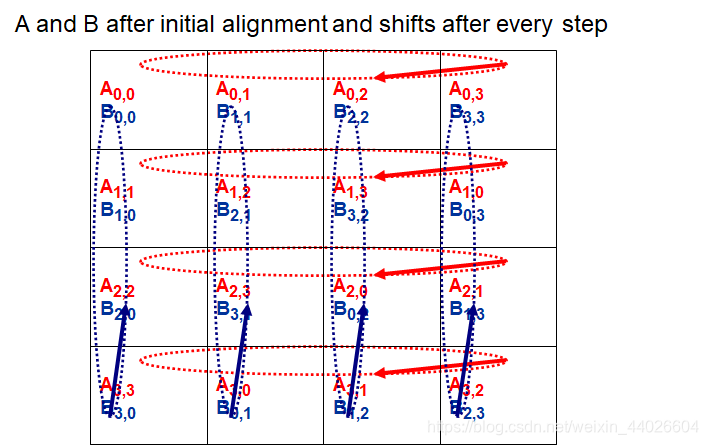
算法分析：

Fox乘法

还是进行一样的分块，

DNS乘法

处理器数为n³，运行时间O(logn)，速度非常快


4*4矩阵在64个处理器上的DNS乘法：