算法分析与设计-作业二-Dijkstra算法

最新推荐文章于 2021-06-04 13:33:43 发布

原创最新推荐文章于 2021-06-04 13:33:43 发布 · 269 阅读

0 ·

CC 4.0 BY-SA版权

本文深入解析了Dijkstra算法，一种用于解决单源最短路径问题的经典算法。文章详细阐述了算法的设计思路，包括如何利用Collected数组判断顶点是否被收录，如何使用dist数组保存最短路径，以及path数组保存上一个连接的顶点。通过逐步分析，读者可以理解Dijkstra算法的具体实现过程，包括初始化、收录原点、更新最短路径等关键步骤。

Dijkstra算法：单源最短路径

1、问题：

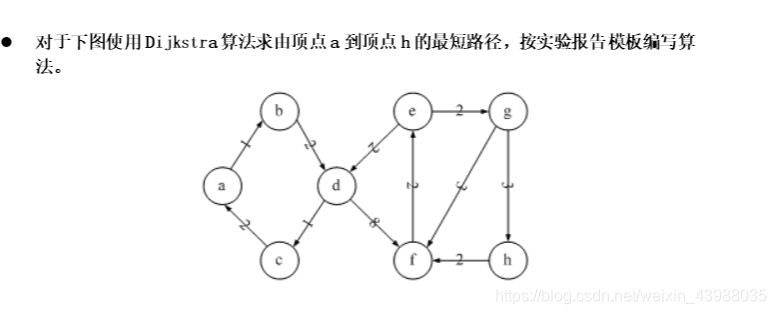
在这里插入图片描述

2、算法分析：

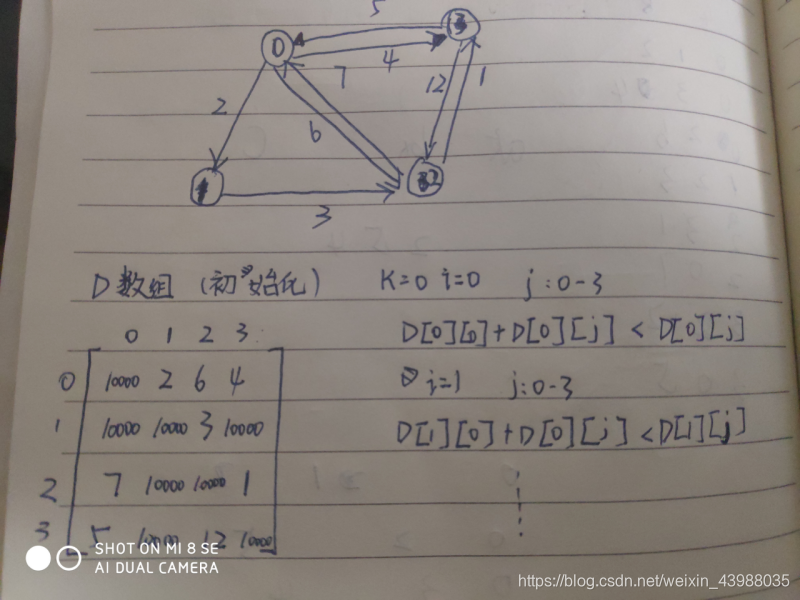
在这里插入图片描述

3、算法设计

Collected数组用来判断顶点是否被收录，dist用来保存最短路径，path保存上一个连接的顶点
s为原点
先初始化数组：
Collected=0
Dist[v]=Graph->G[s][v];v:0->Graph->nv-1
Path[v]=s;
/*/收录s原点：
Dist[s]=0;
Collected[s]=1;
Path[s]=-1;
While(1){
V=/未收录顶点中最小权值的点/
如果v==-1 break;
/更新dist/
如果w未收录且与v连通
如果Graph->G[v][w]<0return flase
如果Dist[v]+Graph->G[v][w]<dist[w]
更新dist[w]
}
Return true
}