Knowledge Graph Embeddings
- 一、 Heterogeneous Graphs and Relational GCN (RGCN)
- 二、 Knowledge Graphs: KG Completion with Embeddings
- 三、 Knowledge Graph Completion: TransE, TransR, DistMult, ComplEx
一、 Heterogeneous Graphs and Relational GCN (RGCN)
之前讲的都是同质图的嵌入。这里讲有多种边类型图,即异质图的嵌入。
异质图包括三种:

1.Heterogeneous Graphs and Relational GCN (RGCN)
异质图的定义:
即,是由四元组定义的。其中每个节点有其对应的类型
T
T
T,每个边也有对应的类型
R
R
R。

异质图的例子:

2.Relational GCN
现在想把GCN扩展到异质图上。这是最简单的一种异质图,只有一种连边,有多种节点类型。目标是学习节点A的表示:

这种图中,消息传递只发生于一部分节点之间。
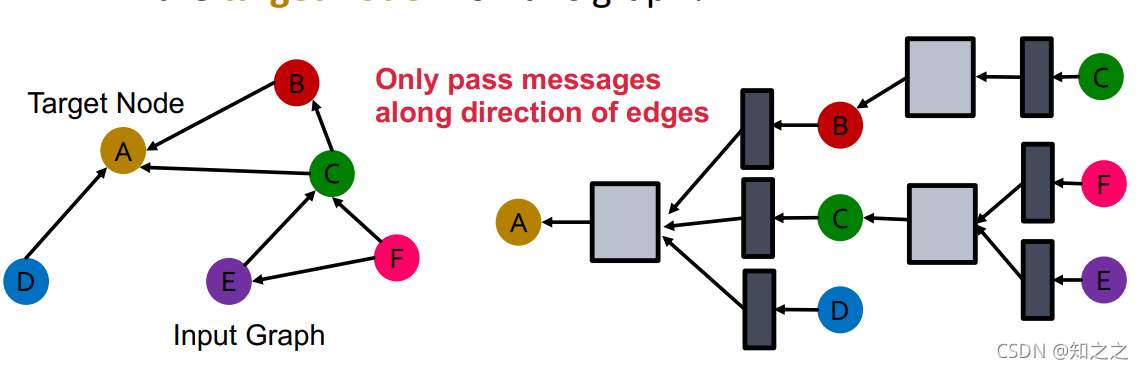
回忆一下GCN的组成部分:

一个典型的GCN结构是,消息处理函数为带 权值的线性投影;聚合函数为求和函数:
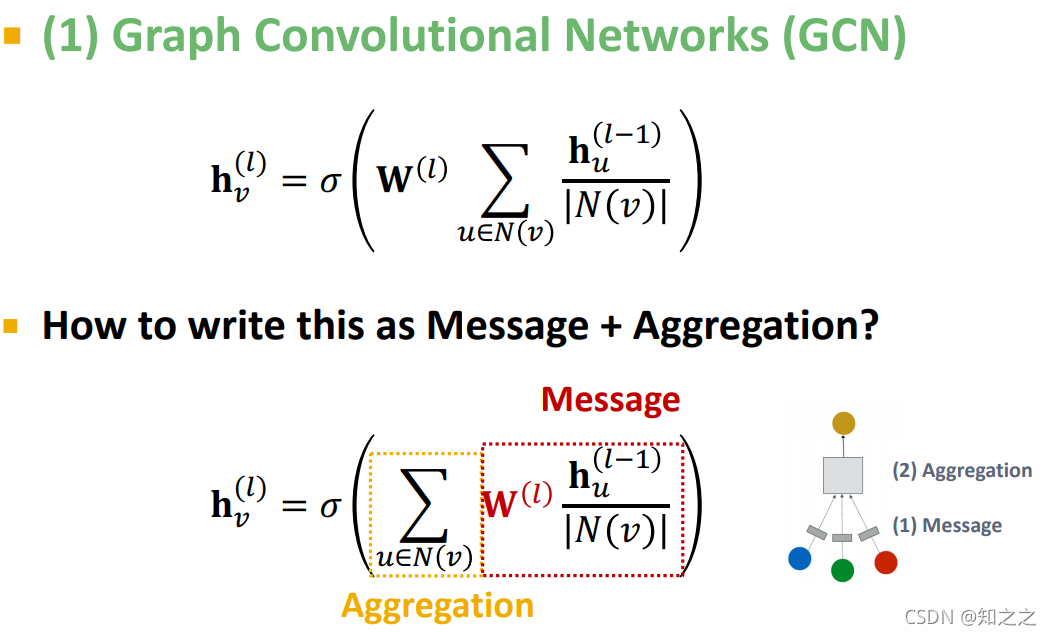
但是如果是多重边的集合呢?怎么变化一下呢?这里采用的是,对不同类型的边,使用不同的投影矩阵。上面的公式中,对所有边,都是使用同一个投影矩阵(在每一层都有一个矩阵)。在异质图中,可以给每种类型的边设计一个独立的矩阵:

这样一来,GCN的消息传递模型就可以画成下图,其中每一种颜色代表了一种边类型,也对应着一个独立的权值矩阵W:

这样就可以定义传播函数了。下式中,每个W都对应一种边类型的投影矩阵。

那么如何将这个函数写成标准的GNN模板呢?如下图,对消息的处理有两部分,前面的矩阵是处理邻居节点,其中每个矩阵对应一种类型;后面的消息处理自环,是自己的投影矩阵。然后聚合函数就是求和。

但是这么定义的模型,参数量是个大问题。因为每一层,每一种类型的边,都对应一个投影矩阵。当边类型太多时,这参数量太大了,且这些矩阵通常是密集的:

这样的参数量,会导致过拟合。有两种方法解决这个问题:

(1) block diagonal matrices
即,让权重参数变得稀疏:

但这方法有个问题, 即只有附近的节点才能传递信息:

这样的矩阵的确是减少了参数量:

(2)basis learning
即,在不同的嵌入矩阵之间共享参数。下图中,V是基础矩阵,a是权重参数。这样一来,模型只学习权重参数a即可。这种方法也叫“dictionary learning”

3.RGCN链路预测应用
节点分类很简单,就是用最后一层的输出做分类。这里就不提了。
(1)验证集、训练集的划分
链路预测复杂一些,需要将不同类型的边逐一分成四个集合,然后合并起来做训练、测试啥的。
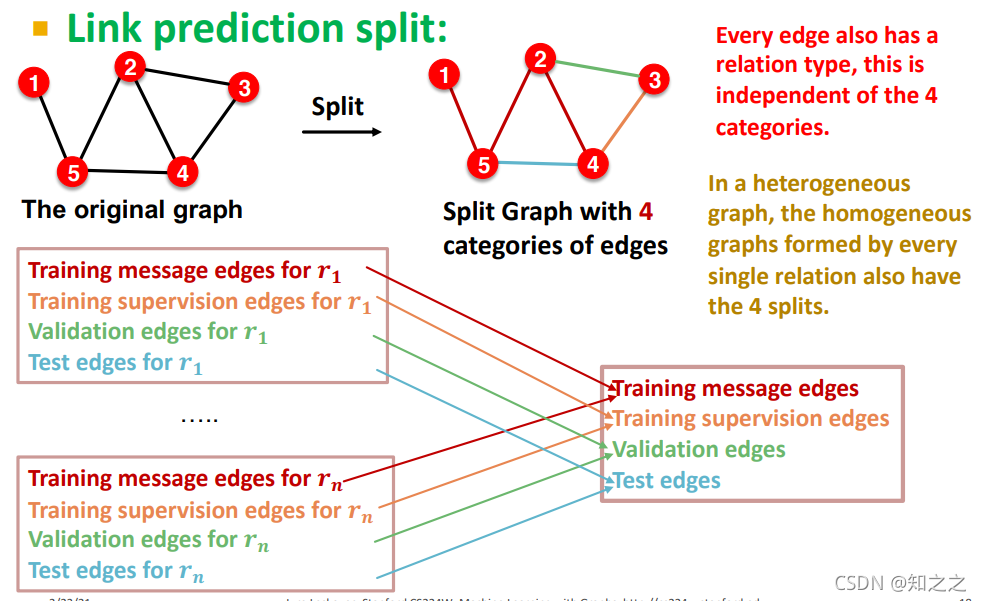
例子:

(2)边的得分函数
如果在上图中,想要给
(
E
,
r
3
,
A
)
(E,r_{3},A)
(E,r3,A)边打分,那么需要将这个边当做训练边,其他边当做消息传递边。然后用E和A的最后一层的输出作为参数,得出
(
E
,
r
3
,
A
)
(E,r_{3},A)
(E,r3,A)的得分:

(3)负采样的方法
训练的具体过程如下,即先根据训练边
(
E
,
r
3
,
A
)
(E,r_{3},A)
(E,r3,A)做负采样(即采样不存在的边),然后训练。注意这里的负采样的边,不能是消息传递的边。

(4)训练流程
具体流程:

(5)验证、测试阶段
验证:

测试:

二、 Knowledge Graphs: KG Completion with Embeddings
1.什么是KG
一个例子:其中有实体、有关系。且这两者都有不同的类型:

KG就是一种异质图:

2.KG的应用
现实中,有很多应用:

如Serving information 应用:

Question answering and conversation agents:

3.KG的数据集


三、 Knowledge Graph Completion: TransE, TransR, DistMult, ComplEx
1.知识图谱补全任务描述 KG Completion Task
问题描述:给定实体的头和关系,预测尾结点。For a given (head, relation), we predict missing tails.这和链路预测是有些不同的。
下图中,任务是根据JKRowling这个实体和genre这个边,预测其尾结点Science Fiction:

2.KG的表示
一种简单的方法就是前面的查找表:

每个实体、关系都用一个向量表示:

关键思想:在向量空间
R
d
\mathbb{R}^{d}
Rd中建模真正的关系:

那么问题来了,如何嵌入?如何定义相近的概念?
4.KG中关系的模式 Connectivity Patterns in KG
首先定义一下关系模式。
一个图中,关系有多种属性(如对称关系)。那么TransE能捕获到这些关系吗?
首先列举了几种不同的关系:
分别是
- 对称关系(如舍友关系)
- 反演关系(如导师、学生关系)
- 组合关系(如母亲的丈夫,是父亲)
- 1对N关系(如 是…的学生)

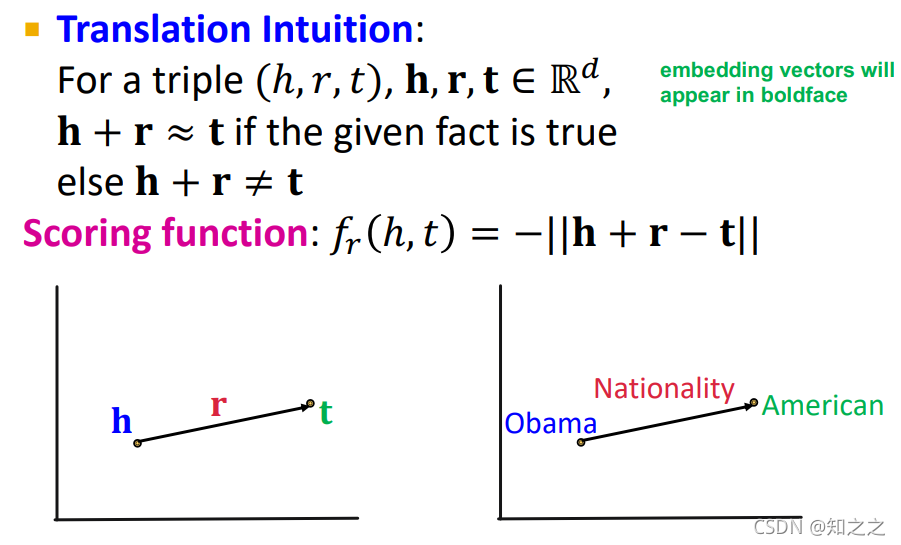
4.TransE
最简单的翻译模型。想让奥巴马+国籍=美国。有点像一阶谓词。
 算法伪代码如下。
算法伪代码如下。
首先随机初始化三种表示,然后负采样(即采样那些图中不存在的三元组,比如奥巴马+国籍=日本),然后是对比损失函数:

(1)Antisymmetric Relations
TransE中,能捕获反对称关系:

(2)Inverse Relations
这个也是可以的

(3)Composition (Transitive) Relations
可以。

(4)Limitation:Symmetric Relations
这个关系是捕获不了的。如舍友关系。这要求
∥
h
+
r
−
t
∥
=
∥
t
+
r
−
h
∥
=
0
\left \| h+r-t \right \| = \left \| t+r-h \right \| = 0
∥h+r−t∥=∥t+r−h∥=0。但是由于
h
和
t
h 和 t
h和t是不同的实体,因此它们位于嵌入空间中不同的位置,因此不能满足:

(5)Limitation: 1-to-N relations
StudentsOf这个关系也满足不了:

5.TransR
(1)TransR的思想
TransE将所有关系、实体,都建模在同一个空间中。那么能否在relation-specific space的空间中(即给关系分配不同的向量空间)建模关系呢?
TransR的思想就是:实体在实体的空间中,关系在关系的空间中。通过一个个投影矩阵,将实体投影到关系空间:
注意是给每种
关系分配一个投影矩阵
M
r
M_{r}
Mr。


(2)Symmetric Relations
对于对称关系,就可以将$
h
和
t
h 和t
h和t投影到同一个位置,此时满足对称关系:

(3)Antisymmetric Relations

(4)1-to-N Relations

(5)Antisymmetric Relations

(6)Limitation:Composition Relations

6.New Idea: Bilinear Modeling(DistMult)
(1)DistMult
模型叫DistMult,使用了Bilinear Modeling的思想
这玩意叫“双线性模型”。
思想是,把实体、边当做向量:

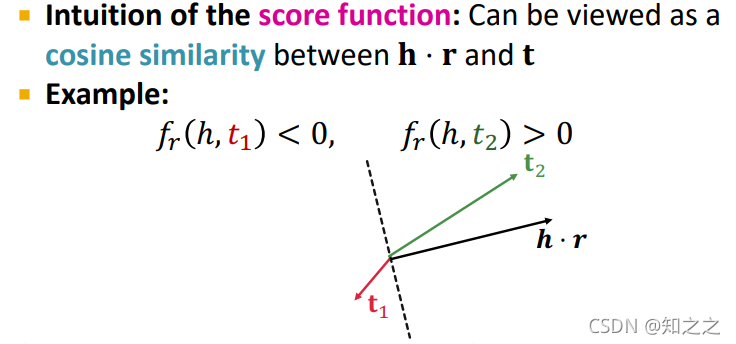
用点积作为得分函数:

这背后的直觉是,点积即
h
,
r
,
t
h,r,t
h,r,t之间的余弦相似度:
后面也分析了这个模型的表示力,不想看了。跳过。
7.ComplEx
基于Distmult,ComplEx在复数域建模实体、关系的特征:


后面也是分析了这方法的表示力(即能否表示出上述各种属性的关系)。跳过。
8.各种模型表示力的总结

9.应用建议
- 不同的KG可能有全然不同类型的边
- 没有十全十美的方法。可以根据上面的表,选择适合自己的
- 如果没有太多的对称关系,可以先用TransE试试
- 然后用复杂的模型

9.本节总结
链路预测、补全KG是主要的KG任务。
介绍了集中补全方法。




























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








