斯特林数（Educational Codeforces Round 86 (Rated for Div. 2) E. Placing Rooks）

最新推荐文章于 2022-04-10 14:27:21 发布

原创最新推荐文章于 2022-04-10 14:27:21 发布 · 254 阅读

1 ·

CC 4.0 BY-SA版权

M 专栏收录该内容

32 篇文章

订阅专栏

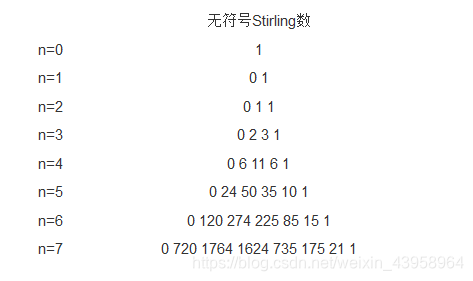
第一类斯特林数：
将n个不同元素分为m个环(圆排列)的方案数。（细分还有带符号和不带符号的第一类斯特林数）
推导： dp(m,n)表示n个不同元素组成m个环的方案数，这边求方案数，有点计数dp的味道，事实也是，最后一个元素可以分两个状态，一个自己成环，另一个加入别人，如果n个元素构成了m-1个圆排列，第n+1个元素独自构成一个圆排列；如果n个元素构成了m个圆排列，将第n+1个元素插入到任意元素的左边；n个元素构成的x圆排列，x小于m-1时就根本构成不了m个圆排列，总方案数：，dp(m,n+1)=dp(m-1,n)+dp(m,n)*(n)。
在这里插入图片描述

$\sum_{k=0}^ns(n,k)$ =n! (s(n,k)表示n个不同元素k个圆排列)
注意s(0,0)=1。

第二类斯特林数：
将n个不同的元素分为m个非空集合的方案数。
推导： 和第一类Stirling数不同的是，集合内是不考虑次序的，而圆排列是有序的。常常用于解决组合数学中几类放球模型。描述为：将n个不同的球放入m个无差别的盒子中，要求盒子非空，有几种方案？
推导的切入点和第一类基本一致。
如果n个元素构成了m-1个集合，那么第n+1个元素单独构成一个集合。
如果n个元素已经构成了m个集合，将第n+1个元素插入到任意一个集合
dp(m,n+1)=dp(m-1,n)+dp(m,n)*(m)。
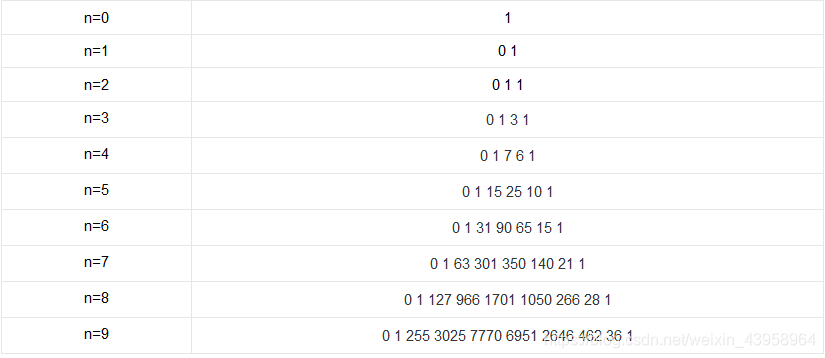
在这里插入图片描述

$\sum_{k=0}^nS(n,k)$ = $B_n$ ， $B_n$ 是贝尔数。(S(n,k)表示n个不同元素拆分为k个集合的方案数)

第二类斯特林数的通项公式： S(n,m)= $\frac{1}{m!}$ $\sum_{k=0}^mC_m^k(-1)^k(m-k)^n$
这里多说一句组合的恒等式C(n,m)=C(n-1,m-1)+C(n-1,m)，定义推理就能得证。
推导：
这边为了区分集合，先标号，最后除以 $m!$ 即可。
从空盒子入手，先不考虑空盒子一共有 $m^n$ 的方案数，其中包含了空盒子的方案数，设空盒子数量是h时的方案数是T(h)种，即 $m! * S (n, m) = T (0)$ ， $m^n=\sum_{h=0}^mT(h)$ 。
需要解决空盒数大于0的情况。先选定一个空盒子剩余的随便放置，则： $C_m^1*(m-1)^n$ 。那么空盒数为h的情况被计算了几次？由于空盒必须要有一个出现在被选定的位置，重复次数是 $C_h^1$ 。之后看一般的情况，计算空盒数不小于k的情况有 $C_m^k*(m-k)^n$ ,可得 $C_m^k*(m-k)^n=\sum_{h=0}^mC_h^kT(h)$ 。
继续为了消除系数 $\sum_{k=0}^h(-1)^kC_h^k=(1-1)^h=0^h$ ;那么继续 $\sum_{k=0}^m(-1)^kC_m^k(m-k)^n=\sum_{k=0}^m(-1)^k\sum_{h=0}^mC_h^kT(h)=\sum_{h=0}^mT(h)\sum_{k=0}^m(-1)^kC_h^k=\sum_{h=0}^mT(h)0^h=T(0)=m!S(n,m)$
解得
S(n,m)= $\frac{1}{m!}\sum_{k=0}^mC_m^k(-1)^k(m-k)^n$

这是一种证明方法，但我个人更倾向公式法的推理证明，过程实在不好打(可能是懒)，我写在草稿本上了，可能比较丑，但条理还是比较清晰的。有错误的地方还请提醒一下。

在这里插入图片描述

最后带一条两类Stirling数之间得关系：
$\sum_{k=0}^nS(n,k)s(k,m)=\sum_{k=0}^ns(n,k)S(k,m)$
类似于矩阵的对称转置关系。

附上一道例题其他例题待更。
题目：Educational Codeforces Round 86 (Rated for Div. 2) E. Placing Rooks
题意：在一个n*n的棋盘里，放n个车，确保n * n的棋盘里每一个格点都能被车攻击，并且保证k对车能相互攻击(中间没有其他车就是一对可攻击的在同一行或者同一列)，车就是象棋里的车能走完一列或者一行，求总的情况数。

先考虑按行放n个就必然全部能攻击到，列本质和行相同乘以2就行。
以按行放的情况我们现在只考虑列方向就可以了。如果要求k的话，存先考虑最大有车的列数，k+1个车在同一列，这样必成立，其余n-(k+1)在其他列，那么会发现一共是n-k列，基于这种情况无论怎么移动车到另一列都是成立的一方+1一方减1，总和k未变，一旦超出n-k，那么无法达到k个相对。
这样就可直接推导了， $C_n^{n-k}*S(n,n-k)*(n-k)!$ ，S(n,n-k)就是第二类斯特林数。k=0时，显然是n!。

#include<cmath>
#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cstdlib>
#include<istream>
#include<vector>
#include<stack>
#include<set>
#include<map>
#include<algorithm>
#include<queue>
#define inf 0x3f3f3f3f
#define llinf 0x3f3f3f3f3f3f3f3f
#define MAX_len 50100*4
using namespace std;
typedef long long ll;
const int mod=998244353;
ll num[200100];
ll quickpow(ll a,ll n)
{
    ll res=1;
    while(n)
    {
        if(n&1)
        {
            res=(res*a)%mod;
        }
        a=(a*a)%mod;
        n>>=1;
    }
    return res;
}
ll C(ll x,ll n)
{
    ll temp=num[n]*(quickpow((num[n-x]*num[x])%mod,mod-2));
    temp%=mod;
    return temp;
}
int main()
{
    ll n,k,i,j;
    scanf("%I64d %I64d",&n,&k);
    num[1]=1;
    num[0]=1;
    for(i=2;i<=n;i++)
    {
        num[i]=(num[i-1]*i)%mod;
    }
    if(k>=n)
    {
        printf("0");
        return 0;
    }
    if(k==0)
    {
        printf("%I64d",num[n]);
        return 0;
    }
    ll ans=0;
    for(i=0;i<n-k;i++)
    {
        ans=(ans+(quickpow(n-k-i,n)%mod)*(C(i,n-k)%mod)*(quickpow(-1,i))+mod)%mod;
    }
    ans=ans*C(n-k,n);
    ans%=mod;
    ans=(ans*2)%mod;
    printf("%I64d",ans);
    return 0;
}