CCF CSP认证201312-4 有趣的数（排列组合计算||DP动态规划）

201312-4 有趣的数（排列组合计算||DP动态规划）

题目

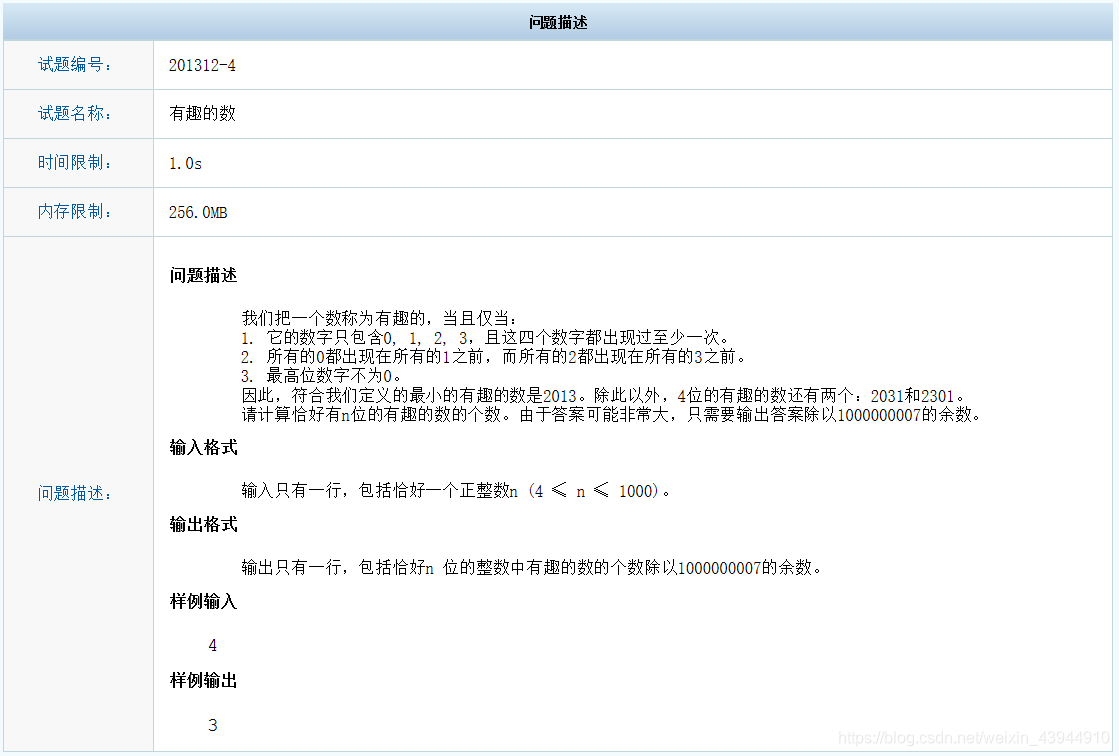
思路

- 看到大佬们的DP，都不好意思贴自己的渣渣代码了
硬生生当一个数学题做，O(n ² )的时间空间复杂度

• 由于n<=1000，组合数可以直接先递推算出来。
• 开头必须是2。因此不考虑开头的2，总个数为n-1，2的个数可为0。
• 可以把数分成两部分，0、1和2、3。对于特定的n23及n01，0、1个数情况有（n01-1）种，2、3个数情况有n23种。（0的个数取值范围为1至n01-1，2的个数 取值范围为0至n23-1。）

AC代码如下

#include<cstdio>
const int M=1e9+7;
long long c[1001][1001]={0};//保存组合数，long long防溢出

int main(){
    int n;
    long long ans=0;
    scanf("%d",&n);
    for(int i=0;i<=n;i++) c[0][i]=c[i][i]=1;
    for(int i=2;i<=n;i++){//递推求组合数
        for(int j=1;j<=i/2;j++){
            c[j][i]=(c[j][i-1]+c[j-1][i-1])%M;
            c[i-j][i]=c[j][i];
        }
    }
    n--;//除去开头的2
    for(int n23=1;n23<=n-2;n23++){//n23表示2、3总个数除去开头的2
        bool flag=0;
        if(n23>n/2) {flag=1;n23=n-n23;}//当n23比n01大的时候反一下
        int n01=n-n23;
        long long t=0;//t记录将0、1与2、3混合在一起的情况数
        for(int i=0;i<n23;i++){
            //将2、3序列切割i刀，在0、1序列n01+1条缝中选i+1个，填入
            t=(t+c[i][n23-1]*c[i+1][n01+1])%M;
        }
        if(flag) {n01=n23;n23=n-n23;}//把n01与n23换回来，以便下次循环
        ans=(ans+t*(n01-1)*n23)%M;
    }
    printf("%lld\n",ans);
    return 0;
}

(2019.9.9)
dp做法，O(n)

递推过程：
由题目条件可知

• 长度为n的0,1,2,3序列，可由长度为n-1的
  $$0,1,2,3序列末尾补1或3$$$$2,0,1序列末尾补3$$$$2,0,3序列末尾补1$$得来。易知这三种情况的序列是不会重复的，且不会出现0在1后、2在3后的情况。
• 长度为n的0,2,3序列，可由长度为n-1的$$0,2,3序列末尾补0或3$$$$0,2序列末尾补3$$$$2,3序列末尾补0$$得来。易知这三种情况的序列是不会重复的，且不会出现2在3后的情况。
• 长度为n的0,2,1序列，可由长度为n-1的$$0,2,1序列末尾补1或2$$$$0,2序列末尾补1$$得来。易知这两种情况的序列是不会重复的、且不会出现0在1后的情况。
• 长度为n的2,3序列，可由长度为n-1的$$2,3序列末尾补3$$$$2序列末尾补3$$得来。易知这两种情况的序列是不会重复的、且不会出现2在3后的情况。
• 长度为n的0,2序列，可由长度为n-1的$$0,2序列末尾补0或2$$$$2序列末尾补0$$得来。易知这两种情况的序列是不会重复的。
• 长度为n的2序列，情况只有一种。

由于所有的序列最初都由2序列末尾补数字而来，故可保证0,1,2,3序列开头为2。

AC代码如下

#include<cstdio>
const int M=1e9+7;
long long f[2][6]={0};//滚动数组降维（实测在这里屁用没有）
int main(){
    	int n;
    	scanf("%d",&n);
    	for(int i=1;i<=n;i++){
     		int k=i&1;
     		f[k][0]=1;//2序列 
     		//2,0 原序列尾巴加0或2、或2序列尾巴加0 
     		f[k][1]=(f[!k][1]*2+f[!k][0])%M;
     		//2,3 原序列尾巴加3、或2序列尾巴加3
     		f[k][2]=(f[!k][2]+f[!k][0])%M; 
     		//0,2,1 原序列尾巴加1或2、或02序列尾巴加1
     		f[k][3]=(f[!k][3]*2+f[!k][1])%M; 
     		//0,2,3 原序列尾巴上加0或3、或02序列尾巴加3、或23序列尾巴加0
     		f[k][4]=(f[!k][4]*2+f[!k][1]+f[!k][2])%M;
     		//0,1,2,3 原序列尾巴加1或3、或021序列尾巴加3、或023序列尾巴加1 
     		f[k][5]=(f[!k][5]*2+f[!k][3]+f[!k][4])%M;
 	}
 	printf("%lld",f[n&1][5]);
    	return 0;
}

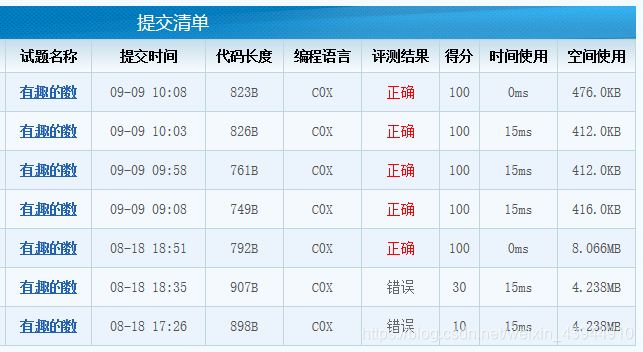
想不通这样的程序居然要花费416kB的内存，不用滚动数组476
猜测是乘法和取模花了太多空间，于是进行了我认为的优化，才省了4K…

#include<cstdio>
const int M=1e9+7;
long long f[2][6]={0};
long long Mod(long long x){//底层的取模运算或许就是这么实现的，这个函数半点优化效果都没有
 	while(x>=M) x-=M;
 	return x;
}
int main(){
    	int n;
    	scanf("%d",&n);
    	for(int i=1;i<=n;i++){
     		int k=i&1;
     		f[k][0]=1;
     		f[k][1]=Mod((f[!k][1]<<1)+f[!k][0]);//把乘2换成右移，省了4KB
     		f[k][2]=Mod(f[!k][2]+f[!k][0]);  
     		f[k][3]=Mod((f[!k][3]<<1)+f[!k][1]);
     		f[k][4]=Mod((f[!k][4]<<1)+f[!k][1]+f[!k][2]);
     		f[k][5]=Mod((f[!k][5]<<1)+f[!k][3]+f[!k][4]);
 	}
 	printf("%lld",f[n&1][5]);
    	return 0;
}

好吧我知道了，这是csp评测机的问题，412.0KB已经是我提交的所有题目的最小值了…
这几天洛谷刷多了==