矩阵旋转变换,就是说给定一个角度和点,我们将点绕着一个坐标轴旋转。在旋转过程中发生变化的总是x,y,z三个坐标里面的其中两个,而不让第三个坐标值变化。这意味着,旋转路径总在三个坐标轴平面中的一个之中:绕 Z 轴的是 XY 面、绕 X 轴的是 YZ 面、绕 Y 轴的是 XZ 面。还有许多复杂的旋转变换可以让你绕任意一个向量旋转,但是眼下我们并不需要讨论这些。
让我们概括地定义这个问题这个问题,看看下面的这个图:
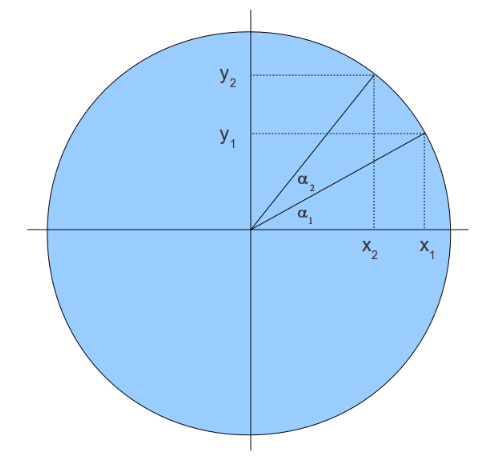
我们想沿着圆圈从(x1,y1)移动到(x2,y2)。也就是说我们让向量(x1,y1)转过 a2 角度。我们假设这个圆的半径是 1。这意味着下列成立:
x1 = cos(a1)
y1 = sin(a1)
x2 = cos(a1+a2)
y2 = sin(a1+a2)我们用下面的三角恒等式来产生 x2 和 y2 :
cos(a+b) = cos(a)*cos(b) - sin(a)*sin(b)
sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b)通过面的式子我们可以推导出:
x2 = cos(a1+a2) = cos(a1)*cos(a2) - sin(a1)*sin(a2) = x1*cos(a2) - y1*sin(a2)
y2 = sin(a1+a2) = sin(a1)*cos(a2) + cos(a1)*sin(a2) = y1*cos(a2) + x1*sin(a2)在上面的图中我们看向 xy 平面,Z 轴指向屏幕内部!如果 X 分量和 Y 分量是四维向量的一部分,那样上面的等式可以写成下面的矩阵形式(不影响 Z 和 W )为:

如果我们想创建一个绕着 X 轴或者绕着 Y 轴的旋转变换矩阵,那么方程基本相同但是矩阵的安排却略有不同!这是绕 X 轴旋转的矩阵:
y1 = cos(a1)
z1 = sin(a1)
y2 = cos(a1+a2)
z2 = sin(a1+a2)
y2 = cos(a1+a2) = cos(a1)*cos(a2) - sin(a1)*sin(a2) = y1*cos(a2) - z1*sin(a2)
z2 = sin(a1+a2) = sin(a1)*cos(a2) + cos(a1)*sin(a2) = z1*cos(a2) + y1*sin(a2)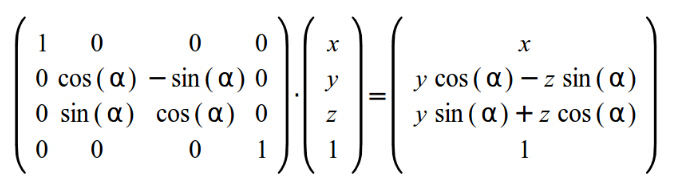
绕 Y 轴的旋转矩阵为:
z1 = cos(a1)
x1 = sin(a1)
z2 = cos(a1+a2)
x2 = sin(a1+a2)
x2 = sin(a1+a2) = sin(a1)*cos(a2) + cos(a1)*sin(a2) = x1*cos(a2) + z1*sin(a2)
z2 = cos(a1+a2) = cos(a1)*cos(a2) - sin(a1)*sin(a2) = z1*cos(a2) - x1*sin(a2)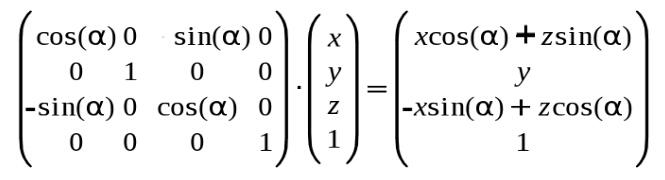







 本文详细介绍了如何使用矩阵旋转变换来实现二维平面上的点绕坐标轴旋转,并提供了具体的数学推导过程,包括绕X轴、Y轴和Z轴旋转的情况。
本文详细介绍了如何使用矩阵旋转变换来实现二维平面上的点绕坐标轴旋转,并提供了具体的数学推导过程,包括绕X轴、Y轴和Z轴旋转的情况。
















 1081
1081

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








