组合数问题I(杨辉三角)

题目描述

组合数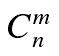表示的是从n个物品中选出m个物品的方案数。举个例子，从（1,2,3）三个物品中选择两个物品可以有(1, 2), (1, 3), (2, 3)这三种选择方法。根据组合数的定义，我们可以给出计算组合数 的一般公式:

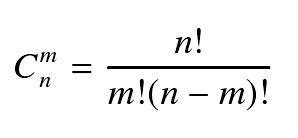
其中n! = 1×2×…×n。
小葱想知道如果给定n, m和k，对于所有的0≤i≤n,0≤ j≤min(i,m)有多少对(i, j)满足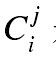是k的倍数。

输入

第一行有两个整数t, k，其中t代表该测试点总共有多少组测试数据，k的意义见【问题描述】。接下来t行每行两个整数n, m，其中n, m的意义见【问题描述】。

输出

t行，每行一个整数代表所有的。0≤i≤n,0≤ j≤min(i,m)有多少对(i, j)满足是k的倍数。

样例输入
1 2
3 3

样例输出
1

提示

在所有可能的情况中，只有以 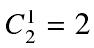是2的倍数。3≤n,m≤2000,2≤k≤2