H - New Year and the Sphere Transmission

最新推荐文章于 2022-08-31 20:01:35 发布

运行什么，直接交

最新推荐文章于 2022-08-31 20:01:35 发布

阅读量213

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/weixin_43916298/article/details/88420324

本文探讨了一个球在编号从1到n的人群中按特定规则传递的游戏。通过数学分析，找出所有可能的“趣味值”，即球触及的所有人的编号之和，并按从小到大的顺序列出这些值。文章详细解释了如何确定每次传递的有效步数，以及如何利用等差数列求和公式来计算最终的趣味值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

There are n people sitting in a circle, numbered from 1 to n in the order in which they are seated. That is, for all i from 1 to n−1, the people with id i and i+1 are adjacent. People with id n and 1 are adjacent as well.

The person with id 1 initially has a ball. He picks a positive integer k at most n, and passes the ball to his k-th neighbour in the direction of increasing ids, that person passes the ball to his k-th neighbour in the same direction, and so on until the person with the id 1 gets the ball back. When he gets it back, people do not pass the ball any more.

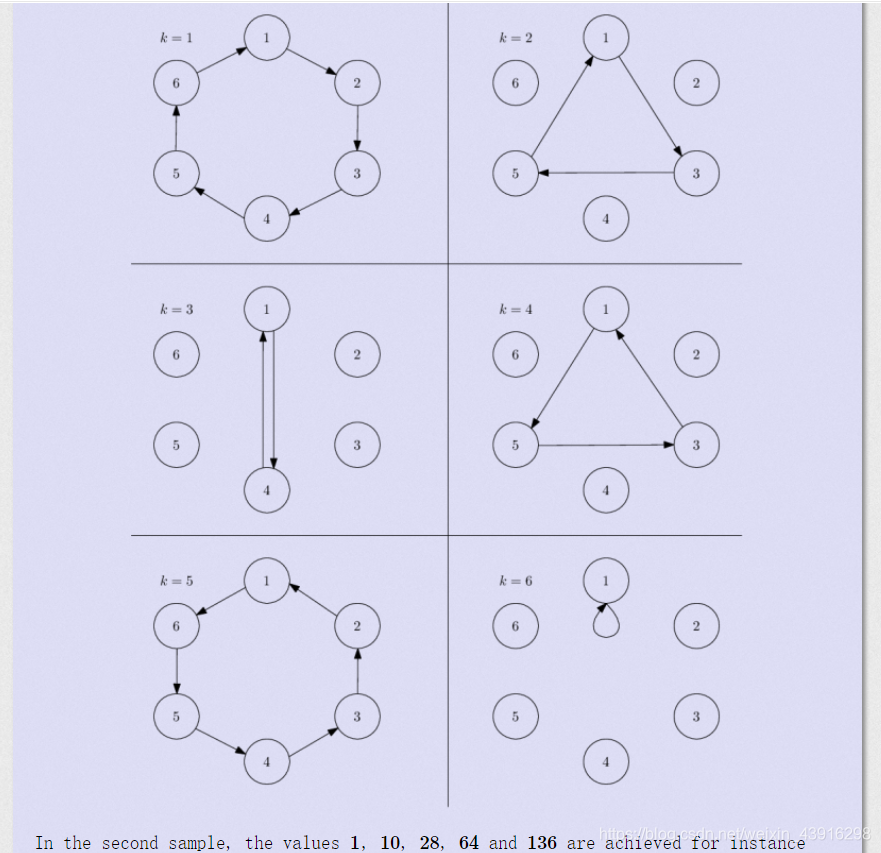
For instance, if n=6 and k=4, the ball is passed in order [1,5,3,1].

Consider the set of all people that touched the ball. The fun value of the game is the sum of the ids of people that touched it. In the above example, the fun value would be 1+5+3=9.

Find and report the set of possible fun values for all choices of positive integer k. It can be shown that under the constraints of the problem, the ball always gets back to the 1-st player after finitely many steps, and there are no more than 105 possible fun values for given n.

Input
The only line consists of a single integer n (2≤n≤109) — the number of people playing with the ball.

Output
Suppose the set of all fun values is f1,f2,…,fm.

Output a single line containing m space separated integers f1 through fm in increasing order.

Examples
Input
6
Output
1 5 9 21
Input
16
Output
1 10 28 64 136
Note
In the first sample, we’ve already shown that picking k=4 yields fun value 9, as does k=2. Picking k=6 results in fun value of 1. For k=3 we get fun value 5 and with k=1 or k=5 we get 21.

In the second sample, the values 1, 10, 28, 64 and 136 are achieved for instance for k=16, 8, 4, 10 and 11, respectively.

在这里插入图片描述

题意：
由1到n的环从一开始走每次走的个数一样，问再一次走回1所要的权值由小到大排序；
权值=路过的数的和；
首先直接走到自己最小；然后每次走一个最大
是其因子数才能重新走回去
然后就是走n-因子数=因子数
比如n=6
一次走两个或一次走四个；；

#include<stdio.h>
#include<math.h>
#include<stdlib.h>
#include <iostream>
#include<string.h>     
#include<algorithm>
#define ll long long
#define hengheng main ()
using namespace std;
int cnt=0;
ll ans[100010];
int main()
{
	ll n;
    scanf("%lld",&n);
    for(int i=1;i*i<=n;i++)  //  i为n的因子数，则n/i 也是n的因子数； 
    {
        if(n%i==0)
        {
        	ans[++cnt]=(2+n-i)*(n/i)/2;  // 等差数列 
        	ans[++cnt]=(2+n-n/i)*i/2;
		}
    }
    sort(ans+1,ans+cnt+1);
    for(int i=1;i<=cnt;i++)
        if(ans[i]!=ans[i-1])
        printf("%lld ",ans[i]);
    printf("\n");
    return 0;
}