线段树（基础）Segment Tree

目录

一.What is Segment Tree?

1.概念

2.实践

（1）建树

（2）修改区间

（3）区间查询

二.How can we use it?

例：影子的宽度

（1）题目

（2）思路

（3）思维图

（4）代码

三.sum up（总结）

四.附：关于整数的简单题

---

一.What is Segment Tree?

1.概念

线段树是一种二叉搜索树，主要用于区间查询与修改，是树状数组的一种升级版。它的时间复杂度是：①建树；②查询。先来说一说如何实践线段树。

2.实践

（1）建树

线段树中的每一个结点表示了一个区间[a,b]；根节点表示的是“整体”的区间，每一个叶子节点表示了一个单位区间。

对于每一个非叶结点所表示的区间[a,b]：左儿子表示的区间为[a,(a+b)/2]；右儿子表示的区间为[(a+b)/2+1,b]。

以下是一棵样例线段树：

附代码：

inline void build (int i, int l, int r){//i表示编号，l和r是左右区间端点
    tree[i].l = l, tree[i].r = r;
    int mid = (l + r) / 2;
    if (l == r)
        return ;
    build (i * 2, l, mid);
    build (i * 2 + 1, mid + 1, r);
}

（2）修改区间

对于修改区间，我无法给出准确的代码，但是总体思想是有的。就是找到被将被修改区间完全覆盖的区间，修改它并递归回到此区间所代表的节点的父节点。就拿上面的那个图来看，如果我要修改区间[3, 5]，那么区间[3, 3]和[4, 5]将被修改。附一个样例代码（不通用），表示把区间[l, r]每一段的值修改成1：

void insert (int i, int l, int r){
    if (tree[i].r < l || tree[i].l > r)//如果此区间与修改区间完全不相干，直接返回
        return ;
    if (tree[i].l >= l && tree[i].r <= r){//此区间被将修改区间完全覆盖
        tree[i].cnt = (tree[i].r - tree[i].l + 1) * 1;//因为是每一段，所以整个区间的总值就是看这个区间的段数有多少段
        return ;
    }
    insert (i * 2, l, r);//i * 2代表左儿子
    insert (i * 2 + 1, l, r);//i * 2 + 1代表右儿子
}

（3）区间查询

区间查询就实在是太灵活了，主要在于你是如何修改区间的。下面会有各种题目介绍区间查询的。

二.How can we use it?

例：影子的宽度

（1）题目

题目描述

桌子上零散地放着若干个盒子，盒子都平行于墙。桌子的后方是一堵墙。如图所示。现在从桌子的前方射来一束平行光， 把盒子的影子投射到了墙上。问影子的总宽度是多少？

输入

第1行：3个整数L，R，N。-100000 <=L<=R<= 100000，表示墙所在的区间；1<=N<=100000，表示盒子的个数
接下来N行，每行2个整数BL, BR，-100000 <=BL<=BR<= 100000，表示一个盒子的左、右端点（左闭右开）

输出

第1行：1个整数W，表示影子的总宽度。

样例输入

0 7 2

1 2

4 5

样例输出 

2

解释 

区间[1, 2]的长度是1；区间[4, 5]的长度也是1；建议把每个区间的右端点减1，区间的长度就可以用(r - l + 1)计算。

（2）思路

这道题的思路还是不难的。首先建树；然后边输入边修改。修改的时候要时时更新父节点，更新整个区间被覆盖的长度，最后就直接输出根节点被覆盖的长度就完了。

那么区间修改的具体操作是什么呢?有如下几种情况：

①此区间与需要修改的区间完全不相干，直接返回它的父节点。

②此区间被需要修改的区间完全覆盖，那么直接把此区间被覆盖的长度直接更新成整个区间的长度，并且直接返回到它的父节点，不需要再往下搜索。因为反正这个区间已经被覆盖了，再往下搜索它的子区间就没意义了，反正都被覆盖了。

③此区间与需要修改的区间只覆盖了一部分，就需要往下搜索，搜索它的左和右子区间。这里可以有一个优化：如果它的左区间已经被完全覆盖就不需要再搜索左区间，右区间也一样，它本身也一样。

最后就统计此区间被覆盖的区间总长就行了。

如果大家思路有点模糊，见下：

（3）思维图

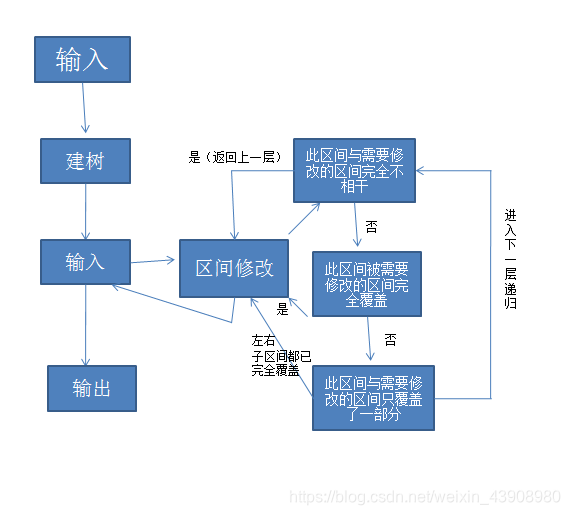
（4）代码

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define M 100005
struct node {
    int l, r, sum;
}tree[M * 6];
int n, L, R, bl, br, ans;
inline void build (int i, int l, int r){//建树
    tree[i].l = l, tree[i].r = r;
    int mid = (l + r) / 2;
    if (l == r)
        return ;
    build (i * 2, l, mid);
    build (i * 2 + 1, mid + 1, r);
}
inline void insert (int i, int l, int r){//区间修改
    if (tree[i].r < l || tree[i].l > r)
        return ;
    if (tree[i].r <= r && tree[i].l >= l){
        tree[i].sum = tree[i].r - tree[i].l + 1;
        return ;
    }
    if (tree[i].sum == tree[i].r - tree[i].l + 1)//如果此区间已被完全覆盖，就直接返回
        return ;
    if (tree[i * 2].sum < tree[i * 2].r - tree[i * 2].l + 1)//如果此区间的左子区间已被完全覆盖，就不用搜其左子区间了
        insert (i * 2, l, r);
    if (tree[i * 2 + 1].sum < tree[i * 2 + 1].r - tree[i * 2 + 1].l + 1)//如果此区间的右子区间已被完全覆盖，就不用搜其右子区间了
        insert (i * 2 + 1, l, r);
    tree[i].sum = tree[i * 2].sum + tree[i * 2 + 1].sum;//被覆盖的区间长度统计
}
int main (){
    scanf ("%d %d %d", &L, &R, &n);
    L += M;
    R += M;
    build (1, L, R - 1);
    for (int i = 1; i <= n; i ++){
        scanf ("%d %d", &bl, &br);
        bl += M;
        br += M;
        insert (1, bl, br - 1);
    }
    printf ("%d\n", tree[1].sum);
    return 0;
}

三.sum up（总结）

线段树除了这种用法，还有很多用法，比如“关于整数的简单题”（http://poj.org/problem?id=3468，有兴趣的可以做一下，我下面有正解代码）。我们要灵活运用线段树，让它发挥更大的作用。

四.附：关于整数的简单题

很简单吧，就是考区间修改和区间查询。

#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define M 100005
#define LL long long
int n, q;
LL ans, a, b, c;
char t;
struct node {
    int l, r;
    LL cnt, bj;
}tree[M * 10];
inline void Read (int &x){
    int f = 1; x = 0; char c = getchar();
    while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
    while (c >= '0' && c <= '9') {x = x * 10 + c - 48; c = getchar();}
    x *= f;
}
inline void Read1 (LL &x){
    int f = 1; x = 0; char c = getchar();
    while (c < '0' || c > '9') {if (c == '-') f = -1; c = getchar();}
    while (c >= '0' && c <= '9') {x = x * 10 + c - 48; c = getchar();}
    x *= f;
}
inline void build (int i, int l, int r){
    int mid = (l + r) / 2;
    tree[i].l = l;
    tree[i].r = r;
    if (l == r)
        return ;
    build (i * 2, l, mid);
    build (i * 2 + 1, mid + 1, r);
}
inline void lazy (int i){
    tree[i * 2].bj += tree[i].bj;
    tree[i * 2 + 1].bj += tree[i].bj;
    tree[i].cnt += tree[i].bj * (tree[i].r - tree[i].l + 1);
    tree[i].bj = 0;
}
inline void insert (int i, int l, int r, LL add){
    if (tree[i].bj)
        lazy (i);//懒标记
    if (tree[i].l > r || tree[i].r < l)
        return ;
    if (tree[i].l >= l && tree[i].r <= r){
        tree[i].cnt += add * (tree[i].r - tree[i].l + 1);
        tree[i * 2].bj += add;//懒标记
        tree[i * 2 + 1].bj += add;
        return ;
    }
    insert (i * 2, l, r, add);
    insert (i * 2 + 1, l, r, add);
    tree[i].cnt = tree[i * 2].cnt + tree[i * 2 + 1].cnt;
}
inline void count (int i, int l, int r){
    if (tree[i].bj)
        lazy (i);
    if (tree[i].l > r || tree[i].r < l)
        return ;
    if (tree[i].l >= l && tree[i].r <= r){
        ans += tree[i].cnt;
        return ;
    }
    if (tree[i].l == tree[i].r)
        return ;
    count (i * 2, l, r);
    count (i * 2 + 1, l, r);
}
int main (){
    Read (n);
    Read (q);
    build (1, 1, n);
    for (int i = 1; i <= n; i ++){
        Read1 (a);
        insert (1, i, i, a);
    }
    for (int i = 1; i <= q; i ++){
        ans = 0;
        scanf ("\n%c", &t);
        if (t == 'Q'){
            Read1 (a);
            Read1 (b);
            count  (1, a, b);
            printf ("%lld\n", ans);
        }
        else{
            Read1 (a);
            Read1 (b);
            Read1 (c);
            insert (1, a, b, c);
        }
    }
    return 0;
}