luogu P1082 同余方程

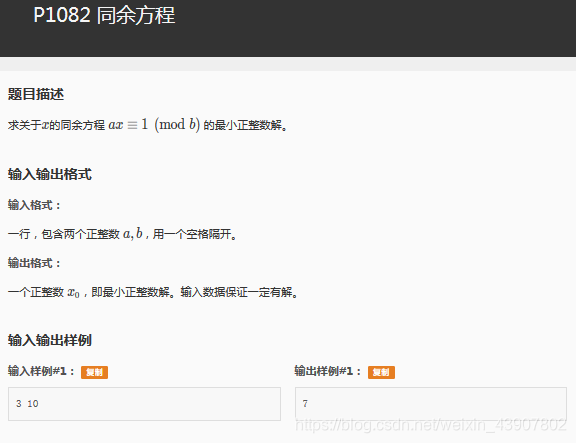
analysis

作为一道扩展欧几里德模版题，这道题涉及了一些知识点，接下来一一分析

1.裴蜀（贝祖）定理及其证明：

若a,b是整数,那么对于任意的整数x,y,ax+by都一定是gcd(a,b)的倍数，特别地，一定存在整数x,y，使ax+by=gcd(a,b)成立。

证明：
$显然gcd(a,b)\mid ax,x\in R且gcd(a,b)\mid by,y\in R$

$故gcd(a,b)|（ax+by），即一定存在整数x,y，使ax+by=k\times gcd(a,b),k\in Z成立$

$特别地当k=1时，ax+by=gcd(a,b)成立$

2.扩展欧几里德算法的核心原理

考虑如何求出$ax+by=gcd(a,b)$的某一对整数解：
根据欧几里德算法的流程，有:$gcd(a,b)=gcd(b,aMODb)$
因此构造出第二个方程：$bx+(aMODb)y=gcd(b,(aMODb))$
假设我们知道第二个方程的解x1，y1
联立两个方程：
$ax+by=bx1+(aMODb)y1$
考虑到要用已知推未知，我们将aMODb换为一个更好拆分的形式$a-a/b\ast b$ 进行研究(这里的/号是向下取整)，此时将式子按照a和b合并同类项得
$ax+by=ay1+b\times (x1-(a/b)\times y1)$
由此可得，只要x=y1,y=x1-(a/b)*y1时，得到的x和y一定可以满足上述方程$ax+by=gcd(a,b)$
因此我们可以用一个递归的过程来求x1，y1，从而求x，y

3.扩展欧几里德算法在本题的体现

由裴蜀定理，$ax+by=d存在整数解当且仅当gcd(a,b)\mid d$，而本题中d=1且一定有解，那么就可以得到$gcd(a,b)=1$，即a，b互质，因此本题就是求$ax+by=gcd(a,b)$的一组解。

4.由一组解向多组解的扩展

当然，我们将要求出来的 x,y 仅保证满足ax+by=1，而x不一定是最小正整数解。有可能太大，也有可能是负数，此时考虑如下过程：

code

#include<bits/stdc++.h>
using namespace std;
#define loop(i,start,end) for(register int i=start;i<=end;++i)
#define clean(arry,num) memset(arry,num,sizeof(arry))
#define ll long long
#define max(a,b) ((a>b)?a:b)
#define min(a,b) ((a<b)?a:b)
int a,b;
template<typename T>void read(T &x){
    x=0;char r=getchar();T neg=1;
    while(r<'0'||r>'9'){if(r=='-')neg=-1;r=getchar();}
    while(r>='0'&&r<='9'){x=(x<<1)+(x<<3)+r-'0';r=getchar();}
    x*=neg;
}
int gcd(int a,int b,int &x,int &y){
    if(b==0){
        x=1,y=0;
        return a;
    }
    int g=gcd(b,a%b,x,y);
    int t=y;
    y=x-a/b*y;
    x=t;
    return g;
}
int main(){
    #ifndef ONLINE_JUDGE
    freopen("datain.txt","r",stdin);
    #endif // ONLINE_JUDGE
    read(a),read(b);
    int xi,yi;
    int _gcd=gcd(a,b,xi,yi);
    printf("%d\n",((xi%b)+b)%b);
    return 0;
}