本文深入讲解了冒泡排序、选择排序、插入排序等经典排序算法的实现原理与优化技巧，并介绍了如何通过归并排序解决小和问题。
目录
1 冒泡排序
定义
冒泡排序(Bubble Sort)是一种最简单的交换排序方法，它通过两两比较相邻记录的关键字，如果发生逆序，则进行交换，从而使关键字小的记录如气泡一般逐渐往上 ＂漂浮＂ （左移），或者使关键字大的记录如石块一样逐渐向下“坠落” （右移）
实现1（每一趟将最大的数右移）
将整个待排序的记录序列划分成有序区和无序区，初始状态有序区为空，无序区包括所有待排序的记录。
对无序区从前向后依次将相邻记录的关键字进行比较，若逆序将其交换，从而使得关键字值小的记录向上”飘浮”（左移），关键字值大的记录好像石块，向下“堕落”（右移）。 每经过一趟冒泡排序，都使无序区中关键字值最大的记录进入有序区，对于由n个记录组成的记录序列，最多经过n-1趟冒泡排序，就可以将这n个记录重新按关键字顺序排列。
原始的冒泡排序算法 对由n个记录组成的记录序列，最多经过（n-1）趟冒泡排序，就可以使记录序列成为 有序序列，第一趟定位第n个记录，此时有序区只有一个记录；第二趟定位第n-1个记录，此时有序区有两个记录；以此类推，算法框架为：for
(int e = arr.size() - 1; e > 0; --e) { 定位第e-1个记录； }
/**
* (1) 冒泡排序（一）：从最左端往右边两两比较，每一趟将最大的数移到右边
*/
void BubbleSort(vector<int> arr ) // n为数组长度
{
if (arr.empty() || arr.size() < 2) { // 如果数组为空或者个数为1，则无需排序
return;
}
for (int i = arr.size() - 1; i > 0; --i) { // 左端区间[0,e]为无序（区间宽度逐渐减小），右端区间有序,最多n-1趟（i最大值arr.size()-1，最小值为1）排序
for (int j = 0; j < i; ++i) { // 第e趟右边e个已经有序,从最左边开始两两比较
if (arr[j] > arr[j + 1]) { // 如果前面的值比后面值大，则进行交换顺序，将大值右移
swap(arr[j],arr[j + 1]);
}
}
}
}
// 改进，加入flag，如果有某一趟没有发生交换，说明已经有序，则直接退出循环
void BubbleSort(vector<int> arr ) // n为数组长度
{
if (arr.empty() || arr.size() < 2) { // 如果数组为空或者个数为1，则无需排序
return;
}
for (int i = arr.size() - 1; i > 0; --i) { // 左端区间[0,i]为无序（区间宽度逐渐减小），右端区间有序
int flag = 0; // 是否发生交换的标志
for (int j = 0; j < i; ++j) { // 第i趟右边i个已经有序,从最左边开始两两比较
if (arr[j] > arr[j + 1]) { // 如果前面的值比后面值大，则进行交换顺序，将大值右移
swap(arr[j],arr[j + 1]);
flag = 1; // 发生了交换
}
}
if (!flag) { // 如果某一趟排序没有交换，则说明已经有序
break;
}
}
}
实现2（每一趟将最小的数左移）
将整个待排序的记录序列划分成有序区和无序区，初始状态有序区为空，无序区包括所有待排序的记录。
对无序区从后向前依次将相邻记录的关键字进行比较，若逆序将其交换，从而使得关键字值小的记录向上”飘浮”（左移），关键字值大的记录好像石块，向下“堕落”（右移）。每经过一趟冒泡排序，都使无序区中关键字值最小的记录进入有序区，对于由n个记录组成的记录序列，最多经过n-1趟冒泡排序，就可以将这n个记录重新按关键字顺序排列。
原始的冒泡排序算法 对由n个记录组成的记录序列，最多经过（n-1）趟冒泡排序，就可以使记录序列成为 有序序列，第一趟定位第1个记录，此时有序区只有一个记录；第二趟定位第2个记录，此时有序区有两个记录；以此类推，算法框架为：for (int b = 0; b < arr.size() - 1; ++b) { 定位第b+1个记录； }
//从最右端往左边两两比较，每一趟将最小的数移到左边
void BubbleSort(vector<int> arr)
{
if (arr.empty() || arr.size() < 2) { //如果数组为空或者个数为1，则无需排序
return;
}
//最多进行arr.size() - 1趟排序
for (int b = 0; b < arr.size() - 1; ++b) { //右端区间[b,arr.size()-1)为无序（区间宽度逐渐减小），左端区间有序
int flag = 0; //是否发生交换的标志
for (int j = arr.size() - 1; j > b + 1; --j) { //第b趟左边b个已经有序,从最右边开始两两比较
if (arr[j] < arr[j - 1]) { //如果前面元素比后面元素大则交换,将小值左移
swap (arr[j], arr[j - 1]);
flag = 1; //发生了交换
}
}
if (!flag) //如果某一趟排序没有交换，则说明已经有序
break; //return;
}
}
2 选择排序
/*
* (1)//简单选择排序;
* 第一次从待排序的数据元素中选出最小（或最大）的一个元素，
* 存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，
* 然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。
* 选择排序是不稳定的排序方法。
* 类比打扑克牌时，手里的牌已经排好序，每次新增时都将新增的插入到合适的位置
*/
void SimpleSelectSort(vector<int> arr)
{
if (arr.empty() || arr.size()) {
return;
}
for (int i = 0; i < arr.size() - 1; ++i) { //最多arr.size() - 1 趟排序,无序区间[i,arr.size()-1]
int minIndex = i; //每一趟将下表为i的元素初始化为最小值，其下标记为minIndex
for (int j = i + 1; j < arr.size(); ++j) { //每一趟从无序中选出最小的数,将其下标赋值给minIndex
minIndex = arr[j] < arr[minIndex] ? j : minIndex;
}
swap(arr[i], arr[minIndex]);
}
}
3 插入排序
/*
* (1) 直接插入排序
* 插入排序是一种最简单的排序方法，
* 它的基本思想是将一个记录插入到已经排好序的有序表中，
* 从而一个新的、记录数增1的有序表。
* 在其实现过程使用双层循环，外层循环对除了第一个元素之外的所有元素，
* 内层循环对当前元素前面有序表进行待插入位置查找，并进行移动。
* 类似于将新增的一张扑克牌插入到手中已经排好序的牌中的过程。
*/
void DirectInsertSort(vector<int> arr)
{
if (arr.empty() || arr.size() < 2) {
return;
}
for (int i = 1; i < arr.size() - 1; ++i) { //外层循环从第二个元素开始
for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; --j) {
swap(arr[j], arr[j + 1]); //如果新增的元素大于有序中的最后一个，则交换位置，更深层次的……
}
}
}
4 对数器的实现
对数器的概念和使用
0，有一个你想要测的方法a，
1，实现一个绝对正确但是复杂度不好的方法b，
2，实现一个随机样本产生器
3，实现比对的方法
4，把方法a和方法b比对很多次来验证方法a是否正确。
5，如果有一个样本使得比对出错，打印样本分析是哪个方法出错
6，当样本数量很多时比对测试依然正确，可以确定方法a已经正确。
#include<iostream>
#include<vector>
#include<random>
#include<cassert>
#include<algorithm>
#include<ctime>
using namespace std;
default_random_engine e;
// 自己实现插入排序
void InsertSort(vector<int> &arr) {
if (arr.size() < 2) {
return;
}
for (int i = 1; i < arr.size(); i++) {
for (int j = i - 1; j >= 0 && arr[j + 1] < arr[j]; j--) {
swap(arr[j], arr[j + 1]);
}
}
}
// for test
vector<int> generateRandomArray(int maxSize, int& size, int minValue, int maxValue) {
assert(minValue < maxValue);
size = e() % maxSize + 1;
vector<int> arr(size);
for (int i = 0; i < arr.size(); i++) {
arr[i] = e() % (maxValue - minValue) + minValue;
}
return arr;
}
// for test
vector<int> copyArray(vector<int> arr, const int n) {
vector<int> arr2(n);
arr2.assign(arr.begin(), arr.end());
return arr2;
}
// for test
void rightMethod(vector<int>& arr, const int size) {
sort(arr.begin(), arr.end());
}
// for test
bool isEqual(vector<int>& arr1, vector<int>& arr2, const int size) {
for (int i = 0; i < size; i++) {
if (arr1[i] != arr2[i])
return false;
}
return true;
}
// for test
void printArray(vector<int>& arr, const int size) {
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
cout << endl;
}
void testAlgorithm() {
int testTime = 500000;
int maxSize = 10;
int minValue = -100;
int maxValue = 100;
bool succeed = true;
clock_t startTime, endTime;
int size = 0;
startTime = clock();
for (int i = 0; i < testTime; i++) {
vector<int> arr = generateRandomArray(maxSize, size, minValue, maxValue);
vector<int> arr1 = copyArray(arr, size);
vector<int> arr2 = copyArray(arr, size);
InsertSort(arr1);
rightMethod(arr2, size);
if (!isEqual(arr1, arr2, size)) {
succeed = false;
printArray(arr2, size);
break;
}
}
cout << (succeed ? "NICE" : "FUCKED") << endl;
endTime = clock();
cout << "time cost:" << (double)(endTime - startTime) / CLOCKS_PER_SEC << "s" << endl;
}
int main()
{
testAlgorithm();
system("PAUSE");
return 0;
}
#endif
5 剖析递归行为和递归行为时间复杂度的估算
任何递归行为都可以转化为非递归行为
有些算法在处理一个较大规模的问题时，往往会把问题拆分成几个子问题，对其中的一个或多个问题递归地处理，并在分治之前或之后进行一些预处理、汇总处理。这时候我们可以得到关于这个算法复杂度的一个递推方程，求解此方程便能得到算法的复杂度。
主方法Master是用来利用分治策略来解决问题经常使用的时间复杂度的分析方法，众所周知，分治策略中使用递归来求解问题分为三步走，分别为分解、解决和合并，所以主方法的表现形式：
T [n] = aT[n/b] + f (n)（直接记为T [n] = aT[n/b] + T (N^d)）
其中 a >= 1 and b > 1 是常量，其表示的意义是n表示问题的规模，a表示递归的次数也就是生成的子问题数，b表示每次递归是原来的1/b之一个规模，f（n）表示分解和合并所要花费的时间之和。
n: 父问题的样本量
n/b: 被拆成子问题的样本量
a: 该过程发生了多少次
T(n的d次方): 除去子过程之外，剩下的过程时间复杂度是多少
解法：
①当d<log(b) a时，时间复杂度为O(n^(logb a))
②当d=log(b) a时，时间复杂度为O((n^d)*logn)
③当d>log(b) a时，时间复杂度为O(n^d)
6 归并排序
归并排序，是创建在归并操作上的一种有效的排序算法。算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。归并排序思路简单，速度仅次于快速排序，为稳定排序算法，一般用于对总体无序，但是各子项相对有序的数列。
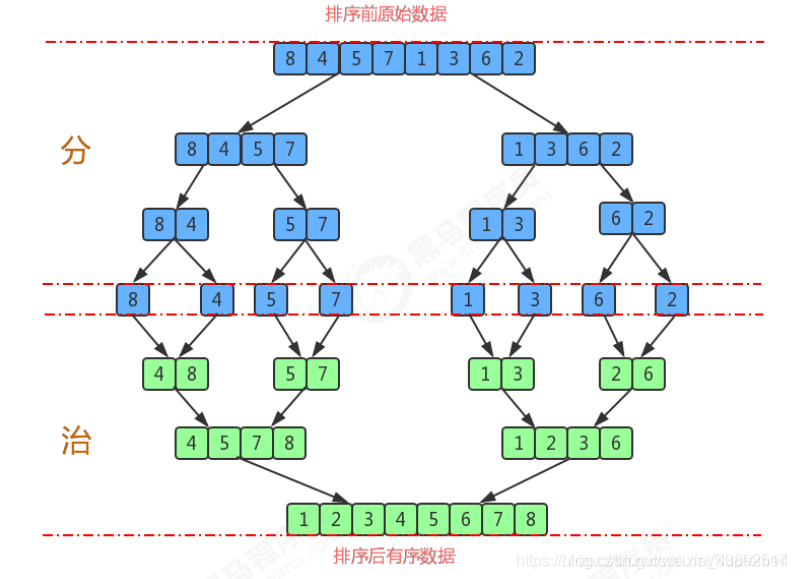
归并排序是用分治思想，分治模式在每一层递归上有三个步骤：
- 分解（Divide）：将n个元素分成个含n/2个元素的子序列。
- 解决（Conquer）：用合并排序法对两个子序列递归的排序。
- 合并（Combine）：合并两个已排序的子序列已得到排序结果。
原理
- 尽可能的一组数据拆分成两个元素相等的子组，并对每一个子组继续拆分，直到拆分后的每个子组的元素个数是1为止。
- 将相邻的两个子组进行合并成一个有序的大组；
- 不断的重复步骤2，直到最终只有一个组为止。
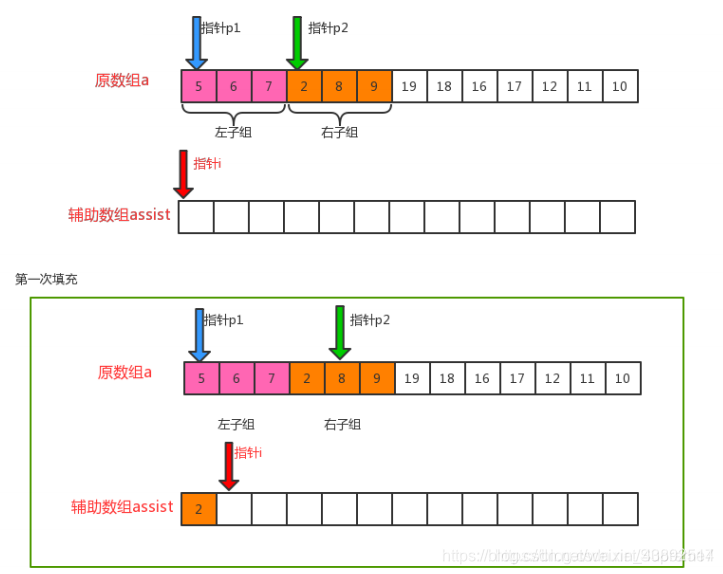
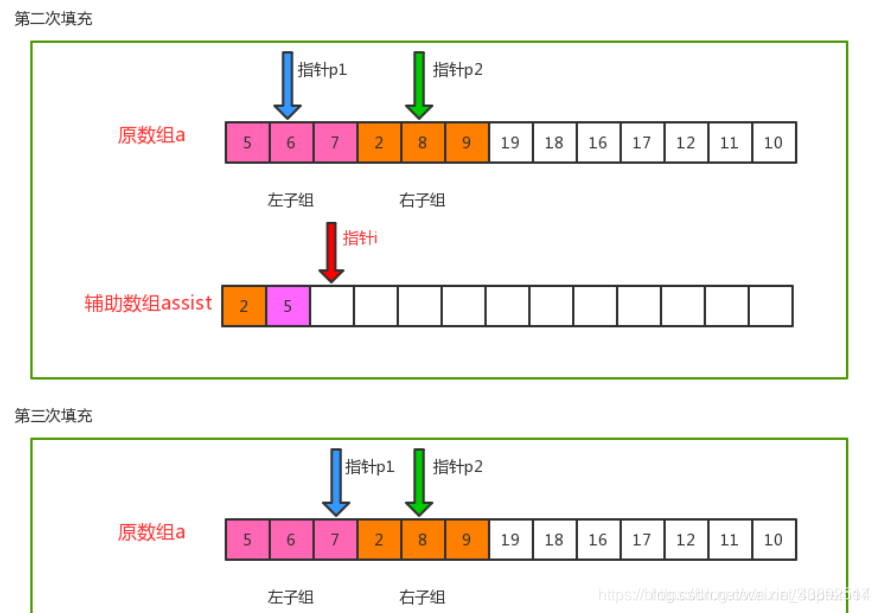
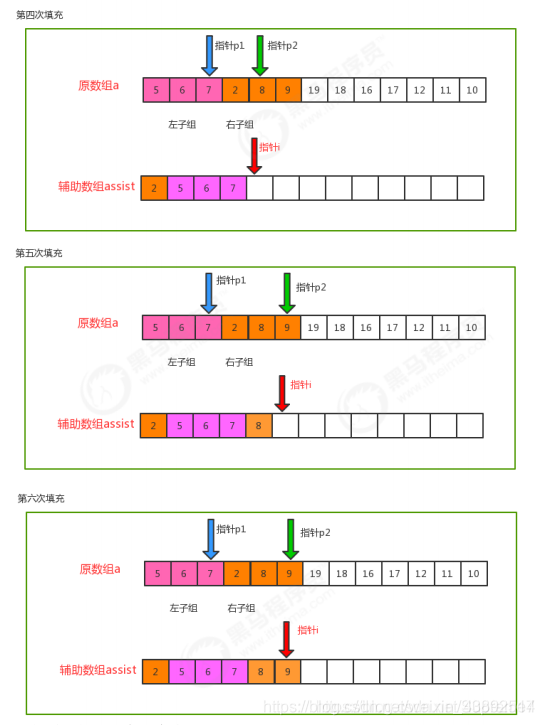
归并排序在归并的过程中，只有arr[i]<arr[i+1]的时候才会交换位置，如果两个元素相等则不会交换位置，所以它并不会破坏稳定性，归并排序是稳定的。
实现
/*
* 将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，
* 再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。
*/
void MergeSort(vector<int> arr, int l, int r);
void MergeSort(vector<int> arr)
{
if (arr.empty() || arr.size() < 2) {
return;
}
MergeSort(arr, 0, arr.size() - 1);
}
void merge(vector<int> arr, int l, int mid, int r);
void MergeSort(vector<int> arr, int l, int r)
{
if (l == r) { //递归终止条件
return;
}
int mid = l + ((r-l)>>1);
MergeSort(arr, l, mid); //T(n/2)
MergeSort(arr,mid + 1, r); //T(n/2)
merge(arr, l, mid, r); //O(N)
// T(N) = 2T(n/2) + O(N) --》时间复杂度：O(nlogn)
}
void merge(vector<int> arr, int l, int mid, int r)
{
int* helper = new int[r - l + 1]; //辅助数组，在辅助数组上排好序后拷贝到原数组,vector<int> helper(r - l + 1);
int p1 = l;
int p2 = r;
int i = 0; //helper数组索引
while (p1 <= mid && p2 <=r) {
helper[i++] = arr[p1] < arr[p2] ? arr[p1] : arr[p2];
}
//两个且必有一个越界
while (p1 <= mid) {
helper[i++] = arr[p1++];
}
while (p2 <= r) {
helper[i++] = arr[p2++];
}
for (i = 0;i < helper.size(); i++) {
arr[l+i] = helper[i];
}
delete[] helper;
}
应用–小和问题
问题：
在一个数组中，每一个数左边比当前数小的数累加起来，叫做这个数组的小和。求一个数组的小和。
例子：[1,3,4,2,5]
1左边比1小的数，没有；
3左边比3小的数，1；
4左边比4小的数，1、3；
2左边比2小的数，1；
5左边比5小的数，1、3、4、2；
所以小和为1+1+3+1+1+3+4+2=16
分析：
在归并过程中计算小和，实质是如果左数小于右数，则记录
1 3 4|2 5
/
1 3 |4 2|5
/
1|3
- 在1|3归并中，1<3，产生小和1；
- 在1 3|4归并中，p1指向1，p2指向4。1<4，记录小和1，p1指向3,3<4,继续记录小和3；
- 右侧2|5,2<5，记录小和2；
- 1 3 4 | 2 5中，p1指向1，p2指向2。1<2，则2右侧大于2的数都构成小和，记录小和2个1；p1移到3处，3>2不记录，p2右移到5,3<5，由于5右侧没有数了，所以记录小和1个3；p1继续右移，4<5，再继续记录小和1个4；
- 小和 = 1+1+3+2+21+13+1*4 = 16
实现：
result负责记录当前小和，当左侧小时，把右侧当前到右侧末尾的个数乘以左侧较小的数得到小和。
int MergeSort(vector<int> arr, int l, int r);
int SmallSum(vector<int> arr)
{
if (arr.empty() || arr.size() < 2) {
return 0;
}
MergeSort(arr, 0, arr.size() - 1);
}
int merge(vector<int> arr, int l, int mid, int r);
int MergeSort(vector<int> arr, int l, int r)
{
if (l == r) { //递归终止条件
return 0;
}
int mid = l + ((r-l)>>1);
return MergeSort(arr, l, mid) + MergeSort(arr,mid + 1, r) + merge(arr, l, mid, r);
// T(N) = 2T(n/2) + O(N) --》时间复杂度：O(nlogn)
}
int merge(vector<int> arr, int l, int mid, int r)
{
int* helper = new int[r - l + 1]; //辅助数组，在辅助数组上排好序后拷贝到原数组,vector<int> helper(r - l + 1);
int p1 = l;
int p2 = r;
int i = 0; //helper数组索引
int res = 0; //和上面归并排序中merge函数唯一的区别即是增加了返回res功能
while (p1 <= mid && p2 <=r) {
res += arr[p1] < arr[p2] ? (r - p2 + 1) * arr[p1] : 0;
helper[i++] = arr[p1] < arr[p2] ? arr[p1] : arr[p2];
}
//两个且必有一个越界
while (p1 <= mid) {
helper[i++] = arr[p1++];
}
while (p2 <= r) {
helper[i++] = arr[p2++];
}
for (i = 0;i < helper.size(); i++) {
arr[l+i] = helper[i];
}
delete[] helper;
return res;
}
扫一扫
805
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
