【leetCode】括号生成，dp，剪枝

拿到这道题的时候还挺蒙的，因为不知道该怎么去求解。然后就尝试写出前面几种结果
1、‘（）’
2、‘（（））’‘（）（）’
3、‘（（（）））’‘（）（）（）’‘（）（（））’‘（（））（）’‘（（）（））’
4、["(((())))","((()()))","((())())","((()))()","(()(()))","(()()())","(()())()","(())(())","(())()()","()((()))","()(()())","()(())()","()()(())","()()()()"]
动态规划？
有没有觉得 每一种可能性都是在子问题的一种延伸呢，比如说，2个括号的解答，是在1的基础上最外层加一个括号，或者，左边或者右边加一对括号，然后再把重复项去掉。
失败，这样会缺少可能性
当n=4的时候，出现这样的可能性，这种方法不会出现。
那大n值的解答是小n值解答的延伸这一点肯定没错
看完大佬的想法之后，发现我的想法有问题在于，我只是把一个括号放在外面考虑进去了，但是它可能同时有好多括号放在外面，就是左边。就是我之前代码中没出来的那一种，所以这就需要dp动态规划求解了，因为这个子问题会被调用好几次。

先来了解一下dp是什么东西。
首先，二分查找法大家都应该知道这是一个父问题分解成一个子问题的的算法，父问题分解为子问题的方法就称为分治。如下图所示。

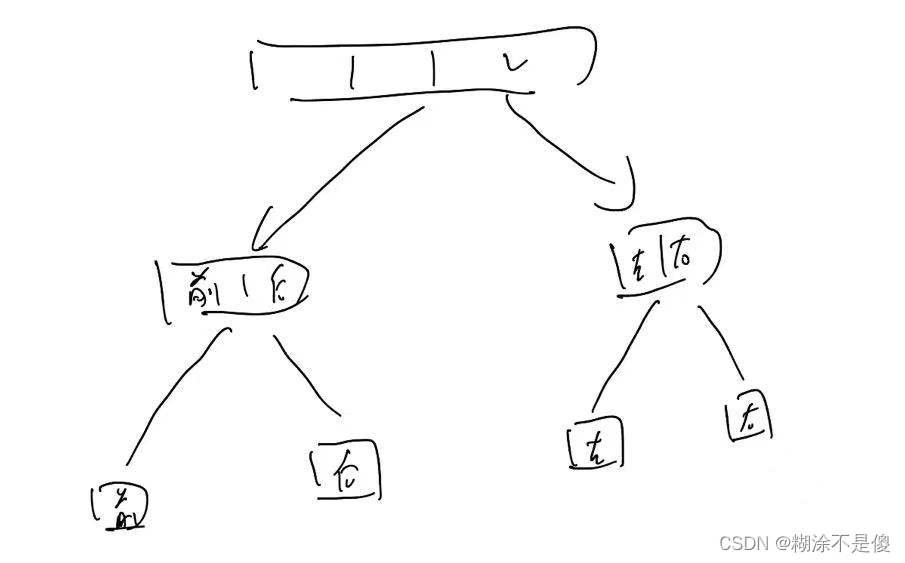
动态规划也是类似的一个父问题可以分解为子问题的一个求解，但是不同的是，它的子问题在不同的父问题中都会用到，所以因为不想多次求解子问题，故而利用一个dp数组提前记录子问题的答案，当再次求解时，直接调用子问题的答案即可。
这就是我所理解的动态规划。
动态规划最重要的点在于，对（核心）问题状态的定义以及状态转移方程的定义。
回到问题本身，既然可以进行dp，那我们就把n对括号的解答看成是在n-1对括号的解答的基础上再加一个。
增加的括号要么在这一组新增的括号内部，要么在这一组新增括号的外部（右侧）。

既然知道了 i<n 的情况，那我们就可以对所有情况进行遍历：
状态转移公式

"(" + 【i=p时所有括号的排列组合】 + “)” + 【i=q时所有括号的排列组合】

其中 p + q = n-1，且 p q 均为非负整数。

事实上，当上述 p 从 0 取到 n-1，q 从 n-1 取到 0 后，所有情况就遍历完了。

from typing import List
class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        result = []
        for i in range(0,n+1):
            re = []
            if i == 0:
                result.append([''])
            elif i==1:
                result.append(['()'])
            else:
                iter = int(i-1)
                for j in range(0,iter+1):
                    k = i-1-j
                    for o in result[j]:
                        for p in result[k]:
                            temp = '('+o+')'+p
                            if temp not in re:
                                re.append(temp)
                result.append(re)
        return result[n]
n = 3
a = Solution().generateParenthesis(n)
print(a)

除了这个方法以外，我在题解里面看到另外一种方法也挺有意思的——剪枝算法。

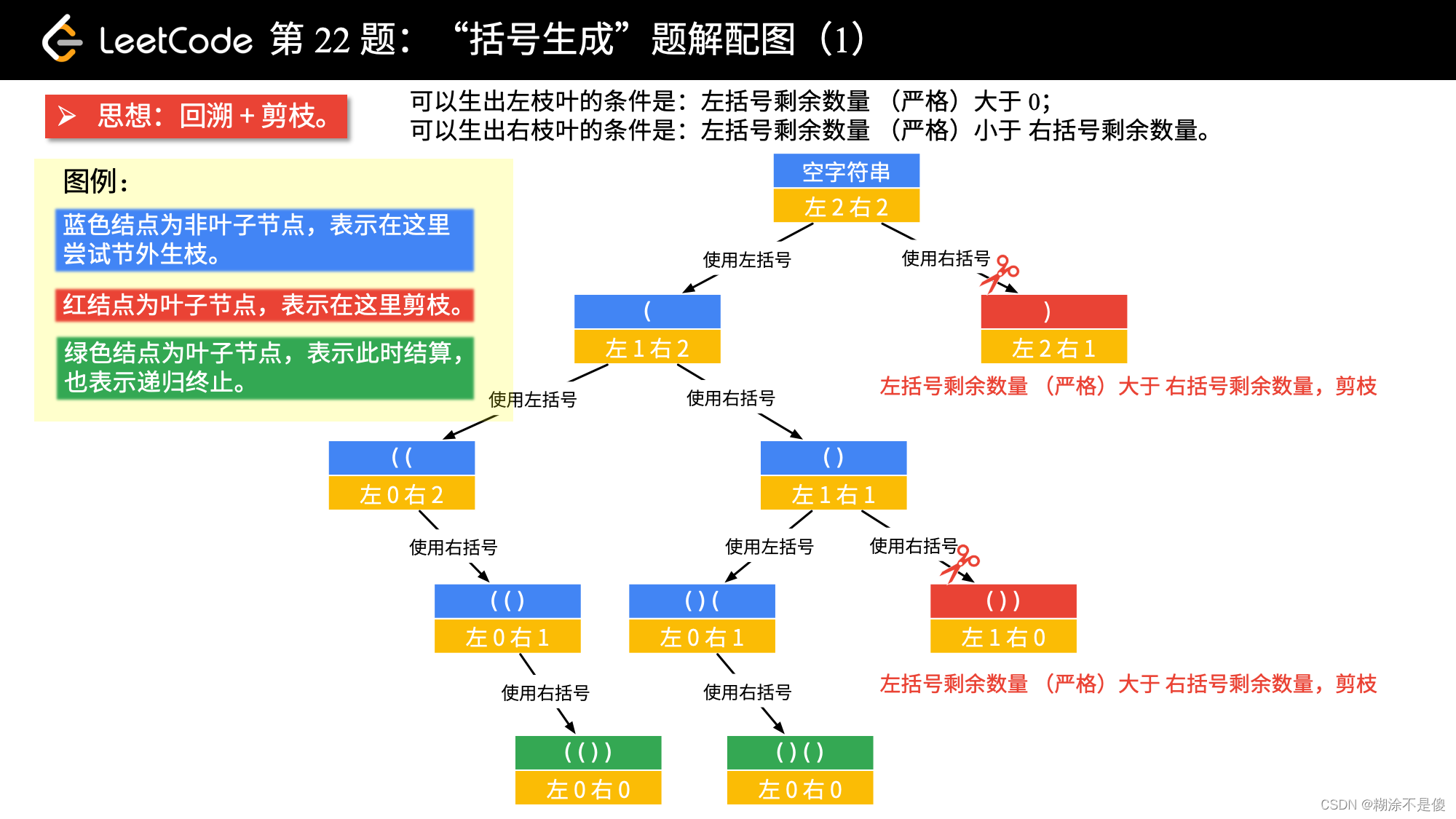
类似二分法，这个算法与二分法的区别在于，他把不可能的情况提前裁掉了，省掉了许多不必要的计算。dfs深搜与bfs广搜的区别在于下一个搜索对象从哪找，对于这道题，两种搜索方法都能用。

from typing import List
class Solution:
    def generateParenthesis(self, n: int) -> List[str]:
        res = []
        cur_str = ''
        def dfs(cur_str, left, right):
            if left == 0 and right == 0:
                res.append(cur_str)
                return
            if right < left:  #这里就是剪枝，当已经用的括号里面左括号小于有括号，说明出错了。
                return
            if left > 0:
                dfs(cur_str + '(', left - 1, right)
            if right > 0:
                dfs(cur_str + ')', left, right - 1)
        dfs(cur_str, n, n)
        return res