暑假集训日记——7.6（scc）

本文链接：https://blog.youkuaiyun.com/weixin_43870114/article/details/94854669

本文详细解析了Tarjan算法在有向图强连通分量和双连通分量中的应用，包括算法原理、实现代码与关键步骤。介绍了如何通过Tarjan算法高效地找出图中的所有强连通分量和双连通分量，适用于图论与算法设计的学习者。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

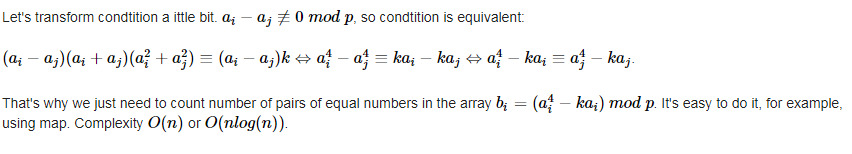
#include <bits/stdc++.h>
#define N 300500
using namespace std;
map<int,long long> mm;
int n,p,K,a[N];
long long Ans;
int main(){
	scanf("%d%d%d",&n,&p,&K);
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
		a[i]=(1ll*a[i]*a[i]%p*a[i]%p*a[i]%p-1ll*K*a[i]%p+p)%p;
		if(mm.count(a[i])){//用n-1的前缀和，来表示从n个中选两个
			Ans+=mm[a[i]];
			mm[a[i]]++;
		}
		else mm[a[i]]=1;
	}
	printf("%lld\n",Ans);
	return 0;
}

Tarjan算法

有向图强连通分量的Tarjan算法
 强连通分量及缩点tarjan算法解析
看了上面两篇感觉就差不多了
tarjan模板（缩点，求有向图强连通分量）

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, int> pli;
typedef pair<ll, ll> pll;
typedef long double ld;
#define mp make_pair

const int N=100010;
const long long INF=1e18;
const double eps=0.0000001;
const ll mod=1e9+7;

int dfn[N], low[N];///dfn[]表示深搜的步数，low[u]表示u或u的子树能够追溯到的最早的栈中节点的次序号
int sccno[N];///缩点数组，表示某个点对应的缩点值  有的写成belong
int step; ///dfs的步数
int scc_cnt;///强连通分量个数
vector<int> scc[N];///得出来的缩点，scc[i]里面存i这个缩点具体缩了哪些点
vector<int> edge[N];///存图
stack<int> S; ///判断后向边的栈

void dfs(int o)
{
    dfn[o]=low[o]=++step;
    S.push(o);
    for(int i=0;i<edge[o].size();i++)
    {
        int v=edge[o][i];
        if(!dfn[v])
        {
            dfs(v);
            low[o] = min(low[o], low[v]);
        }
        if(!sccno[v])
        {
            low[o] = min(low[o], dfn[v]);
        }
    }
    if(dfn[o]==low[o])
    {
        scc_cnt++;
        scc[scc_cnt].clear();
        while(1)
        {
            int x = S.top();
            S.pop();
            if (sccno[x] != scc_cnt) scc[scc_cnt].push_back(x);
            sccno[x] = scc_cnt;
            if (x == o) break;
        }
    }
}

void tarjan(int n)
{
    memset(sccno, 0, sizeof(sccno));
    memset(dfn, 0, sizeof(dfn));
    step = scc_cnt = 0;
    for (int i = 1; i <=n; i++)
        if (!dfn[i]) dfs(i);
}


int main()
{
   ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);


}

结论若要使得任意一棵树，在增加若干条边后，变成一个双连通图，那么
至少增加的边数 =（这棵树总度数为1的结点数 + 1 ）/ 2

点——双联通分量算法模板
注意：特判为一条边的时候

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
typedef pair<int, int> pii;
typedef pair<ll, int> pli;
typedef pair<ll, ll> pll;
typedef long double ld;
#define mp make_pair

const int N=100010;
const long long INF=1e18;
const double eps=0.0000001;
const ll mod=1e9+7;

const int maxn=1e4+10;
int bccno[maxn];///点所在的双联通分量编号--割点无意义
int iscut[maxn];///点是否是割点
int low[maxn];///low[u]表示点u及其后代能连回到的最早的祖先
int pre[maxn];///pre[u]表示点u第一次被访问到时的时间戳
int dfs_clk=0,bcc_cnt=0;
vector<int>G[maxn];
vector<int>bccp[maxn];
struct Edge{int u,v;Edge(int _u=0,int _v=0){u=_u;v=_v;}};
stack<Edge>S;
void dfs(int u,int fa){
    low[u]=pre[u]=++dfs_clk;
    int sz=G[u].size();
    int child=0;
    for(int i=0;i<G[u].size();i++){
        int v=G[u][i];
        if(!pre[v]){
            S.push(Edge(u,v));
            child++;
            dfs(v,u);
            low[u]=min(low[u],low[v]);      ///由其子孙结点更新
            if(low[v]>=pre[u]){             ///此时u为割点
                ++bcc_cnt;
                bccp[bcc_cnt].clear();
                for(;;){
                    Edge e=S.top();S.pop();
                    ///if(e.u==u&&e.v==v)break;特判为一条边时
                    if(bccno[e.u]!=bcc_cnt)
                        bccno[e.u]=bcc_cnt,bccp[bcc_cnt].push_back(e.u);
                    if(bccno[e.v]!=bcc_cnt)
                        bccno[e.v]=bcc_cnt,bccp[bcc_cnt].push_back(e.v);
                    if(e.u==u&&e.v==v)break;///遇到边(u,v)时退出
                }
            }
        }
        else if(pre[v]<pre[u]&&v!=fa)        //用反向边更新low[u]
            S.push(Edge(u,v)),low[u]=min(low[u],pre[v]);
        /*实际上也可以直接写为：
        else if(pre[v]<low[u]&&v!=f)
            S.push(Edge(u,v)),low[u]=pre[v];
        */
    }
    if(fa<0&&child==1) iscut[u]==0;
}
void Tarjan(int n)
{
    memset(pre, 0, sizeof(pre));
    memset(iscut, 0, sizeof(iscut));
    memset(bccno, 0, sizeof(bccno));
    dfs_clk = bcc_cnt = 0;
    for (int i = 1; i <=n; i++)
        if (!pre[i]) dfs(i,-1);
}


int main()
{
   ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);


}

边—双联通分量

#include <bits/stdc++.h>
using namespace std;

const int maxn = 20005;
int dfn[maxn],low[maxn],tot;
vector<int> g[maxn];
bool isB[maxn][maxn];
int n,m;

//找到桥
void tarjan(int u,int fa) {
    dfn[u] = low[u] = ++tot;
    for(int i = 0; i < (int)g[u].size(); i++) {
        int v = g[u][i];
        if(!dfn[v]) {
            tarjan(v,u);
            low[u] = min(low[u],low[v]);
            if(low[v]>dfn[u])//判断
                isB[u][v] = isB[v][u] = true;
        }
        else if(fa!=v) {
            low[u] = min(low[u],dfn[v]);
        }
    }
}

//边双连通标号
int bcc_cnt;
int bccno[maxn];
void dfs(int idx) {
    dfn[idx] = 1;
    bccno[idx] = bcc_cnt;
    for(int i = 0; i < (int)g[idx].size(); i++) {
        int v = g[idx][i];
        if(isB[idx][v])
            continue;
        if(!dfn[v])
            dfs(v);
    }
}


void find_ebcc() {
    bcc_cnt = tot = 0;
    memset(dfn,0,sizeof(dfn));
    memset(low,0,sizeof(low));
    memset(bccno,0,sizeof(bccno));
    memset(isB,0,sizeof(isB));

    for(int i = 1; i <= n; i++) {
        if(!dfn[i]) {
            tarjan(i,-1);
        }
    }
    memset(dfn,0,sizeof(dfn));
    for(int i = 1; i <= n; i++) {
        if(!dfn[i]) {
            bcc_cnt++;
            dfs(i);
        }
    }
}

int main()
{
    freopen("in.txt","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i = 0; i < m; i++) {
        int u,v;
        scanf("%d%d",&u,&v);
        g[u].push_back(v);
        g[v].push_back(u);
    }
    find_ebcc();
    puts("");
    return 0;
}