D. Good Triple

最新推荐文章于 2021-08-23 19:50:45 发布

THE END GAME

最新推荐文章于 2021-08-23 19:50:45 发布

阅读量229

点赞数

CC 4.0 BY-SA版权

分类专栏： Codeforces 思维题型/数论相关

本文链接：https://blog.youkuaiyun.com/weixin_43870114/article/details/90645619

思维题型/数论相关同时被 2 个专栏收录

59 篇文章

订阅专栏

Codeforces

49 篇文章

订阅专栏

该博客探讨了一种在数学问题中寻找满足条件的最优区间的方法。通过暴力枚举左端点，并累加右端点与给定数n的距离，来确定可能的解。当遇到覆盖情况时，选择较小的区间以获得更多的解。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

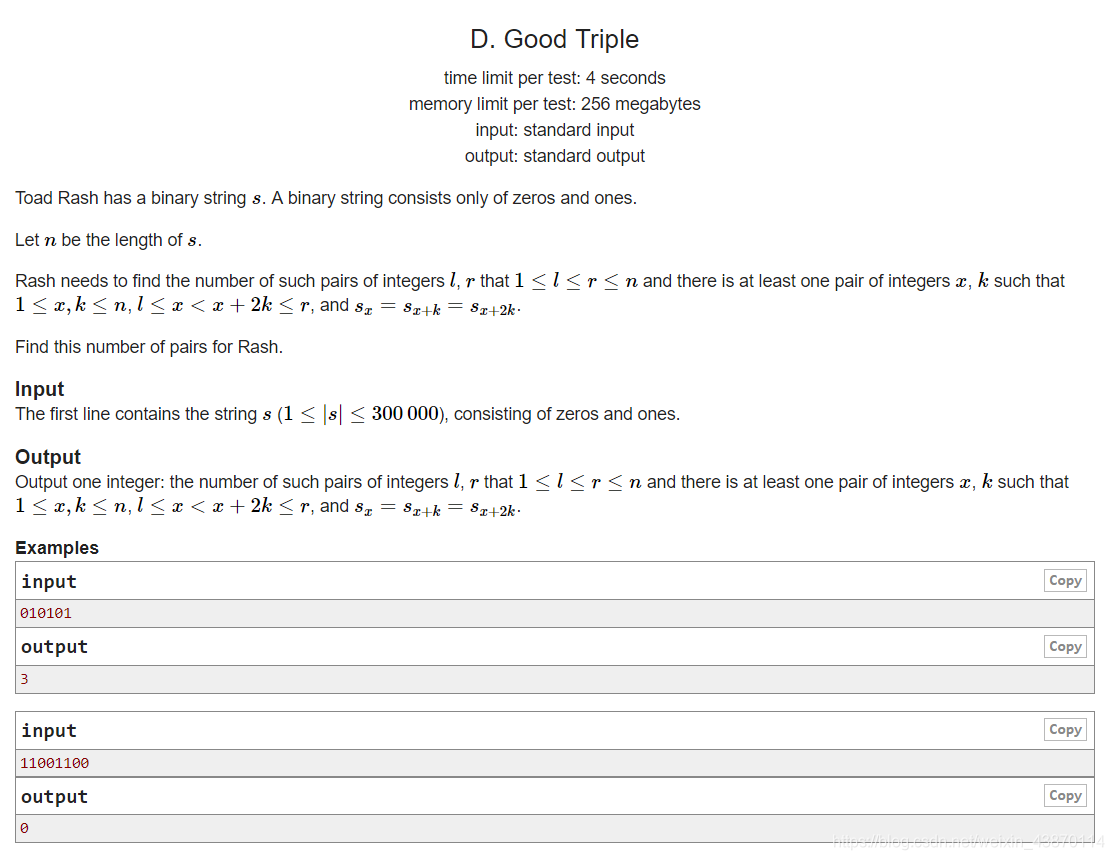
在这里插入图片描述
题解：
找到满足题意的区间，使满足l,r范围内有解
当同一范围内的区间存在覆盖的情况，取小的区间可以使解尽量多
所以暴力枚举可解
枚举左端点，依次累加右端点距n的距离即为所求解的情况

#include<algorithm>
#include<cstdio>
#include<cmath>
#include<iostream>
#include<cstring>
#include<set>
#include<map>
#include<iterator>
#include<queue>
#include<vector>
#include<string>
using namespace std;

typedef long long ll;
const int N=1e6+10;
const long long INF=1e18;
const double eps=0.0000001;
int a[N];
int n,m;
string s;

int main()
{
   ios::sync_with_stdio(false); cin.tie(0); cout.tie(0);
   cin>>s;
   int n=(int)s.length();
   ll ans=0;
   vector<int>cup(n+1,n);
   for(int i=n-1;i>=0;i--)
   {
       cup[i]=cup[i+1];
       for(int k=1;2*k+i<cup[i];k++)
       //找到满足条件的区间尽量小，才可以使l,r尽量多
       {
           if(s[i]==s[i+2*k]&&s[i]==s[i+k])
           {
              cup[i]=i+2*k;break;
           }

       }
       ans+=(n-cup[i]);
   }
   cout<<ans<<endl;


}