树-树的术语与存储结构

树：树是n(n>=0)个结点的有限集。

                  在一颗非空树中：

                         1）有且仅有一个特定的称为根(root)的结点；

                         2）当n>1时，其余结点可分为m(m>0)个互不相交的有限集T1，T2,…,Tm，其中每个集合本身又是一颗树，并且称为根的子树(subtree)。

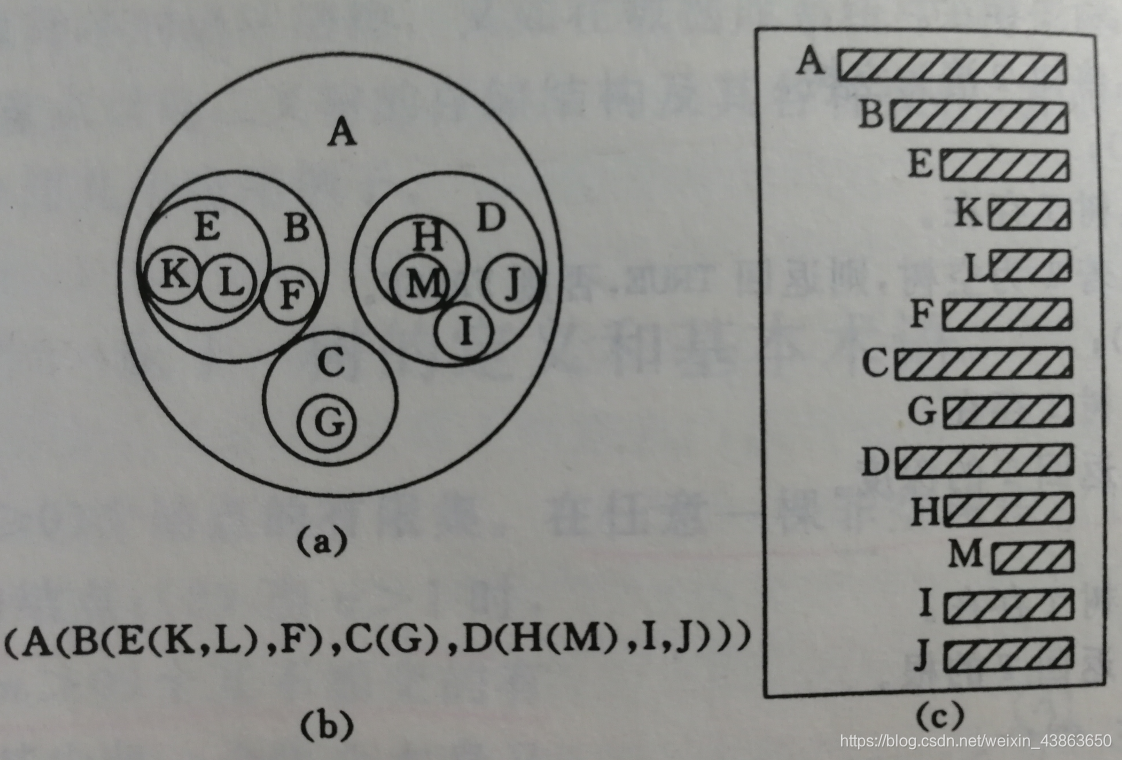
树的四种表示法：

1）树型     2）广义表     3）嵌套集合 4）凹入表示法

树形表示法

a)嵌套集合 b)广义表 c)凹入表示法

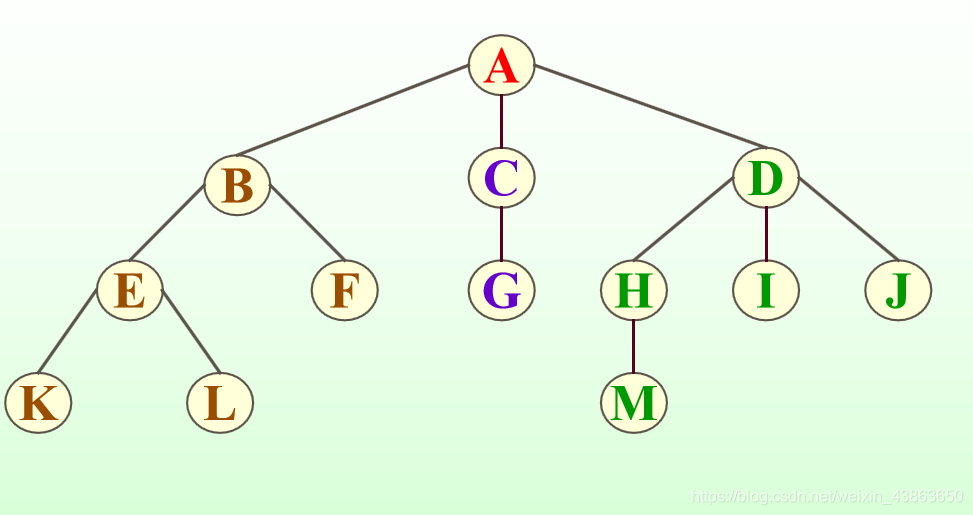
树的术语：

结点分类：

结点的度：结点具有的子树数称为该结点的度(Degree)。    

叶结点（终端结点）：度为0的结点，即没有子树的结点。    

分支结点（非终端结点）：度大于0的结点。   

内部结点：除根结点外的分支结点。    

树的度：一棵树中各个结点度数的最大值。

结点间关系：

孩子和双亲：一个结点的子树的根称为该结点的孩子；反之，该结点则称为其孩子的双亲。
兄弟：同一个双亲的孩子之间互称兄弟。
祖先：从根结点到该结点所经分支上的所有结点。
子孙：以某结点为根的子树的任一结点都称为该结点的子孙。

其他：

路径：从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
树的深度：树中结点的层次（Level）是从根结点算起的。根结点为第一层，其儿子结点为第二层。树中结点的最大层数叫做此树的深度（Depth）或高度。
有序树和无序树：若将树中结点的各子树看成是从左到右是有次序的，不能互换的，则称该树为有序树；否则称为无序树。
森林(Forest)：是m（m≥0）棵互不相交的树的集合。任何一棵非空树是一个二元组Tree = （root，F）其中：root 被称为根结点F 被称为子树森林。

树的存储结构：

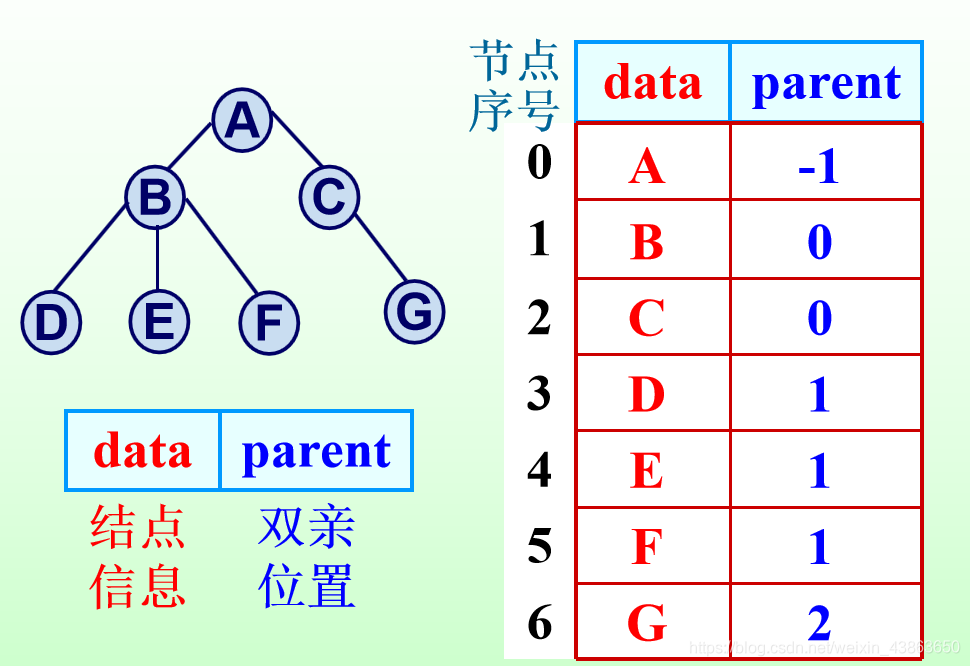
1.双亲表示法：

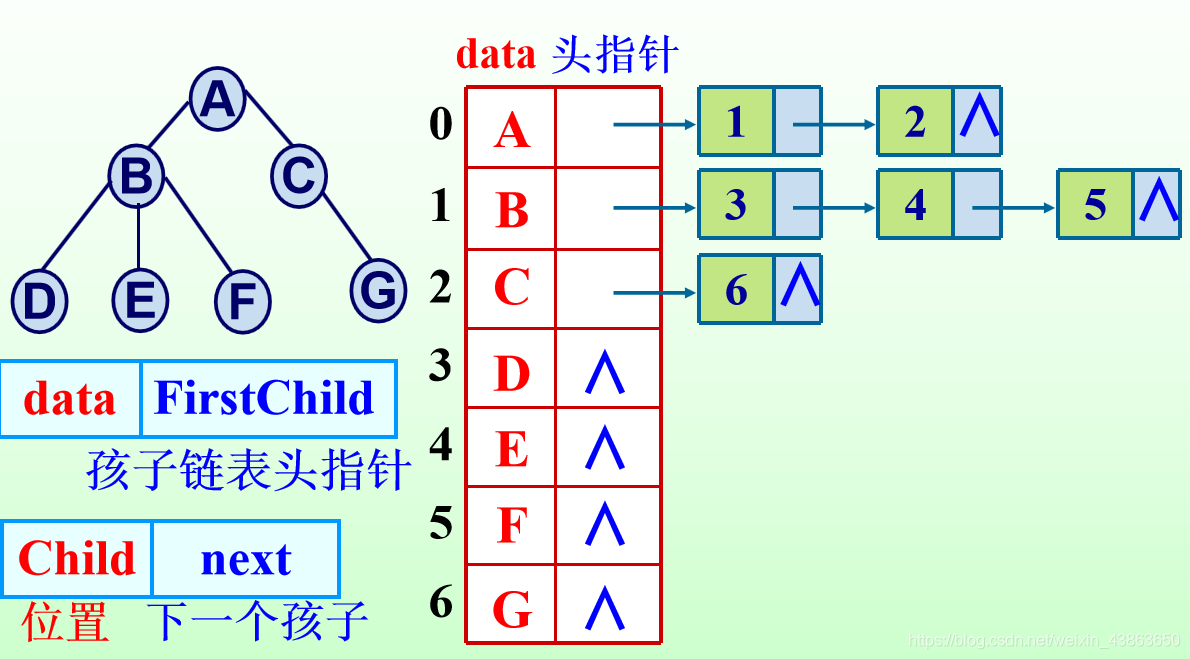
2.孩子表示法：

将每个结点的孩子结点链接构成一个单链表，称为孩子链表。将孩子链表的头指针又组成了一个顺序表。

 

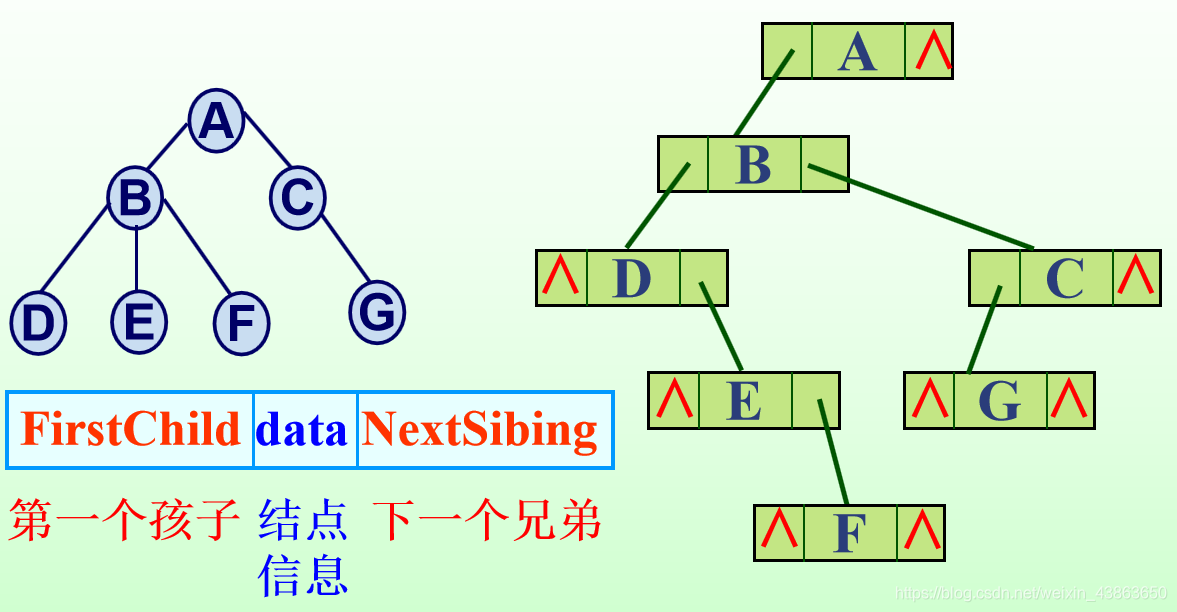
3.孩子兄弟表示法：

每个结点设有两个指针域，分别指向该结点的第一个孩子和下一个兄弟（右兄弟），又称为树的二叉链表表示法。