机器学习基础整理(第0章下) - 概率论篇

模式识别和概率的关系

机器学习算法帮助我们分析数据以及提取和识别固有模式。现实中的数据拥有不确定性 (uncertainty) 和可变性 (variability)。概率论允许我们从数据中去建模这种不确定性和可变性。这些模型功能强大，同时为统计和概率推演提供了基础。

概率

概率论是不确定事件 (non-deterministic) 的学科。我们将一场实验中的可能产出用集合S来代表:

S = { f 1 , f 2 , f 3 , . . . , f 6 } S = \{f_1, f_2, f_3, ..., f_6\} S={f1​,f2​,f3​,...,f6​}

上式是投掷骰子的结果集，每个结果的可能性为:

$p(f_i)=1/6,i=1,2,...,6$

事件 (Events) 是样本空间 (sample space) 的子集，比如:
{ e v e n } = f 2 , f 4 , f 6 \{even\} = {f_2, f_4, f_6} {even}=f2​,f4​,f6​ 以及 { o d d } = f 1 , f 3 , f 5 \{odd\} = {f_1, f_3, f_5} {odd}=f1​,f3​,f5​

当两个事件满足 $A\cap B=\varnothing$，我们可以说这两个事件是互斥的。

设我们拥有一个有限样本空间 $S$ 以及一系列事件 { A , B , . . . } \{A, B, ...\} {A,B,...}。一个概率函数 (probability function) $P$， 其为每个事件输出一个实数以满足:

• 对于所有的事件，比如说 $A$，应该满足 $0\le P(A)\le 1$.
• $P(S)=1$.
• 若 $A$ 和 $B$ 事件是互斥的，则 $P(A\cup B)=P(A)+P(B)$

若空间中的每一个样本点拥有相同的概率，我们可以称其为 等概率 (equiprobable) 或 均匀空间 (uniform space)。
我们可以使用 事件$A$ 中的 点数 (the number of points) 来得到其概率。

并集概率的求法，设我们有事件A和B:
$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

条件概率 (Conditional Probability)

事件可以依赖于其他事件，也就是说，一件事的发生会影响另一件事的概率。

给定事件E发生的情况下，事件A发生的概率如下:

$P(A|E)=\frac{P(A\cap E)}{P(E)}$

独立事件 (Independent Events)

若 $P(A|E)=P(A)$ ，则两个事件 $E$ 和 $A$ 是相互独立的，这是因为，E的发生并不会对A发生的概率产生影响。

同样的我们可以得出:

$P(A\cap E)=P(A|E)P(E)=P(A)P(E)$

互斥事件 (Mutually Exclusive Events)

若事件 $E$ 和 $A$ 是互斥的，则其中一个的发生互斥另一个的发生，即:

$P(A|E)=0$

这代表了互斥事件不是独立事件。

联合概率分布 (Joint Probability Distribution)

在这种情况下，样本空间由两个实验的结果对组成。
以下是例子说明，夏天温度和湿度的样本。

边际分布 (Marginal Distribution)

给定 $(X,Y)$ 的联合分布，其能够推导出 $X$ 和 $Y$的分布。
设 $P(x,y)$ 代表 样本点 $(x,y)$ 的概率。

此时，$P(x)$和$P(y)$被称为边际分布。
如，上一节的联合概率分布的例子中，我们有如下的边际分布:

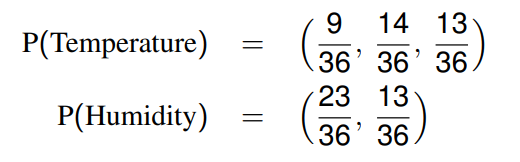
条件独立 (Conditional Independence)

假设 小明 和 小红 分别抛硬币。设 A 代表变量“小明 的投掷结果”，B 代表变量“小红 的投掷结果”。 $A$ 和 $B$ 都有两个可能的值（正面 和 反面）。没有任何争议，我们可以假设 $A$ 和 $B$ 是独立的。关于 $B$ 的证据不会改变我们对 $A$ 的信念。
现在假设 小明 和 小红 都掷相同的硬币。再次让 $A$ 代表变量 “小明 的抛掷结果”，$B$ 代表变量 “小红 的抛掷结果”。
此时再假设硬币有可能偏向正面，但我们不确定这一点。在这种情况下，$A$ 和 $B$ 不是独立的。例如，观察到 $A$ 是正面会使我们更加相信 $B$ 是正面。
在条件独立示例中，变量 $A$ 和 $B$ 都依赖于单独的变量 $C$，即“硬币偏向正面”（其值为 True 或 False）。虽然 $A$ 和 $B$ 不是独立的，但事实证明，一旦我们确定了 $C$ 的值，那么任何关于 $A$ 的证据都不能改变我们对 $B$ 的信念。 具体来说：

$P(B|C)=P(B|A,C)$

另一个例子:
假设诺曼和马丁住在伦敦市的两侧，并以完全不同的方式来上班，比如诺曼坐火车来，马丁开车。 让 $A$ 代表变量 “诺曼迟到了”（其值为 $true$ 或 $false$），同样让 $B$ 代表变量 “马丁迟到了”。 在这些情况下，假设 $A$ 和 $B$ 必须独立 是很符合直觉的。 然而，即使诺曼和马丁在不同的国家生活和工作，也可能存在一些因素（例如国际燃料短缺），这可能意味着 $A$ 和 $B$ 不是独立的。
在实践中，任何不确定性模型 (model of uncertainty) 都应考虑所有合理因素。
因此，虽然可以合理地排除撞击地球的陨石这一种特殊情况，但排除 $A$ 和 $B$ 都可能受到火车撞击 ($C$) 的影响这一事实似乎并不合理。 因为如果 C 为真，显然 $P(A)$ 会增加，但由于由事故导致的道路额外交通，$P(B)$ 也会增加。

因此，
$P(A|C)=P(A|B,C);$
$P(A,B|C)=P(A|C)\times P(B|C)$
$A$ 和 $B$ 在给定 $C$ 的时候 条件独立。在事件之间保持条件独立的典型情况是，当多个事件共享一个共同的原因时。

随机变量 (Random Variables)

随机变量为概率空间中的事件赋值，其可以看做是能输出实值的函数。
使随机变量 $X$ 能够获得 $x_1,x_2,...,x_N$
$X$的期望是:

$E(X)=\sum x_{n}p(x_n)$

期望值可以看作是随机变量的平均值。

定义一个随机变量(RV) $X$ 作为样本空间 $S$ 的 实值函数(real-valued function)，其范围由$R_X$表示。此外，若范围$R_X$是离散集，则RV是离散的。因此，离散RV $X$ 的概率函数是:
$p_X(x)=P(X=x)$
假设现在机器学习班里有十个学生，现在我们考虑他们的年龄。有三个19岁的同学，四个20岁，一个21岁，一个24岁以及一个26岁。我们要从中无重复地随机选取两个学生。
我们让 $X$ 来表示两个所选学生的平均年龄 的随机变量，并推导出 $X$ 的概率函数。
从十个学生中选择两个 的方法总数为45，因为：

而从 { 19 , 20 , 21 , 24 , 26 } \{19, 20, 21, 24, 26\} {19,20,21,24,26}中能得到的 两个年龄的平均数 的总数为10。
它们是 { 19 , 19.5 , 20 , 20.5 , 21.5 , 22 , 22.5 , 23 , 23.5 , 25 } \{19, 19.5, 20, 20.5, 21.5, 22, 22.5, 23, 23.5, 25\} {19,19.5,20,20.5,21.5,22,22.5,23,23.5,25}

45种方法中，使得平均年龄为19有三种方法 $P(X=19)=\frac{3}{45}$。而45种方法中，有$3\times 4=12$ 种方法使得平均年龄为19.5。在45种方法中，有 $6+3=9$种方法使得结果为20。使用类似的办法得到下列表格。

二阶矩和方差 (Second Moment and Variance)

取值为 $x_i$ 的随机变量 $X$ 的二阶矩是:
$E[X^2]={\sum }_i{x}_i^{2}P(x_i)$

若我们将 $X$ 的期望用 $\mu =E[X]$ 来代表，则 $X$ 的方差为，
V a r { X } = σ 2 = E [ ( X − μ ) 2 ] = ∑ i ( x i − μ ) 2 P ( x i ) Var\{X\} = \sigma^2 = E[(X - \mu)^2] = \sum_i(x_i-\mu)^2P(x_i) Var{X}=σ2=E[(X−μ)2]=∑i​(xi​−μ)2P(xi​)
其中，$\sigma$ 是 $X$ 的标准差。

两个随机变量的函数

若我们拥有两个随机变量的函数 $f(x,y)$， 且其以 $P(x,y)$ 联合概率分布。则该函数的期望为:

$E[f(x,y)]={\sum }_{R_X}{\sum }_{R_Y}f(x,y)P(x,y)$

其中 $R_X$ 和 $R_Y$ 分别是 $X$ 和 $Y$ 的范围。

期望算子 (expectation operator) 是一个线性函数，因为对于任意函数 $f_1(x,y)$$f_2(x,y)$，以及标量 ${\alpha }_1$ 和 ${\alpha }_2$，满足:
$E[{\alpha }_1{f}_1(x,y)+{\alpha }_2{f}_2(x,y)]={\alpha }_{1}E[f_1(x,y)]+{\alpha }_{2}E[f_2(x,y)]$

$X$和$Y$的期望可以被写为:

而方差 (variance) 可以被写为:

协方差 (Covariance)

$X$和$Y$的协方差被定义为:

协方差 (covariance) 是衡量 $X$ 和 $Y$ 之间 统计依赖 (statistical dependence) 程度的指标。如果 $X$ 和 $Y$ 在统计上独立，则 ${\sigma }_{xy}=0$。若 ${\sigma }_{xy}=0$，则这两个随机变量被称为 不相关 (uncorrelated)。(并不意味着不相关的变量必须在统计上独立。)

请注意，如果不相关变量具有多元正态分布 (multivariate normal distribution)，则它们在统计上是独立的。

若我们拥有关系 $Y=\alpha X$，则这代表了 $Y$ 强烈依赖 $X$，且 ${\sigma }_{xy}=\alpha {\sigma }_x$。
当协方差为正数，则 $X$ 和 $Y$ 同时增加和减少，而若负数，则当 $X$ 减少时 $Y$ 增加。

相关系数 (correlation coefficient) 被定义为:

是归一化协方差 (normalized covariance)，取值在 -1 到 +1 之间。

向量随机变量 (Vector Random Variables)

若我们拥有超过两个变量的时候，将其用向量表示更为方便。

让 $x$ 代表一个随机 $d$ 维向量，其中元素有 $x_1,x_2,...,x_d$。

联合分布 (joint distribution) 可以获得并且通常会很复杂。 如果变量在统计上是独立的，联合概率质量函数 (joint probability mass function)，$P(x)$ 如下，

边际分布 $P_{xi}(x_i)$ 是通过对其他变量的联合分布求和来获得的。

向量的期望值被定义为其元素为 原始元素的期望值 (expected values of the original components) 的向量。$d$ 维均值向量 $\mu$ (mean vector) 被定义为:

协方差矩阵被用 $\sum$ 代表，其定义为:

协方差矩阵 $\sum$ 可以被写为以下形式:
$\sum =E[(x-\mu )(x-\mu {)}^t]$

协方差矩阵是对称 (symmetric) 的，对角线元素是 x 的各个元素的方差。 它们总是正的。
不在对角线上的元素是协方差，且它们是正的或者负的。

如果变量是统计独立的，协方差是0 且 协方差矩阵是对角矩阵。

对于任意 $d$ 维向量 $w$，若其二次型 (quadratic form) $w^t\sum w>0$，则 $\sum$ 是正定矩阵 (positive definite)。若 $w^t\sum w\ge 0$，则其是正半定矩阵 (positive semi-definite)。

连续随机变量 (Continuous Random Variables)

如果随机变量可以在 连续体(continuum) 中取值，我们将其称为连续随机变量，并根据其概率密度函数 (probability density function) 对其进行描述。

概率密度函数如下

这代表了 连续随机变量 $x$ 在 范围 $(a,b)$ 中的概率。

以下式子为真

正态分布 (Normal Distributions)

正态或高斯分布的概率密度函数被定义为 (考虑单随机变量):

以下期望值可以被计算: