四种并查集

整理自：
【Leetcode】「图」的基本知识——并查集

---

并查集主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

合并（Union）：把两个不相交的集合合并为一个集合。
查询（Find）：查询两个元素是否在同一个集合中。

---

Quick Find 的「并查集」

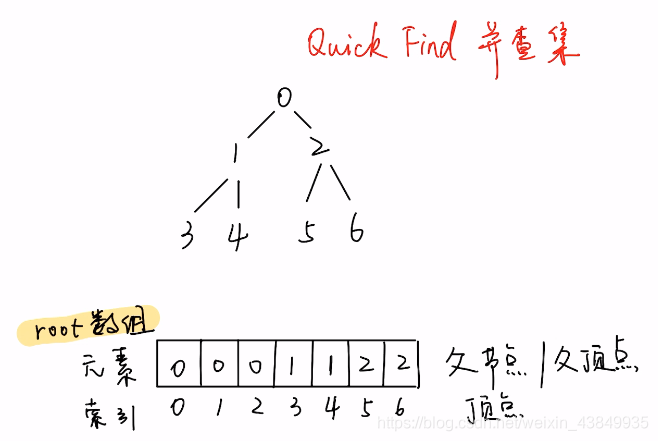
• 上图中root数组的索引是图的顶点序号，存储对应顶点的父节点序号
• 通过find()函数查询某个节点的根节点时，需要在root数组递归查询直到元素和索引相等时才算找到根节点。时间复杂度最坏可以达到O(n)。

root数组直接存储每个顶点的根节点时，find函数的时间复杂度就会降到O(1)

如果0节点和2节点之间原本是断开状态，则其root数组如下：

• 关联两个节点需要用到另一个函数——union()函数
• 将节点2与节点0关联起来，调用union(0,2)函数，可以看出，root数组中节点2,5,6的根节点需要更新为0。
• union函数首先判断0节点和2节点原本的根节点是否相同（调用find(0)和find(2)，时间复杂度为O(1)），如果不相同，union(a,b)函数会选取任一节点（a或b）作为新的根节点，遍历整个root数组，将所有以另一节点（b或a）为根节点的节点的根节点改为该节点。

Java实现代码

// UnionFind.class
public class UnionFind {
    int root[];//定义root数组

    public UnionFind(int size) {//初始化root数组，每个节点的根节点就是其自身
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    public int find(int x) {//查找x节点根节点
        return root[x];
    }
		
    public void union(int x, int y) {//关联x,y节点
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            for (int i = 0; i < root.length; i++) {
                if (root[i] == rootY) {
                    root[i] = rootX;//选取x节点作为新的根节点
                }
            }
        }
    };

    public boolean connected(int x, int y) {//判断x,y节点是否连通
        return find(x) == find(y);
    }
}

// App.java
// 测试样例
public class App {
    public static void main(String[] args) throws Exception {
        UnionFind uf = new UnionFind(10);
        // 1-2-5-6-7 3-8-9 4
        uf.union(1, 2);
        uf.union(2, 5);
        uf.union(5, 6);
        uf.union(6, 7);
        uf.union(3, 8);
        uf.union(8, 9);
        System.out.println(uf.connected(1, 5)); // true
        System.out.println(uf.connected(5, 7)); // true
        System.out.println(uf.connected(4, 9)); // false
        // 1-2-5-6-7 3-8-9-4
        uf.union(9, 4);
        System.out.println(uf.connected(4, 9)); // true
    }
}

---

Quick Union 的「并查集」

前面提到的Quick Find 的「并查集」中，find()函数时间复杂度为O(1)，主要工作量体现在union函数，union函数每次执行必然需要遍历整个root数组，因而时间复杂度为O(n)。

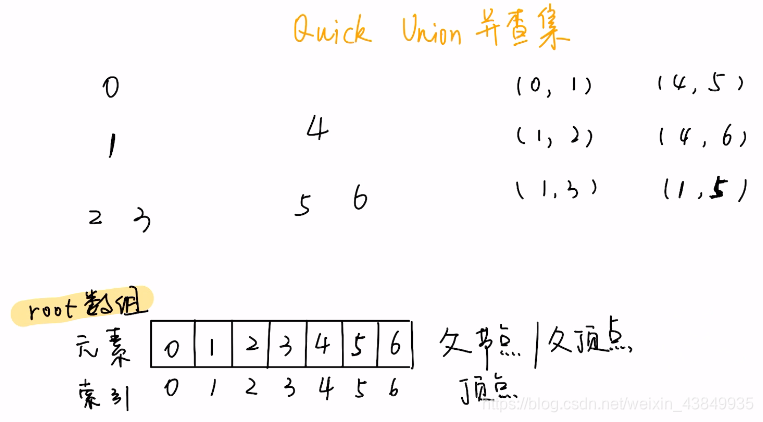
如上图所示，将六个节点按照给定的六组序列关联起来

• 前面五组节点序列关联起来后，root数组中存储的似乎也是每个节点的根节点，这和前面Quick Find 的「并查集」似乎没有区别?
• 但是进行最后一组关联时，首先我们找到1和5的根节点0和4，选取0作为新的根节点，则需要将4的根节点更新为0，但是与Quick Find 的「并查集」root数组处理不同的是，4节点的子节点5和6的根节点并不再更新，而是仍保持为4（之前4是5和6的根节点，现在只是5和6的父节点）
• 所以与Quick Find 的「并查集」的区别在于：find函数并不一定能通过root数组直接找到根节点，而需要进行递归查询，其时间复杂度最坏为O(n)，但是union函数得到了简化。

Java实现代码

public class UnionFind {
    int root[];

    public UnionFind(int size) {
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    public int find(int x) {//时间复杂度最坏为O(n)
        while (x != root[x]) {
            x = root[x];
        }
        return x;
    }

    public void union(int x, int y) {//时间复杂度最坏为O(n)
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            root[rootY] = rootX;
        }
    };

    public boolean connected(int x, int y) {//时间复杂度最坏为O(n)
        return find(x) == find(y);
    }
}

// App.java
// 测试样例
public class App {
    public static void main(String[] args) throws Exception {
        UnionFind uf = new UnionFind(10);
        // 1-2-5-6-7 3-8-9 4
        uf.union(1, 2);
        uf.union(2, 5);
        uf.union(5, 6);
        uf.union(6, 7);
        uf.union(3, 8);
        uf.union(8, 9);
        System.out.println(uf.connected(1, 5)); // true
        System.out.println(uf.connected(5, 7)); // true
        System.out.println(uf.connected(4, 9)); // false
        // 1-2-5-6-7 3-8-9-4
        uf.union(9, 4);
        System.out.println(uf.connected(4, 9)); // true
    }
}

虽然Quick Union 的「并查集」中find函数和union函数的时间复杂度都可能达到O(n)，但是Quick Union 其实还是比 Quick Find 更加高效。考虑关联N组元素的情况，Quick Union并查集最坏情况下时间复杂度为NO(n)，而Quick Find并查集的时间复杂度必然为NO(n)。

---

按秩合并的「并查集」

已经实现了 2 种「并查集」。但它们都有一个很大的缺点，这个缺点就是通过 union 函数连接顶点之后，可能所有顶点连成一条线，这就是 find 函数在最坏的情况下的样子。
新的思路是按秩合并。这里的「秩」可以理解为「秩序」。之前我们在 union 的时候，我们是随机选择 x 和 y 中的一个根节点/父节点作为另一个顶点的根节点。但是在「按秩合并」中，我们的突破点是按照「某种秩序」选择一个父节点。这里的「秩」指的是每个顶点所处的高度。我们每次 union 两个顶点的时候，选择根节点的时候不是随机的选择某个顶点的根节点，而是将「秩」大的那个根节点作为两个顶点的根节点，换句话说，我们将低的树合并到高的树之下，将高的树的根节点作为两个顶点的根节点。这样，我们就避免了所有的顶点连成一条线，这就是按秩合并优化的「并查集」。

上图中，union(0,5)执行时，Quick Union 的「并查集」中右侧和中间的两种合并方式都是可以的，区别在于中间的情况合并完成后整棵树高度变为了5，这对Quick Union 的「并查集」中的find函数是不友好的，树的高度越高，find函数查找根节点时需要递归的次数可能也就也多。因而按秩合并的核心思想就是尽可能不要构造更高的树。

Java代码实现

// UnionFind.class
public class UnionFind {
    int root[];
    int rank[];//存储每个节点的"高度"信息

    public UnionFind(int size) {
        root = new int[size];
        rank = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
            rank[i] = 1; //每个节点"高度"初始化为1，即只有自身
        }
    }

    public int find(int x) {//Quick Union并查集一样的find函数
        while (x != root[x]) {//需要递归查找直至找到根节点
            x = root[x];
        }
        return x;
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            if (rank[rootX] > rank[rootY]) {//x节点根节点高度比y节点根节点高度高
                root[rootY] = rootX;//y节点根节点的根节点成为x节点根节点
            } else if (rank[rootX] < rank[rootY]) {
                root[rootX] = rootY;
            } else {//一样高的情况
                root[rootY] = rootX;//选哪个都一样
                rank[rootX] += 1;//被选中根节点的高度要+1
            }
        }
    };

    public boolean connected(int x, int y) {
        return find(x) == find(y);
    }
}

// App.java
// 测试样例
public class App {
    public static void main(String[] args) throws Exception {
        UnionFind uf = new UnionFind(10);
        // 1-2-5-6-7 3-8-9 4
        uf.union(1, 2);
        uf.union(2, 5);
        uf.union(5, 6);
        uf.union(6, 7);
        uf.union(3, 8);
        uf.union(8, 9);
        System.out.println(uf.connected(1, 5)); // true
        System.out.println(uf.connected(5, 7)); // true
        System.out.println(uf.connected(4, 9)); // false
        // 1-2-5-6-7 3-8-9-4
        uf.union(9, 4);
        System.out.println(uf.connected(4, 9)); // true
    }
}

---

路径压缩优化的「并查集」

从前面的「并查集」实现方式中，我们不难看出，要想找到一个元素的根节点，需要沿着它的父亲节点的足迹一直遍历下去，直到找到它的根节点为止。如果下次再查找同一个元素的根节点，我们还是要做相同的操作。那我们有没有什么办法将它升级优化下呢？

答案是可以的！如果我们在找到根节点之后，将所有遍历过的元素的父节点都改成根节点，那么我们下次再查询到相同元素的时候，我们就仅仅只需要遍历两个元素就可以找到它的根节点了，这是非常高效的实现方式。那么问题来了，我们如何将所有遍历过的元素的父节点都改成根节点呢？这里就要拿出「递归」算法了。这种优化我们称之为「路径压缩」优化，它是对 find 函数的一种优化。

• 上图中，原本形成一条链路的情况下，执行find(5)需要5次递归寻找父节点，再执行find(4)时，还是需要4次递归寻找过程。而如果在find(5)的过程中，可以将2，3，4，5节点都直接与0节点关联起来，再执行find(4)时就可以直接得到4的根节点是0。
• 要实现上述设想，需要用到递归操作，每次执行find(x)时，如果x!=root[x]即x根节点不是自身时，就要递归调用find(root[x])并将find(root[x])返回值赋值给root[x]，即root[x]=find(root[x])。
• 这样在寻找根节点的过程中，x节点到其根节点路径上的所有节点的父节点（root数组存储的是父节点不是根节点，因而更改父节点其实就是将该节点直接与这个父节点关联起来）都被更新为x的根节点，它们寻找根节点时就可以一步到位直接找到。

Java代码实现

// UnionFind.class
public class UnionFind {
    int root[];

    public UnionFind(int size) {
        root = new int[size];
        for (int i = 0; i < size; i++) {
            root[i] = i;
        }
    }

    public int find(int x) {
        if (x == root[x]) {
            return x;
        }
        return root[x] = find(root[x]);
    }

    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);
        if (rootX != rootY) {
            root[rootY] = rootX;
        }
    };

    public boolean connected(int x, int y) {
        return find(x) == find(y);
    }
}

// App.java
// 测试样例
public class App {
    public static void main(String[] args) throws Exception {
        UnionFind uf = new UnionFind(10);
        // 1-2-5-6-7 3-8-9 4
        uf.union(1, 2);
        uf.union(2, 5);
        uf.union(5, 6);
        uf.union(6, 7);
        uf.union(3, 8);
        uf.union(8, 9);
        System.out.println(uf.connected(1, 5)); // true
        System.out.println(uf.connected(5, 7)); // true
        System.out.println(uf.connected(4, 9)); // false
        // 1-2-5-6-7 3-8-9-4
        uf.union(9, 4);
        System.out.println(uf.connected(4, 9)); // true
    }
}

---

总结

• Quick Union并查集比Quick Find并查集要高效

• 按秩合并、路径压缩分别是对Quick Union并查集的union函数和find函数的改进