斯特林数详解：第一类与第二类-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_43849488/article/details/104118392

本文介绍了斯特林数的两类概念，包括无标号轮换和无标号集合，通过实例展示了它们的计数原理。还探讨了斯特林数的通项、递推关系和特殊值，并提到了快速幂在斯特林数中的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

通俗易懂的斯特林数介绍

定义
- 第一类斯特林数
- 第二类斯特林数
性质

定义

第一类斯特林数

将 $n$ 个元素分成 $m$ 个无标号的轮换 $\begin{bmatrix}n\\m\end{bmatrix}$
什么叫轮换？
就是把一堆数放在一个圈上，如果可以通过旋转使得圈上的每个位置上数都和另一个圈上的数是相等的，那么这两个圈等价（意思就是它们是同一个轮换）
比如，现在有三个轮换：
在这里插入图片描述
第一个轮换和第二个轮换是等价的，第一个和第三个轮换不是等价的
那么，什么叫无标号的轮换？
就是如果一堆轮换调换顺序后和另一堆轮换完全相同（所有对应的轮换等价），那么这两堆轮换就是等价的
比如，现在有两堆轮换：
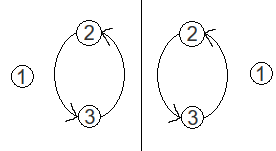
在这里插入图片描述
第一堆轮换和第二堆轮换完全相同，是等价的
为了让大家更了解第一类斯特林数，我们举一个例子： $\begin{bmatrix}3\\2\end{bmatrix}=3$
三种方法如下：

第一类斯特林数还有另一种定义，就是 $\prod \limits_{i=0}^{n-1}(x-i)$ 的 $m$ 次项系数叫 $\begin{bmatrix}n\\m\end{bmatrix}$

第二类斯特林数

将 $n$ 个元素分成 $m$ 个无标号的集合 $\begin{Bmatrix}n\\m\end{Bmatrix}$
上面我们已经解释过了无标号的意思，相信大家都知道无标号集合的意思了
为了让大家更了解第二类斯特林数，我们举一个例子： $\begin{Bmatrix}3\\2\end{Bmatrix}=3$
三种方法如下：

${\{1\},\{2,3\}\}$
${\{2\},\{1,3\}\}$
${\{3\},\{1,2\}\}$

性质

通项

第一类斯特林数貌似没有通项公式（或者是没用或者我太菜了不知道）
第二类斯特林数的通项为 $\begin{Bmatrix}n\\m\end{Bmatrix}=\frac{1}{m!}\sum \limits_{i=0}^m(-1)^i\binom{m}{k}(m-i)^n$ 貌似也没什么用……我不会证……记住就好了~~我好像也记不住？？？~~

递推

第一类斯特林数

$\begin{bmatrix}n\\m\end{bmatrix}=(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}+\begin{bmatrix}n-1\\m-1\end{bmatrix}$
证明：假如 $n - 1$ 个元素构成了 $m - 1$ 个无标号的轮换，第 $n$ 个元素独自构成一个无标号的轮换，有 $\begin{bmatrix}n-1\\m-1\end{bmatrix}$ 种方法。如果 $n - 1$ 个元素构成了 $m$ 个无标号的轮换，将第 $n$ 个元素插入到任意元素的左边，有 $(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}$ 种方法
$\therefore \begin{bmatrix}n\\m\end{bmatrix}=(n-1)\begin{bmatrix}n-1\\m\end{bmatrix}+\begin{bmatrix}n-1\\m-1\end{bmatrix}$

第二类斯特林数

$\begin{Bmatrix}n\\m\end{Bmatrix}=m\begin{Bmatrix}n-1\\m\end{Bmatrix}+\begin{Bmatrix}n-1\\m-1\end{Bmatrix}$
证明：假如 $n - 1$ 个元素构成了 $m - 1$ 个无标号的集合，第 $n$ 个元素独自构成一个无标号的集合，有 $\begin{Bmatrix}n-1\\m-1\end{Bmatrix}$