【例题描述】
李林发现每个大于5的素数的倒数都可以化为一个循环小数,例如:1/7可以转化为0.(142857),1/13可化为0.0(76923)。编程显示所有素数的循环小数。
#include<iostream>
using namespace std;
int p[1000];
int ans[1000];
int t;
void prim()
{
int i;
for(i=2;i<100;i++)
{
if(ans[i])
continue;
p[++t]=i;
int j=i+i;
while(j<100)
ans[j]=1,j+=i;
}
}
int main()
{
int i,s;
int flag=0;
int sum[100];
sum[0]=1;
int aum[100];
prim();
for(i=4;i<=t;i++)
{
s=1;
flag=1;
k=0;
cout<<"0.";
while(1)
{
a=10*s/p[i];
sum[k]=10%p[i];
s=sum[k];
//cout<<a;
for(int j=0;j<k;j++)
if(s==sum[i])
flag=1;
if(falg==1)
break;
cout<<a;
}//while
cout<<endl;
}//for
}
结果如下
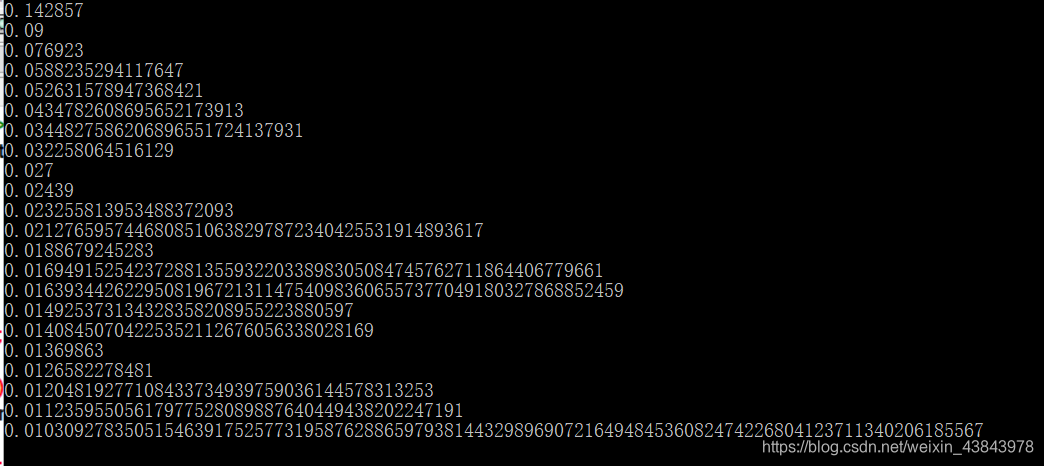







 该博客探讨了一个有趣的数学现象,即大于5的素数的倒数总是表现为循环小数。通过举例1/7等于0.142857循环和1/13等于0.076923循环,博主引导读者理解这一规律,并鼓励编程验证所有素数的循环小数形式。
该博客探讨了一个有趣的数学现象,即大于5的素数的倒数总是表现为循环小数。通过举例1/7等于0.142857循环和1/13等于0.076923循环,博主引导读者理解这一规律,并鼓励编程验证所有素数的循环小数形式。
















 1940
1940

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








