洛谷P1140 相似基因

题目描述

转的洛谷题解@my亦客♂ ~写的很清楚了

dp[i][j]代表的是，第一个碱基序列的第i位对应到第二个碱基的第j位的最大值是多少

7 AGTGATG
5 GTTAG

当i=2，j=1时 也就是AG对应G 这个状态可以由这三个状态更新

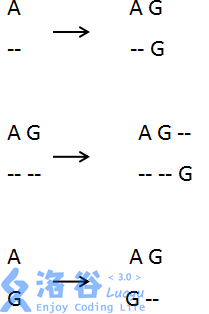
状态更新也就是，直接匹配、第一个碱基序列加一个空格、第二个碱基序列加一个空格，这三个状态。

细节问题：

1. 可以用map把碱基之间的相似度处理，也可以用数字代替
2. 要把dp[0][j]和dp[i][0]预处理
3. 答案可能为负值所以dp数组要初始为一个较大的负值

#include<iostream>
#include<algorithm>
using namespace std;
const int N=1e2+50;
int dp[N][N]; 
int la,lb,a[N],b[N];
int v[6][6]={   
                {0,0,0,0,0,0},
                {0,5,-1,-2,-1,-3},
                {0,-1,5,-3,-2,-4},
                {0,-2,-3,5,-2,-2},
                {0,-1,-2,-2,5,-1},
                {0,-3,-4,-2,-1,0}
            };
int main()
{
    for(int i=1;i<=N;i++)
    {
        for(int j=1;j<=N;j++)
        {
            dp[i][j]=-1e6;
        }
    }
    cin>>la;
    for(int i=1;i<=la;i++)
    {
        char x;
        cin>>x;
        if(x=='A') a[i]=1;
        if(x=='C') a[i]=2;
        if(x=='G') a[i]=3;
        if(x=='T') a[i]=4;
    }
    cin>>lb;
    for(int i=1;i<=lb;i++)
    {
        char x;
        cin>>x;
        if(x=='A') b[i]=1;
        if(x=='C') b[i]=2;
        if(x=='G') b[i]=3;
        if(x=='T') b[i]=4;
    }
    for(int i=1;i<=la;i++)
    {
        dp[i][0]=dp[i-1][0]+v[a[i]][5];
    }
    for(int i=1;i<=lb;i++)
    {
        dp[0][i]=dp[0][i-1]+v[5][b[i]];
    }
    for(int i=1;i<=la;i++)
    {
        for(int j=1;j<=lb;j++)
        {
            dp[i][j]=max(dp[i][j],dp[i-1][j]+v[a[i]][5]);//第一个碱基序列加空格
            dp[i][j]=max(dp[i][j],dp[i][j-1]+v[5][b[j]]);//第二个碱基序列加空格
            dp[i][j]=max(dp[i][j],dp[i-1][j-1]+v[a[i]][b[j]]);//直接匹配
        }
    }
    cout<<dp[la][lb];
    return 0;
}