作者:BerenCamlost
参考资料:
第四章 FFT
4.1 DFT运算量和FFT运算量对比
- DFT: N 2 N^2 N2次复乘, N ( N − 1 ) N(N-1) N(N−1)次复加
- FFT:
N
2
l
o
g
2
N
\frac{N}{2}log_2N
2Nlog2N次复乘,
N
l
o
g
2
N
Nlog_2N
Nlog2N次复加
- 其中FFT中的N为2的整次幂
4.2 按时间抽取的基2 - FFT原理
4.2.1 算法原理
{ X [ k ] = G [ k ] + W N k H [ k ] k = 0 , 1 , 2... N 2 − 1 X [ k + N 2 ] = G [ k ] − W N k H [ k ] k = 0 , 1 , 2... N 2 − 1 \left\{\begin{matrix} X[k]=G[k]+W_N^kH[k] & k=0,1,2...\frac{N}{2}-1\\ X[k+\frac{N}{2}]=G[k]-W_N^kH[k] & k=0,1,2...\frac{N}{2}-1 \end{matrix}\right. {X[k]=G[k]+WNkH[k]X[k+2N]=G[k]−WNkH[k]k=0,1,2...2N−1k=0,1,2...2N−1
- 其中N为2的整次幂
4.2.2 蝶形算法
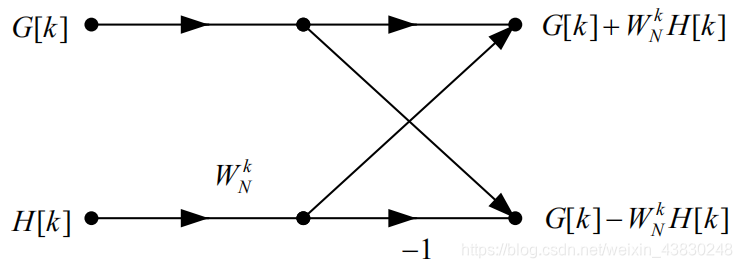
- 蝶形算法和上面的公式是同一个东西的不同表现形式。
4.3 按时间抽取的FFT流图
- 这里以16点FFT流图为例进行解释(注意这个图的WN标注的位置可能有些奇怪)
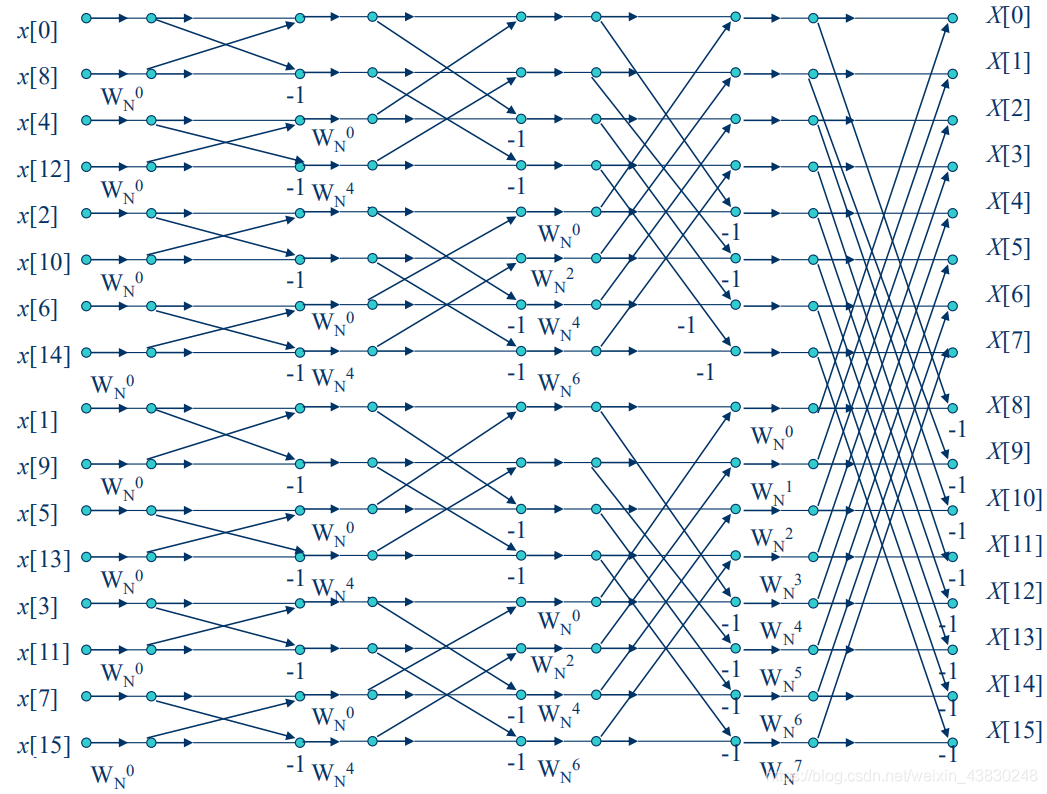
4.3.1 算法原理
由蝶形构成基本运算单元,每个流图共有M级,每一竖列有N/2个蝶形,于是得到公式 M = l o g 2 N M=log_2N M=log2N
4.3.2 原位运算
由于DFT算法的限制,导致源数据将作为每一次运算的操作数,这使得储存容量的要求很大。而FFT算法,从蝶形图中可以看出,下一个蝶形的数据源和上一次的数据源是不同的,所以可以把每一次蝶形运算得到的数据直接存放在原来的存储区域,大大减小了存储容量的要求。
4.3.3 序数重排
可以看到,FFT的结果值是按顺序排列的,如果把计算结果k的二进制和数据源的n的二进制相比较,可以发现如下规律:
| 数据源顺序 | 二进制 | 二进制 | FFT顺序 |
|---|---|---|---|
| 0 | 0000 | 0000 | 0 |
| 8 | 1000 | 0001 | 1 |
| 4 | 0100 | 0010 | 2 |
| 12 | 1100 | 0011 | 3 |
| 2 | 0010 | 0100 | 4 |
| 10 | 1010 | 0101 | 5 |
| 6 | 0110 | 0110 | 6 |
| 14 | 1110 | 0111 | 7 |
等等……
可以发现前后两个数的二进制是正好反过来的。
4.3.4 系数的确定
随缘
























 1123
1123

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








