神经网络
Neural Networks:Representation
模型表达I:Model representation I
单个神经元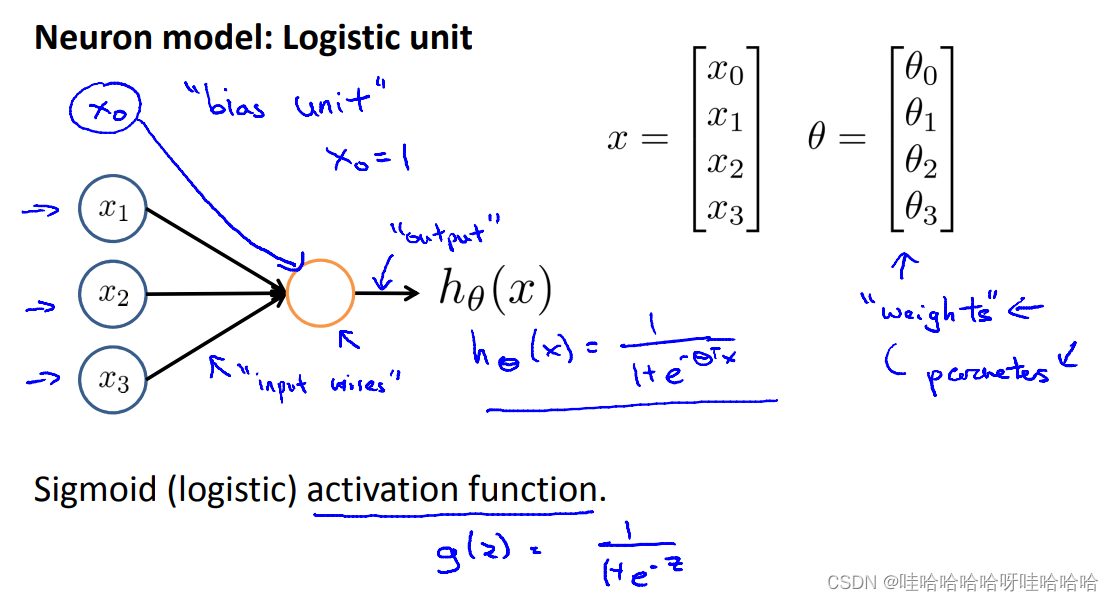 树突:input wires 轴突:output wires
树突:input wires 轴突:output wires
神经元:逻辑单元
parameter:weight权重
x0:bias unit \ bias neuron(偏置单元\偏置神经元)
Sigmoid(logistic) activation function :non-linearity非线性函数g(z)
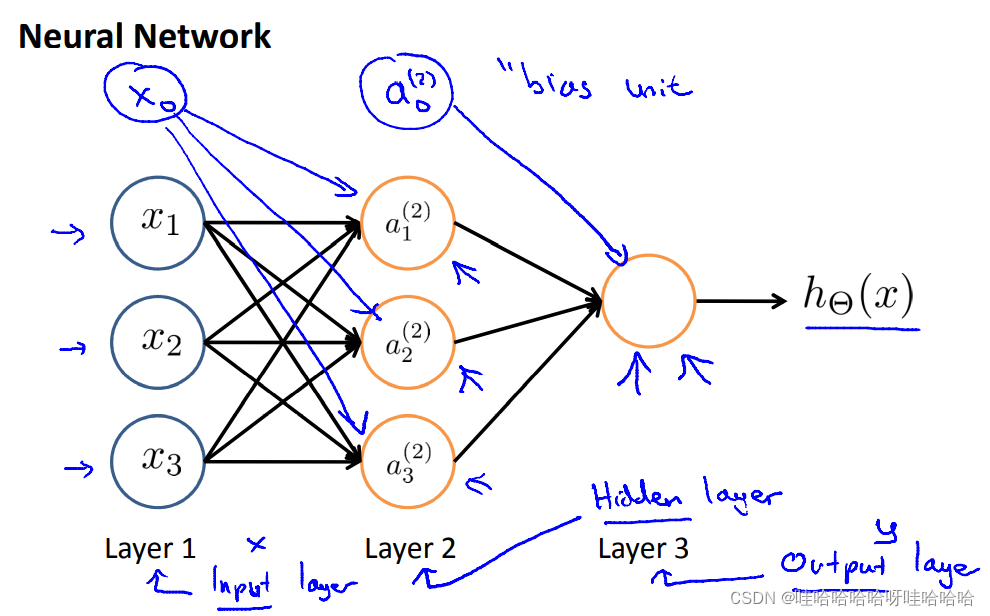 神经网络:a group of these different neurons strung togther.
神经网络:a group of these different neurons strung togther.
即一组神经元连接在一起的集合。
典型的三层神经网络:输入层、隐藏层、输出层。
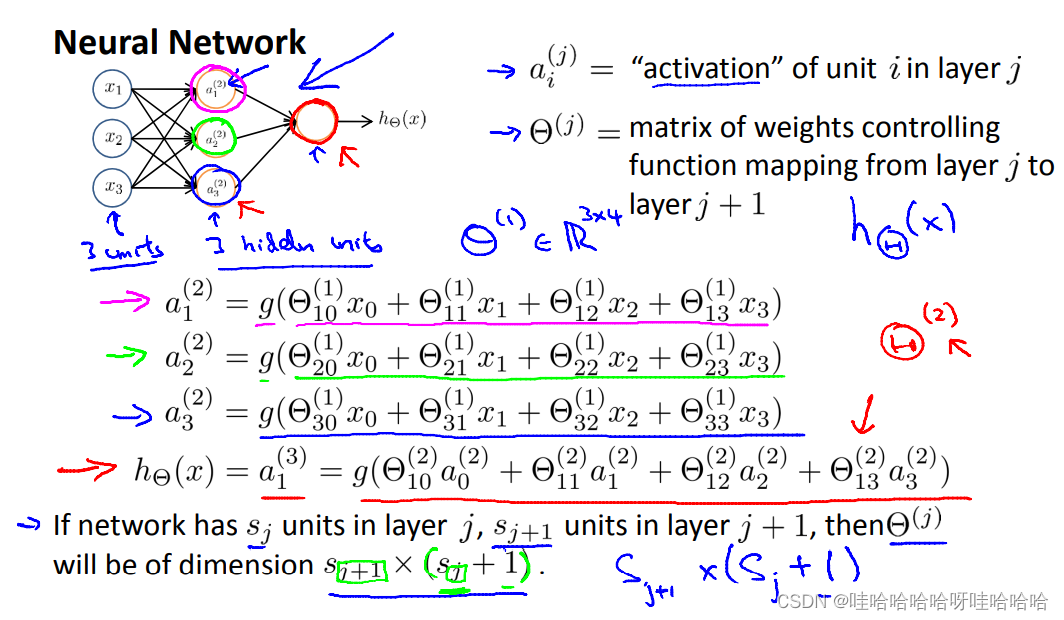
ai(j)a_i^{(j)}ai(j):第 j 层的第 i个激活项 。(“activation" of unit i in layer j”)
Θ(j):从第 j层( units:sjs_jsjj)到第 j+1层( units: sj+1s_{j+1}sj+1)的权重矩阵,
维数: sj+1×(sj+1)s_{j+1}\times (s_j+1)sj+1×(sj+1)
模型表达II:Model representation II
Forward propagation:向前传播向量化实现
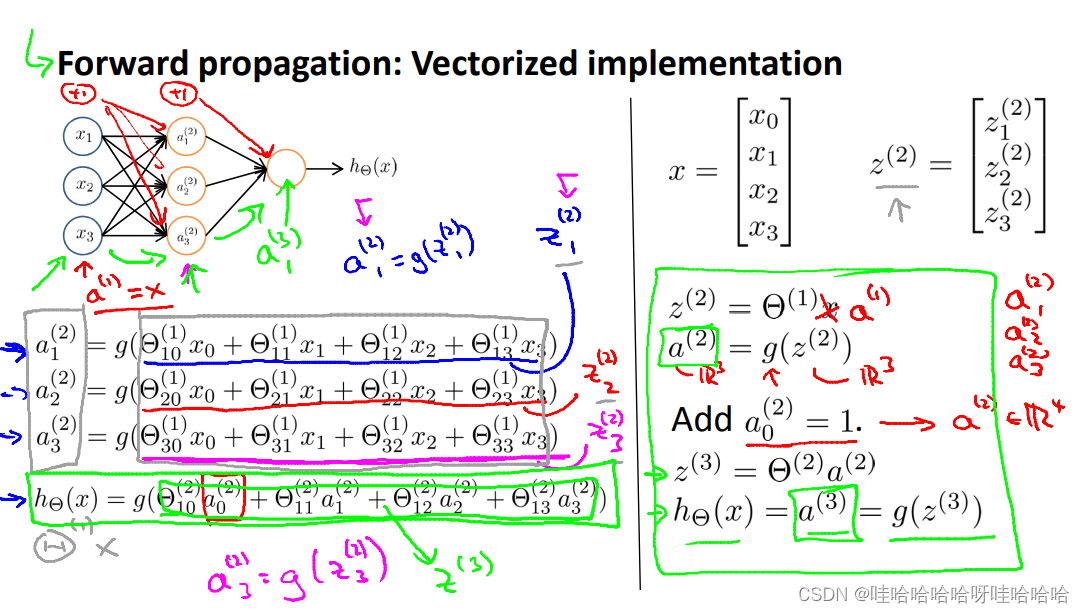
神经网络中神经元的连接方式称为神经网络架构(architecture)
架构指不同的神经元的连接方式。
hΘ(x)=a(3)=g(z(3))=g(Θ(2)a(2))=g(Θ(2)g(z(2)))=g(Θ(2)g(Θ(1)a(1)))h_Θ(x)=a^{(3)}=g(z^{(3)})=g(Θ^{(2)}a^{(2)})=g(Θ^{(2)}g(z^{(2)}))=g(Θ^{(2)}g(Θ^{(1)}a^{(1)}))hΘ(x)=a(3)=g(z(3))=g(Θ(2)a(2))=g(Θ(2)g(z(2)))=g(Θ(2)g(Θ(1)a(1)))
例子与直觉理解:Example and intuitions
神经网络实现逻辑与AND
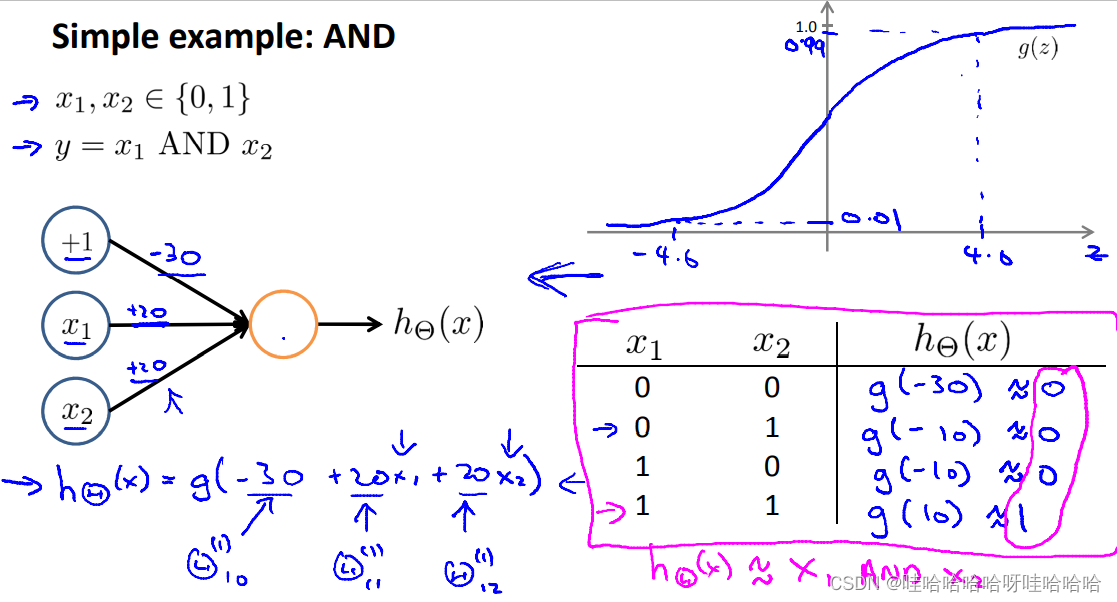 神经网络实现逻辑或OR
神经网络实现逻辑或OR
 神经网络实现逻辑或XNOR
神经网络实现逻辑或XNOR
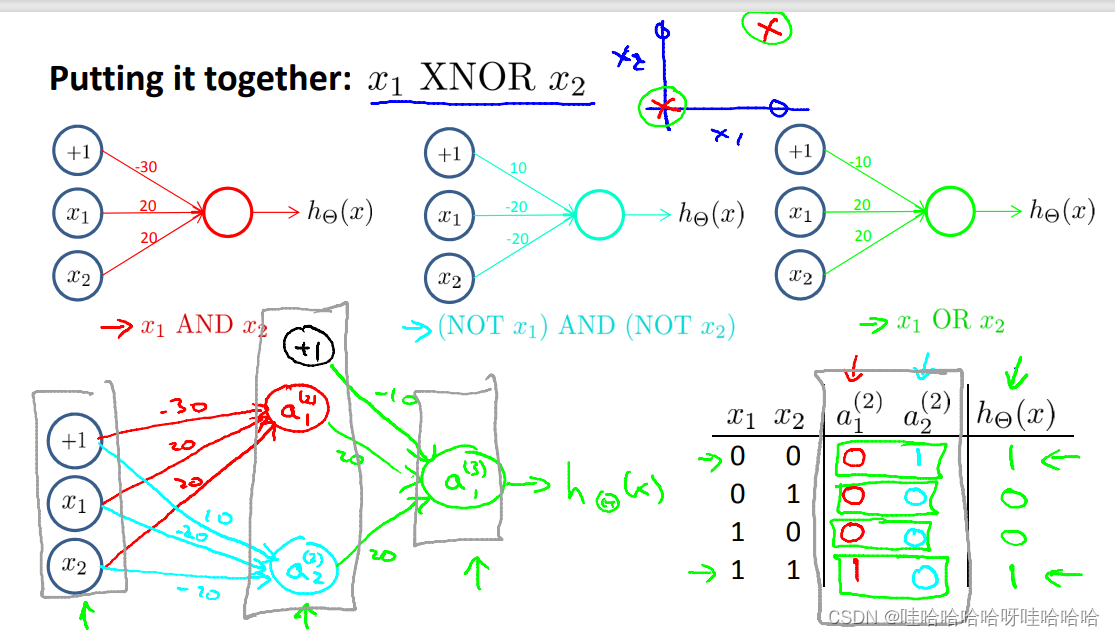
多类别分类:Mult-class classification
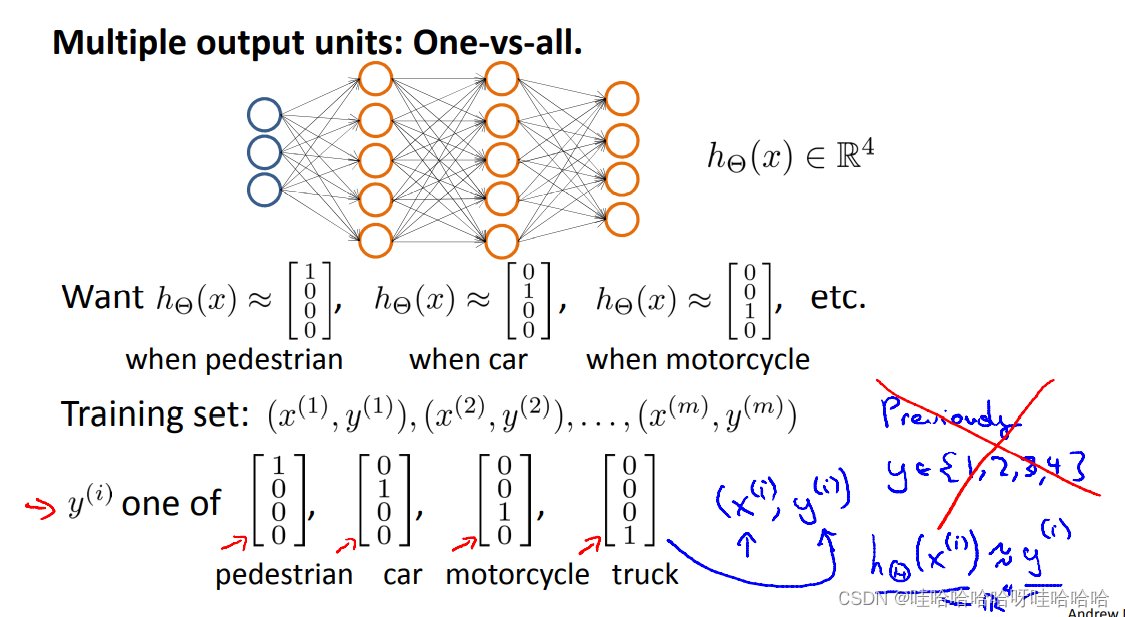




 这篇博客探讨了神经网络的基本构成,包括单个神经元的输入与输出,权重参数,以及Sigmoid激活函数的角色。它介绍了神经网络的三层结构——输入层、隐藏层和输出层,并通过前向传播解释了信息在神经元间的传递。此外,博客用实例说明了神经网络如何实现逻辑运算,如AND、OR和XNOR,进一步阐述了其在多类别分类中的应用。
这篇博客探讨了神经网络的基本构成,包括单个神经元的输入与输出,权重参数,以及Sigmoid激活函数的角色。它介绍了神经网络的三层结构——输入层、隐藏层和输出层,并通过前向传播解释了信息在神经元间的传递。此外,博客用实例说明了神经网络如何实现逻辑运算,如AND、OR和XNOR,进一步阐述了其在多类别分类中的应用。
















 471
471

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








