1.一维卡尔曼滤波(恒定的动态模型)
2.一维卡尔曼滤波(动态模型)
3.二维-卡尔曼滤波算法
1.使用场景
示例1:以一个6轴陀螺仪为例,它可以直接输出角度和加速度数据(2个测量数据),我们的目的是测量陀螺仪偏移的角度
直接输出的 角度 称之为测量值
同时我们也可以通过加速度经过一些计算,也会得到一个角度值,这个角度值称之为估计值
示例2:一辆做匀速行驶的小车(速度V=2m/s),上面有超声波测距,可以直接知道小车行驶的距离(2个测量数据)那么超声波测距在
Z
k
\displaystyle {{Z}_{k}}
Zk时刻输出的结果为测量值
我们也可以使用
S
k
=
V
⋅
t
k
\displaystyle {{S}_{k}}=V⋅{{t}_{k}}
Sk=V⋅tk或者
S
k
=
S
k
−
1
+
V
⋅
△
t
\displaystyle {{S}_{k}}={{S}_{k-1}}+V⋅△t
Sk=Sk−1+V⋅△t 求出行驶的距离估计值
从上面的两个例子知道,我们需要有两个参数测量值和估计值,这个估计值是我们通过一些别的手段获取到的,而卡尔曼滤波的作用就是结合测量值和估计值进行修正,得出一个最优的结果(一阶互补滤波也有这种效果)
如果是在一个连续变化的过程中,当前时刻的状态是由前一时刻的状态加上控制输入的影响(例如: S k = S k − 1 + V ⋅ △ t \displaystyle {{S}_{k}}={{S}_{k-1}}+V⋅△t Sk=Sk−1+V⋅△t),再加上一些不可预见的噪声(如环境干扰等)共同决定的。卡尔曼滤波器利用这些信息来预测系统在下一时刻的状态,并在此基础上进一步结合测量信息来修正这个预测。
如果测量的是1维的数据,只有一个测量值(例如:电压,电流,温湿度采集),应该使用2.一维卡尔曼滤波(动态模型)
2.流程图
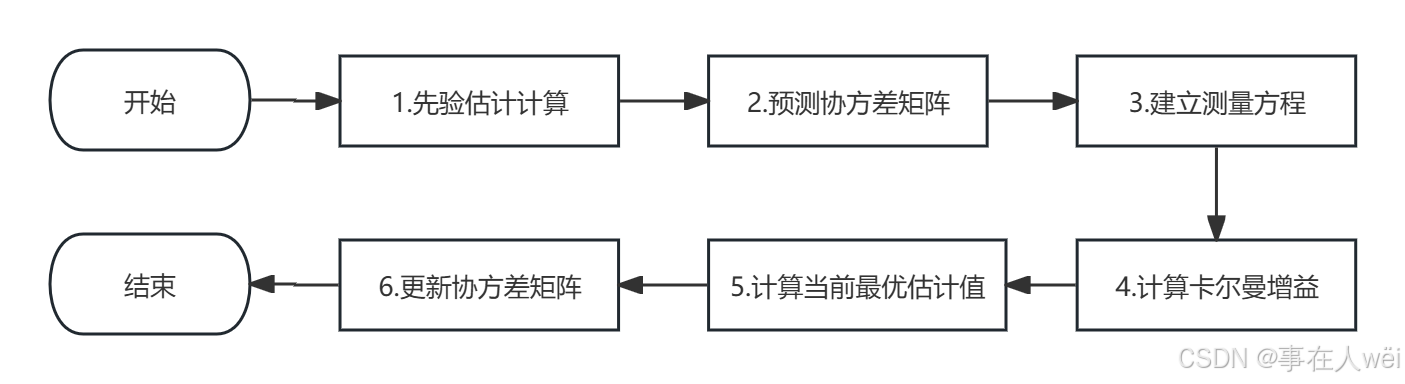
1. 先验估计计算
📌 固定公式 : X k = A ⋅ X k − 1 + B ⋅ U k + W k \displaystyle{{X}_{k}}=A⋅{{X}_{k-1}}+B⋅{{U}_{k}}+{{W}_{k}} Xk=A⋅Xk−1+B⋅Uk+Wk
- 状态向量 X k \displaystyle{{X}_{k}} Xk : 时刻 k的状态向量的先验估计,即在没有考虑时刻 k 测量信息的情况下的预测值。
-
X
\displaystyle{X}
X包含两个元素:
angle(角度)和Qbias(角速度的偏差估计)。这是我们需要估计的状态。
🧮 X = [ a n g l e Q b i a s ] \displaystyle X=\left [{\begin{matrix}angle\\Qbias\end{matrix}}\right ] X=[angleQbias]
a
n
g
l
e
\displaystyle angle
angle : 就是输出的最优结果
Q
b
i
a
s
\displaystyle Qbias
Qbias : 表示系统角速度的偏差估计,它用于校正新测量的角速度 newGyro,从而更准确地估计系统的角度。在每个dt时间步长内,角速度偏差 Qbias保持不变,但会在每次迭代中被用来校正测量值。这种做法有助于提高角度估计的准确性,尤其是在长时间运行过程中,累积误差可以通过不断更新 Qbias 来得到缓解。
- A \displaystyle {A} A : 系统矩阵 A 描述了系统状态随时间的自然演化。给定的系统矩阵为:
🧮 A = [ 1 − d t 0 1 ] \displaystyle A=\left [{\begin{matrix}1&-dt\\0&1\end{matrix}}\right ] A=[10−dt1]
dt为采样时间间隔。需要自定义好,该参数会影响到调教效果
static float dt = 0.01; // 代码01 采样周期即计算任务周期10ms
X k = A ⋅ X k − 1 \displaystyle {{X}_{k}}=A⋅{{X}_{k-1}} Xk=A⋅Xk−1含义说明:
🧮 [ θ k ω k ] = [ 1 − d t 0 1 ] ⋅ [ θ k − 1 ω k − 1 ] = [ θ k − 1 − d t ⋅ ω k − 1 ω k − 1 ] \displaystyle \left [{\begin{matrix}{{θ}_{k}}\\{{ω}_{k}}\end{matrix}}\right ]=\left [{\begin{matrix}1&-dt\\0&1\end{matrix}}\right ]⋅\left [{\begin{matrix}{{θ}_{k-1}}\\{{ω}_{k-1}}\end{matrix}}\right ]=\left [{\begin{matrix}{{θ}_{k-1}}-dt⋅{{ω}_{k-1}}\\{{ω}_{k-1}}\end{matrix}}\right ] [θkωk]=[10−dt1]⋅[θk−1ωk−1]=[θk−1−dt⋅ωk−1ωk−1]
θ k = θ k − 1 − d t ⋅ ω k − 1 \displaystyle {{θ}_{k}}={{θ}_{k-1}}-dt⋅{{ω}_{k-1}} θk=θk−1−dt⋅ωk−1 //新的角度 = 旧的角度 - 角速度 * 时间
ω k = ω k − 1 \displaystyle {{ω}_{k}}={{ω}_{k-1}} ωk=ωk−1 // 角速度在dt时间内保持不变
- B \displaystyle {B} B控制矩阵 B 描述了控制输入 Uk 对系统状态的影响。如果存在控制输入,则需要考虑 B⋅Uk项。如果没有控制输入,则 B 可以是零矩阵或者不包含该项。
🧮 B = [ d t 0 ] \displaystyle B=\left [{\begin{matrix}dt\\0\end{matrix}}\right ] B=[dt0]
-
U
k
\displaystyle {{U}_{k}}
Uk : 输入向量 U(k)表示在时刻 k影响系统的控制输入或其他外部因素。
例如,在导航系统中,这可以是加速度计读数或者是其他能够改变物体位置的信息。
🧮 U = [ u ] \displaystyle U=\left [{\begin{matrix}u\end{matrix}}\right ] U=[u] // u = newGyro陀螺仪测得的角速度
B ⋅ U k \displaystyle B⋅{{U}_{k}} B⋅Uk含义分析:
🧮 B ⋅ U k = [ d t 0 ] ⋅ [ u ] = [ d t ⋅ u 0 ] \displaystyle B⋅{{U}_{k}}=\left [{\begin{matrix}dt\\0\end{matrix}}\right ]⋅\left [{\begin{matrix}u\end{matrix}}\right ]=\left [{\begin{matrix}dt⋅u\\0\end{matrix}}\right ] B⋅Uk=[dt0]⋅[u]=[dt⋅u0]
第一行:对角度的影响:输入值u会导致角度发生变化,dt⋅u
第二行:对角速度的影响:输入值u不会直接影响到角速度
-
W
k
\displaystyle {{W}_{k}}
Wk
(忽略):过程噪声 W(k) 是一个随机变量,代表了未建模的动力学、外部干扰以及其他不确定因素。它反映了模型的不精确性和系统内部的随机变化。在实际应用中,W(k) 通常假设为零均值、高斯分布的白噪声。陀螺仪测得的角速度newGyro本身就带有了噪声,所以直接省略这个
总结:
📌 X k = A ⋅ X k − 1 + B ⋅ U k \displaystyle {{X}_{k}}=A⋅{{X}_{k-1}}+B⋅{{U}_{k}} Xk=A⋅Xk−1+B⋅Uk
[ a n g l e k Q b i a s k ] = [ 1 − d t 0 1 ] ⋅ [ a n g l e k − 1 Q b i a s k − 1 ] + [ d t 0 ] ⋅ n e w G y r o \displaystyle \left [{\begin{matrix}angl{{e}_{k}}\\Qbia{{s}_{k}}\end{matrix}}\right ]=\left [{\begin{matrix}1&-dt\\0&1\end{matrix}}\right ]⋅\left [{\begin{matrix}angl{{e}_{k-1}}\\Qbia{{s}_{k-1}}\end{matrix}}\right ]+\left [{\begin{matrix}dt\\0\end{matrix}}\right ]⋅newGyro [anglekQbiask]=[10−dt1]⋅[anglek−1Qbiask−1]+[dt0]⋅newGyro
= [ a n g l e k − 1 + ( − d t ) ⋅ Q b i a s k − 1 Q b i a s k − 1 ] + [ d t 0 ] ⋅ n e w G y r o \displaystyle =[\begin{matrix}angl{{e}_{k-1}}+(-dt)⋅Qbia{{s}_{k-1}}\\Qbia{{s}_{k-1}}\end{matrix}]+\left [{\begin{matrix}dt\\0\end{matrix}}\right ]⋅newGyro =[anglek−1+(−dt)⋅Qbiask−1Qbiask−1]+[dt0]⋅newGyro
= [ a n g l e k − 1 + ( − d t ) ⋅ Q b i a s k − 1 + d t ⋅ n e w G y r o Q b i a s k − 1 ] \displaystyle =[\begin{matrix}angl{{e}_{k-1}}+(-dt)⋅Qbia{{s}_{k-1}}+dt⋅newGyro\\Qbia{{s}_{k-1}}\end{matrix}] =[anglek−1+(−dt)⋅Qbiask−1+dt⋅newGyroQbiask−1]
[ a n g l e k Q b i a s k ] = [ a n g l e k − 1 + ( n e w G y r o − Q b i a s k − 1 ) ⋅ d t Q b i a s k − 1 ] \displaystyle \left [{\begin{matrix}angl{{e}_{k}}\\Qbia{{s}_{k}}\end{matrix}}\right ]=[\begin{matrix}angl{{e}_{k-1}}+(newGyro-Qbia{{s}_{k-1}})⋅dt\\Qbia{{s}_{k-1}}\end{matrix}] [anglekQbiask]=[anglek−1+(newGyro−Qbiask−1)⋅dtQbiask−1]
得到:(将下面部分使用代码来实现)
✅
a n g l e k = a n g l e k − 1 + ( n e w G y r o − Q b i a s k − 1 ) ⋅ d t \displaystyle angl{{e}_{k}}=angl{{e}_{k-1}}+(newGyro-Qbia{{s}_{k-1}})⋅dt anglek=anglek−1+(newGyro−Qbiask−1)⋅dt ---------------//代码1
Q b i a s k = Q b i a s k − 1 \displaystyle Qbia{{s}_{k}}=Qbia{{s}_{k-1}} Qbiask=Qbiask−1 ------------------------------------------------------------ //代码2(忽略)
( n e w G y r o − Q b i a s k − 1 ) \displaystyle (newGyro-Qbia{{s}_{k-1}}) (newGyro−Qbiask−1)表示修正后的角速度
2. 预测协方差矩阵
📌 固定公式 : P k = A ⋅ P k − 1 ⋅ A T + Q = P k − 1 + Q \displaystyle{{P}_{k}}=A⋅{{P}_{k-1}}⋅{{A}^{T}}+Q={{P}_{k-1}}+Q Pk=A⋅Pk−1⋅AT+Q=Pk−1+Q
- P k \displaystyle{{P}_{k}} Pk:这是时刻 k 的先验估计误差协方差矩阵。它描述了在没有考虑当前时刻 k 的测量信息时,状态向量 X k \displaystyle{{X}_{k}} Xk的估计不确定性。
🧮 P = [ P P 00 P P 01 P P 10 P P 11 ] \displaystyle P=\left [{\begin{matrix}P{{P}_{00}}&P{{P}_{01}}\\P{{P}_{10}}&P{{P}_{11}}\end{matrix}}\right ] P=[PP00PP10PP01PP11]
矩阵的性质
由于协方差矩阵是对称的,因此 P P 10 = P P 01 \displaystyle P{{P}_{10}}=P{{P}_{01}} PP10=PP01
这意味着矩阵可以写成:
P = [ P P 00 P P 01 P P 01 P P 11 ] \displaystyle P=\left [{\begin{matrix}P{{P}_{00}}&P{{P}_{01}}\\P{{P}_{01}}&P{{P}_{11}}\end{matrix}}\right ] P=[PP00PP01PP01PP11]初始值为 P = [ 1 0 0 1 ] \displaystyle P=\left [{\begin{matrix}1&0\\0&1\end{matrix}}\right ] P=[1001]
-
P P 00 \displaystyle PP00 PP00:表示角度 angle 的方差,即角度估计的不确定性。
-
P P 01 \displaystyle PP01 PP01 或 P P 10 \displaystyle PP10 PP10:表示状态向量第一个元素(角度 angle)和第二个元素(角速度偏差 Qbias)之间的协方差。如果协方差为正,表示两个变量倾向于同时增加或减少;如果协方差为负,则表示一个变量增加时另一个变量倾向于减少。
-
P P 11 \displaystyle PP11 PP11:表示角速度偏差 Qbias 的方差,即角速度偏差估计的不确定性。方差越大,表示对该状态的估计越不确定。
-
A \displaystyle A A:系统矩阵 A 描述了系统状态从一个时间步长到下一个时间步长之间的关系。
🧮 A = [ 1 − d t 0 1 ] \displaystyle A=\left [{\begin{matrix}1&-dt\\0&1\end{matrix}}\right ] A=[10−dt1]
- A T \displaystyle {{A}^{T}} AT:A 的转置矩阵。在矩阵乘法中, A \displaystyle {A} A和 A T \displaystyle {{A}^{T}} AT的组合用于传播不确定性。
🧮 A T = [ 1 0 − d t 1 ] \displaystyle {{A}^{T}}=\left [{\begin{matrix}1&0\\-dt&1\end{matrix}}\right ] AT=[1−dt01]
- Q \displaystyle {Q} Q:过程噪声协方差矩阵。角度和角速度的漂移噪声相互独立。
🧮 Q = [ Q a n g l e 0 0 Q g y r o ] \displaystyle Q=\left [{\begin{matrix}{{Q}_{angle}}&0\\0&{{Q}_{gyro}}\end{matrix}}\right ] Q=[Qangle00Qgyro]
Q a n g l e \displaystyle {{Q}_{angle}} Qangle和 Q g y r o \displaystyle {{Q}_{gyro}} Qgyro需要自定义好,这两个参数会影响到调教效果
static float Q_angle = 0.001; // 代码02 角度噪声的协方差
static float Q_gyro = 0.003; // 代码03 角速度噪声的协方差
总结:
📌 P k = A ⋅ P k − 1 ⋅ A T + Q \displaystyle {{P}_{k}}=A⋅{{P}_{k-1}}⋅{{A}^{T}}+Q Pk=A⋅Pk−1⋅AT+Q
[ P P 00 P P 01 P P 01 P P 11 ] = [ 1 − d t 0 1 ] ⋅ [ P P 00 k − 1 P P 01 k − 1 P P 01 k − 1 P P 11 k − 1 ] ⋅ [ 1 0 − d t 1 ] + [ Q a n g l e 0 0 Q g y r o ] \displaystyle\left [{\begin{matrix}P{{P}_{00}}&P{{P}_{01}}\\P{{P}_{01}}&P{{P}_{11}}\end{matrix}}\right ]=\left [{\begin{matrix}1&-dt\\0&1\end{matrix}}\right ]⋅\left [{\begin{matrix}P{{P}_{00k-1}}&P{{P}_{01k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ]⋅\left [{\begin{matrix}1&0\\-dt&1\end{matrix}}\right ]+\left [{\begin{matrix}{{Q}_{angle}}&0\\0&{{Q}_{gyro}}\end{matrix}}\right ] [PP00PP01PP01PP11]=[10−dt1]⋅[PP00k−1PP01k−1PP01k−1PP11k−1]⋅[1−dt01]+[Qangle00Qgyro]
- 先计算 A ⋅ P k − 1 \displaystyle A⋅{{P}_{k-1}} A⋅Pk−1部分
🧮 A ⋅ P k − 1 = [ 1 − d t 0 1 ] ⋅ [ P P 00 k − 1 P P 01 k − 1 P P 01 k − 1 P P 11 k − 1 ] \displaystyle A⋅{{P}_{k-1}} = \left [{\begin{matrix}1&-dt\\0&1\end{matrix}}\right ]⋅\left [{\begin{matrix}P{{P}_{00k-1}}&P{{P}_{01k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] A⋅Pk−1=[10−dt1]⋅[PP00k−1PP01k−1PP01k−1PP11k−1]
= [ P P 00 k − 1 − d t ⋅ P P 01 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 01 k − 1 P P 11 k − 1 ] \displaystyle =\left [{\begin{matrix}P{{P}_{00k-1}}-dt⋅P{{P}_{01k-1}}&P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] =[PP00k−1−dt⋅PP01k−1PP01k−1PP01k−1−dt⋅PP11k−1PP11k−1]
- 计算 A ⋅ P k − 1 ⋅ A T \displaystyle A⋅{{P}_{k-1}}⋅{{A}^{T}} A⋅Pk−1⋅AT部分
🧮
A ⋅ P k − 1 ⋅ A T = [ P P 00 k − 1 − d t ⋅ P P 01 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 01 k − 1 P P 11 k − 1 ] ⋅ [ 1 0 − d t 1 ] \displaystyle A⋅{{P}_{k-1}}⋅{{A}^{T}}=\left [{\begin{matrix}P{{P}_{00k-1}}-dt⋅P{{P}_{01k-1}}&P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ]⋅\left [{\begin{matrix}1&0\\-dt&1\end{matrix}}\right ] A⋅Pk−1⋅AT=[PP00k−1−dt⋅PP01k−1PP01k−1PP01k−1−dt⋅PP11k−1PP11k−1]⋅[1−dt01]
= [ ( P P 00 k − 1 − d t ⋅ P P 01 k − 1 ) − d t ⋅ ( P P 01 k − 1 − d t ⋅ P P 11 k − 1 ) P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 11 k − 1 ] \displaystyle =\left [{\begin{matrix}(P{{P}_{00k-1}}-dt⋅P{{P}_{01k-1}})-dt⋅(P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}})&P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}\\P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] =[(PP00k−1−dt⋅PP01k−1)−dt⋅(PP01k−1−dt⋅PP11k−1)PP01k−1−dt⋅PP11k−1PP01k−1−dt⋅PP11k−1PP11k−1]
= [ P P 00 k − 1 − 2 d t ⋅ P P 01 k − 1 + d t 2 ⋅ P P 11 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 11 k − 1 ] \displaystyle =\left [{\begin{matrix}P{{P}_{00k-1}}-2dt⋅P{{P}_{01k-1}}+d{{t}^{2}}⋅P{{P}_{11k-1}}&P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}\\P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] =[PP00k−1−2dt⋅PP01k−1+dt2⋅PP11k−1PP01k−1−dt⋅PP11k−1PP01k−1−dt⋅PP11k−1PP11k−1]
- 简化计算
由于 d t 2 \displaystyle d{{t}^{2}} dt2较小,可以忽略。因此,进一步简化上面的结果:
🧮 A ⋅ P k − 1 ⋅ A T = [ P P 00 k − 1 − 2 d t ⋅ P P 01 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 11 k − 1 ] \displaystyle A⋅{{P}_{k-1}}⋅{{A}^{T}}=\left [{\begin{matrix}P{{P}_{00k-1}}-2dt⋅P{{P}_{01k-1}}&P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}\\P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] A⋅Pk−1⋅AT=[PP00k−1−2dt⋅PP01k−1PP01k−1−dt⋅PP11k−1PP01k−1−dt⋅PP11k−1PP11k−1]
- 计算 A ⋅ P k − 1 ⋅ A T + Q \displaystyle A⋅{{P}_{k-1}}⋅{{A}^{T}}+Q A⋅Pk−1⋅AT+Q部分
🧮
A ⋅ P k − 1 ⋅ A T + Q = [ P P 00 k − 1 − 2 d t ⋅ P P 01 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 01 k − 1 − d t ⋅ P P 11 k − 1 P P 11 k − 1 ] + [ Q a n g l e 0 0 Q g y r o ] \displaystyle A⋅{{P}_{k-1}}⋅{{A}^{T}}+Q=\left [{\begin{matrix}P{{P}_{00k-1}}-2dt⋅P{{P}_{01k-1}}&P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}\\P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ]+\left [{\begin{matrix}{{Q}_{angle}}&0\\0&{{Q}_{gyro}}\end{matrix}}\right ] A⋅Pk−1⋅AT+Q=[PP00k−1−2dt⋅PP01k−1PP01k−1−dt⋅PP11k−1PP01k−1−dt⋅PP11k−1PP11k−1]+[Qangle00Qgyro]
得到:(将下面部分使用代码来实现)
✅
P P 00 = P P 00 k − 1 − 2 d t ⋅ P P 01 k − 1 + Q a n g l e \displaystyle P{{P}_{00}}=P{{P}_{00k-1}}-2dt⋅P{{P}_{01k-1}}+{{Q}_{angle}} PP00=PP00k−1−2dt⋅PP01k−1+Qangle -------------------//代码3
P P 01 = P P 10 = P P 01 k − 1 − d t ⋅ P P 11 k − 1 \displaystyle P{{P}_{01}}=P{{P}_{10}}=P{{P}_{01k-1}}-dt⋅P{{P}_{11k-1}} PP01=PP10=PP01k−1−dt⋅PP11k−1 ---------------------//代码4
P P 11 = P P 11 k − 1 + Q g y r o \displaystyle P{{P}_{11}}=P{{P}_{11k-1}}+{{Q}_{gyro}} PP11=PP11k−1+Qgyro ---------------------------------------------//代码5
3. 建立测量方程
下面是理论,可以忽略,直接看结果
📌 固定公式 : Z k = H X k + V k \displaystyle {{Z}_{k}}=H{{X}_{k}}+{{V}_{k}} Zk=HXk+Vk
- H \displaystyle {H} H : 测量矩阵
🧮 H = [ 1 0 ] \displaystyle H=\left [{\begin{matrix}1&0\end{matrix}}\right ] H=[10]
这意味着测量值 Z k \displaystyle {{Z}_{k}} Zk只与状态向量的第一个元素 angle 相关,与第二个元素 Qbias 无关
🧮 Z k = H X k + V k \displaystyle {{Z}_{k}}=H{{X}_{k}}+{{V}_{k}} Zk=HXk+Vk
= [ 1 0 ] ⋅ [ a n g l e Q b i a s ] + V k \displaystyle= \left [{\begin{matrix}1&0\end{matrix}}\right ]⋅\left [{\begin{matrix}angle\\Qbias\end{matrix}}\right ]+{{V}_{k}} =[10]⋅[angleQbias]+Vk
= a n g l e + V k \displaystyle = angle+{{V}_{k}} =angle+Vk
测量值
Z
k
\displaystyle {{Z}_{k}}
Zk实际上是系统真实状态加上测量噪声
V
k
\displaystyle{{V}_{k}}
Vk ,
在实际中,我们获取到的传感器参数
n
e
w
A
n
g
l
e
\displaystyle newAngle
newAngle 本身就自带了噪声,所以
V
k
\displaystyle{{V}_{k}}
Vk 可以省略
得到:(将下面部分使用代码来实现)
✅ Z k = n e w A n g l e \displaystyle {{Z}_{k}}=newAngle Zk=newAngle (传感器获取到的数据)--------------------------//代码6
4. 计算卡尔曼增益
📌 固定公式 : K g ( k ) = P k − 1 ⋅ H T H P k − 1 ⋅ H T + R a n g l e \displaystyle {{K}_{g(k)}}=\frac{{{P}_{k-1}}⋅{{H}^{T}}}{H{{P}_{k-1}}⋅{{H}^{T}}+{{R}_{angle}}} Kg(k)=HPk−1⋅HT+RanglePk−1⋅HT
- P k − 1 \displaystyle {{P}_{k-1}} Pk−1 是预测的误差协方差矩阵,
- H \displaystyle {H} H 是测量矩阵,
- R a n g l e \displaystyle {{R}_{angle}} Rangle 是测量噪声的协方差矩阵,需要自定义好
static float R_angle = 0.5; // 代码04 加速度计测量噪声的协方差
- 先计算 P k − 1 ⋅ H T \displaystyle {{P}_{k-1}}⋅{{H}^{T}} Pk−1⋅HT部分
🧮 P k − 1 ⋅ H T = [ P P 00 k − 1 P P 01 k − 1 P P 01 k − 1 P P 11 k − 1 ] ⋅ [ 1 0 ] = [ P P 00 k − 1 P P 01 k − 1 ] \displaystyle {{P}_{k-1}}⋅{{H}^{T}}=\left [{\begin{matrix}P{{P}_{00k-1}}&P{{P}_{01k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ]⋅\left [{\begin{matrix}1\\0\end{matrix}}\right ] = \left [{\begin{matrix}P{{P}_{00k-1}}\\P{{P}_{01k-1}}\end{matrix}}\right ] Pk−1⋅HT=[PP00k−1PP01k−1PP01k−1PP11k−1]⋅[10]=[PP00k−1PP01k−1]
- 计算 H P k − 1 ⋅ H T \displaystyle H{{P}_{k-1}}⋅{{H}^{T}} HPk−1⋅HT部分
🧮 H P k − 1 ⋅ H T = [ 1 0 ] ⋅ [ P P 00 k − 1 P P 01 k − 1 P P 01 k − 1 P P 11 k − 1 ] ⋅ [ 1 0 ] \displaystyle H{{P}_{k-1}}⋅{{H}^{T}}=\left [{\begin{matrix}1&0\end{matrix}}\right ]⋅\left [{\begin{matrix}P{{P}_{00k-1}}&P{{P}_{01k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ]⋅\left [{\begin{matrix}1\\0\end{matrix}}\right ] HPk−1⋅HT=[10]⋅[PP00k−1PP01k−1PP01k−1PP11k−1]⋅[10]
= [ 1 0 ] ⋅ [ P P 00 k − 1 P P 01 k − 1 ] \displaystyle =\left [{\begin{matrix}1&0\end{matrix}}\right ]⋅\left [{\begin{matrix}P{{P}_{00k-1}}\\P{{P}_{01k-1}}\end{matrix}}\right ] =[10]⋅[PP00k−1PP01k−1]
= P P 00 k − 1 \displaystyle =P{{P}_{00k-1}} =PP00k−1
H P k − 1 ⋅ H T + R a n g l e = P P 00 k − 1 + R a n g l e \displaystyle H{{P}_{k-1}}⋅{{H}^{T}}+{{R}_{angle}}=P{{P}_{00k-1}}+{{R}_{angle}} HPk−1⋅HT+Rangle=PP00k−1+Rangle
✅ K g ( k ) = P k − 1 ⋅ H T H P k − 1 ⋅ H T + R a n g l e = [ P P 00 k − 1 P P 00 k − 1 + R a n g l e P P 01 k − 1 P P 00 k − 1 + R a n g l e ] \displaystyle {{K}_{g(k)}}=\frac{{{P}_{k-1}}⋅{{H}^{T}}}{H{{P}_{k-1}}⋅{{H}^{T}}+{{R}_{angle}}}=\left [{\begin{matrix}\frac{P{{P}_{00k-1}}}{P{{P}_{00k-1}}+{{R}_{angle}}}\\\frac{P{{P}_{01k-1}}}{P{{P}_{00k-1}}+{{R}_{angle}}}\end{matrix}}\right ] Kg(k)=HPk−1⋅HT+RanglePk−1⋅HT=[PP00k−1+RanglePP00k−1PP00k−1+RanglePP01k−1]
K 0 = P P 00 k − 1 P P 00 k − 1 + R a n g l e \displaystyle {{K}_{0}}=\frac{P{{P}_{00k-1}}}{P{{P}_{00k-1}}+{{R}_{angle}}} K0=PP00k−1+RanglePP00k−1 (角度偏差的卡尔曼增益) ----------------//代码7
K 1 = P P 01 k − 1 P P 00 k − 1 + R a n g l e \displaystyle {{K}_{1}}=\frac{P{{P}_{01k-1}}}{P{{P}_{00k-1}}+{{R}_{angle}}} K1=PP00k−1+RanglePP01k−1 (角速度偏差的卡尔曼增益) -------------//代码8
这些增益将用于后续的状态更新步骤,以融合测量信息和预测信息来改进状态估计。
5.计算当前最优估计值
📌 固定公式 : X k = X k − 1 + K g ( k ) ⋅ ( Z k − H ⋅ X k − 1 ) \displaystyle {{X}_{k}}={{X}_{k-1}}+{{K}_{g(k)}}⋅({{Z}_{k}}-H⋅{{X}_{k-1}}) Xk=Xk−1+Kg(k)⋅(Zk−H⋅Xk−1)
[ a n g l e k Q b i a s k ] = [ a n g l e k − 1 Q b i a s k − 1 ] + [ K 0 K 1 ] ⋅ ( Z k − [ 1 0 ] ⋅ [ a n g l e k − 1 Q b i a s k − 1 ] ) \displaystyle \left [{\begin{matrix}angl{{e}_{k}}\\Qbia{{s}_{k}}\end{matrix}}\right ]=\left [{\begin{matrix}angl{{e}_{k-1}}\\Qbia{{s}_{k-1}}\end{matrix}}\right ]+\left [{\begin{matrix}{{K}_{0}}\\{{K}_{1}}\end{matrix}}\right ]⋅({{Z}_{k}}-\left [{\begin{matrix}1&0\end{matrix}}\right ]⋅\left [{\begin{matrix}angl{{e}_{k-1}}\\Qbia{{s}_{k-1}}\end{matrix}}\right ]) [anglekQbiask]=[anglek−1Qbiask−1]+[K0K1]⋅(Zk−[10]⋅[anglek−1Qbiask−1])
= [ a n g l e k − 1 Q b i a s k − 1 ] + [ K 0 K 1 ] ⋅ ( Z k − a n g l e k − 1 ) \displaystyle =\left [{\begin{matrix}angl{{e}_{k-1}}\\Qbia{{s}_{k-1}}\end{matrix}}\right ]+\left [{\begin{matrix}{{K}_{0}}\\{{K}_{1}}\end{matrix}}\right ]⋅({{Z}_{k}}-angl{{e}_{k-1}}) =[anglek−1Qbiask−1]+[K0K1]⋅(Zk−anglek−1)
✅
a n g l e k = a n g l e k − 1 + K 0 ⋅ ( Z k − a n g l e k − 1 ) \displaystyle angl{{e}_{k}}=angl{{e}_{k-1}}+{{K}_{0}}⋅({{Z}_{k}}-angl{{e}_{k-1}}) anglek=anglek−1+K0⋅(Zk−anglek−1) ---------------//代码9
Q b i a k = Q b i a k − 1 + K 1 ⋅ ( Z k − a n g l e k − 1 ) \displaystyle Qbi{{a}_{k}}=Qbi{{a}_{k-1}}+{{K}_{1}}⋅({{Z}_{k}}-angl{{e}_{k-1}}) Qbiak=Qbiak−1+K1⋅(Zk−anglek−1) -----------------//代码10
输出的 a n g l e k \displaystyle angl{{e}_{k}} anglek就是卡尔曼滤波后的最优估计值
6.更新协方差矩阵
📌 固定公式 : P k = [ I − K g ( k ) ⋅ H ] ⋅ P k − 1 \displaystyle {{P}_{k}}=\left [{\begin{matrix}I-{{K}_{g(k)}}⋅H\end{matrix}}\right ]⋅{{P}_{k-1}} Pk=[I−Kg(k)⋅H]⋅Pk−1
I \displaystyle I I:单位矩阵 [ 1 0 0 1 ] \displaystyle \left [{\begin{matrix}1&0\\0&1\end{matrix}}\right ] [1001]
🧮 P k = [ I − K g ( k ) ⋅ H ] ⋅ P k − 1 \displaystyle {{P}_{k}}=\left [{\begin{matrix}I-{{K}_{g(k)}}⋅H\end{matrix}}\right ]⋅{{P}_{k-1}} Pk=[I−Kg(k)⋅H]⋅Pk−1
[ P P 00 k P P 01 k P P 01 k P P 11 k ] = [ [ 1 0 0 1 ] − [ K 0 K 1 ] ⋅ [ 1 0 ] ] ⋅ [ P P 00 k − 1 P P 01 k − 1 P P 01 k − 1 P P 11 k − 1 ] \displaystyle \left [{\begin{matrix}P{{P}_{00k}}&P{{P}_{01k}}\\P{{P}_{01k}}&P{{P}_{11k}}\end{matrix}}\right ]=\left [{\begin{matrix}\left [{\begin{matrix}1&0\\0&1\end{matrix}}\right ]-\left [{\begin{matrix}{{K}_{0}}\\{{K}_{1}}\end{matrix}}\right ]⋅\left [{\begin{matrix}1&0\end{matrix}}\right ]\end{matrix}}\right ]⋅\left [{\begin{matrix}P{{P}_{00k-1}}&P{{P}_{01k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] [PP00kPP01kPP01kPP11k]=[[1001]−[K0K1]⋅[10]]⋅[PP00k−1PP01k−1PP01k−1PP11k−1]
[ P P 00 k P P 01 k P P 01 k P P 11 k ] = [ [ 1 0 0 1 ] − [ K 0 0 K 1 0 ] ] ⋅ [ P P 00 k − 1 P P 01 k − 1 P P 01 k − 1 P P 11 k − 1 ] \displaystyle \left [{\begin{matrix}P{{P}_{00k}}&P{{P}_{01k}}\\P{{P}_{01k}}&P{{P}_{11k}}\end{matrix}}\right ]=\left [{\begin{matrix}\left [{\begin{matrix}1&0\\0&1\end{matrix}}\right ]-\left [{\begin{matrix}{{K}_{0}}&0\\{{K}_{1}}&0\end{matrix}}\right ]\end{matrix}}\right ]⋅\left [{\begin{matrix}P{{P}_{00k-1}}&P{{P}_{01k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] [PP00kPP01kPP01kPP11k]=[[1001]−[K0K100]]⋅[PP00k−1PP01k−1PP01k−1PP11k−1]
[ P P 00 k P P 01 k P P 01 k P P 11 k ] = [ 1 − K 0 0 − K 1 1 ] ⋅ [ P P 00 k − 1 P P 01 k − 1 P P 01 k − 1 P P 11 k − 1 ] \displaystyle \left [{\begin{matrix}P{{P}_{00k}}&P{{P}_{01k}}\\P{{P}_{01k}}&P{{P}_{11k}}\end{matrix}}\right ]=\left [{\begin{matrix}1-{{K}_{0}}&0\\-{{K}_{1}}&1\end{matrix}}\right ]⋅\left [{\begin{matrix}P{{P}_{00k-1}}&P{{P}_{01k-1}}\\P{{P}_{01k-1}}&P{{P}_{11k-1}}\end{matrix}}\right ] [PP00kPP01kPP01kPP11k]=[1−K0−K101]⋅[PP00k−1PP01k−1PP01k−1PP11k−1]
[ P P 00 k P P 01 k P P 01 k P P 11 k ] = [ ( 1 − K 0 ) ⋅ P P 00 k − 1 ( 1 − K 0 ) ⋅ P P 01 k − 1 P P 01 k − 1 − K 1 ⋅ P P 00 k − 1 − K 1 ⋅ P P 01 k − 1 + P P 11 k − 1 ] \displaystyle \left [{\begin{matrix}P{{P}_{00k}}&P{{P}_{01k}}\\P{{P}_{01k}}&P{{P}_{11k}}\end{matrix}}\right ]=\left [{\begin{matrix}(1-{{K}_{0}})⋅P{{P}_{00k-1}}&(1-{{K}_{0}})⋅P{{P}_{01k-1}}\\P{{P}_{01k-1}}-{{K}_{1}}⋅P{{P}_{00k-1}}&-{{K}_{1}}⋅P{{P}_{01k-1}}+P{{P}_{11k-1}}\end{matrix}}\right ] [PP00kPP01kPP01kPP11k]=[(1−K0)⋅PP00k−1PP01k−1−K1⋅PP00k−1(1−K0)⋅PP01k−1−K1⋅PP01k−1+PP11k−1]
✅
P P 00 = ( 1 − K 0 ) ⋅ P P 00 k − 1 \displaystyle P{{P}_{00}}=(1-{{K}_{0}})⋅P{{P}_{00k-1}} PP00=(1−K0)⋅PP00k−1 ------------------------//代码11
P P 01 = ( 1 − K 0 ) ⋅ P P 01 k − 1 \displaystyle P{{P}_{01}}=(1-{{K}_{0}})⋅P{{P}_{01k-1}} PP01=(1−K0)⋅PP01k−1 ------------------------//代码12
P P 10 = P P 01 k − 1 − K 1 ⋅ P P 00 k − 1 \displaystyle P{{P}_{10}}=P{{P}_{01k-1}}-{{K}_{1}}⋅P{{P}_{00k-1}} PP10=PP01k−1−K1⋅PP00k−1 ---------------//代码13 (PP10 = PP01)
P P 11 = − K 1 ⋅ P P 01 k − 1 + P P 11 k − 1 \displaystyle P{{P}_{11}}=-{{K}_{1}}⋅P{{P}_{01k-1}}+P{{P}_{11k-1}} PP11=−K1⋅PP01k−1+PP11k−1 ------------//代码14
前面说过,由于协方差矩阵是对称的,因此
P
P
10
=
P
P
01
\displaystyle P{{P}_{10}}=P{{P}_{01}}
PP10=PP01
把数代进去验证,可以发现
(
1
−
K
0
)
⋅
P
P
01
k
−
1
\displaystyle (1-{{K}_{0}})⋅P{{P}_{01k-1}}
(1−K0)⋅PP01k−1 和
P
P
01
k
−
1
−
K
1
⋅
P
P
00
k
−
1
\displaystyle P{{P}_{01k-1}}-{{K}_{1}}⋅P{{P}_{00k-1}}
PP01k−1−K1⋅PP00k−1确实是相等的
7.实现代码
// 卡尔曼参数
static float dt = 0.01; // 代码01 采样周期即计算任务周期10ms
static float Q_angle = 0.001; // 代码02 角度噪声的协方差
static float Q_gyro = 0.003; // 代码03 角速度噪声的协方差
static float R_angle = 0.5; // 代码04 加速度计测量噪声的协方差
float angle_k; // 滤波后数据
void Kalman_Cal_Roll(float newAngle, float newGyro)
{
static float Q_bias; // Q_bias:陀螺仪的偏差 Angle_err:角度偏量
static float K_0, K_1; // 卡尔曼增益 K_0:用于计算最优估计值 K_1:用于计算最优估计值的偏差 t_0/1:中间变量
static float PP[2][2] = {{1, 0}, {0, 1}}; // 过程协方差矩阵P,初始值为单位阵
float Z_k;
// 1.先验估计计算
angle_k = angle_k + (newGyro - Q_bias) * dt; // 代码1 状态方程,角度值等于上次最优角度加角速度减零漂后积分
// 2.预测协方差矩阵
PP[0][0] = PP[0][0] - 2 * PP[0][1] * dt + Q_angle; // 代码3
PP[0][1] = PP[0][1] - PP[1][1] * dt; // 代码4
PP[1][0] = PP[0][1]; // 代码4
PP[1][1] = PP[1][1] + Q_gyro; // 代码5
// 3.建立测量方程
Z_k = newAngle; // 代码6
// 4.计算卡尔曼增益
K_0 = PP[0][0] / (PP[0][0] + R_angle); // 代码7
K_1 = PP[0][1] / (PP[0][0] + R_angle); // 代码8
// 5.计算当前最优估计值
angle_k = angle_k + K_0 * (Z_k - angle_k); // 代码9
Q_bias = Q_bias + K_1 * (Z_k - angle_k); // 代码10
// 6.更新协方差矩阵
PP[0][0] = PP[0][0] - K_0 * PP[0][0]; // 代码11
PP[0][1] = PP[0][1] - K_0 * PP[0][1]; // 代码12
PP[1][0] = PP[0][1]; // 代码13
PP[1][1] = PP[1][1] - K_1 * PP[0][1]; // 代码14
}
卡尔曼滤波需要我们来调教,分别调节下面的参数,会获取到不同的滤波效果
static float dt = 0.01; // 代码01 采样周期即计算任务周期10ms
static float Q_angle = 0.001; // 代码02 角度噪声的协方差
static float Q_gyro = 0.003; // 代码03 角速度噪声的协方差
static float R_angle = 0.5; // 代码04 加速度计测量噪声的协方差





















 3704
3704

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








