线性回归算法（涉及最小二乘法、梯度下降法）

目录：
一、简单线性回归算法
二、向量化
三、衡量线性回归法的指标MSE、RMS、MAE、R Squared 指标
四，多元线性回归（最小二乘法）
五、多元线性回归（梯度下降法）

一、简单线性回归算法
1、优点：
（1）解决回归问题
（2）思想简单，实现容易
（3）许多强大的非线性模型的基础
（4）结果具有很好的可解释性
（5）蕴含机器学习中的很多重要思想

2、什么是线性回归
（1）寻找一条直线，最大程度地拟合样本特征和样本输出标记之间的关系
（2）样本特征只有一个称为简单线性回归
（3）样本特征有多个称为多元线性回归

3、目标
（1）真值：

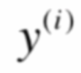
（2）预测值：

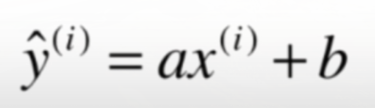
（3）目标：

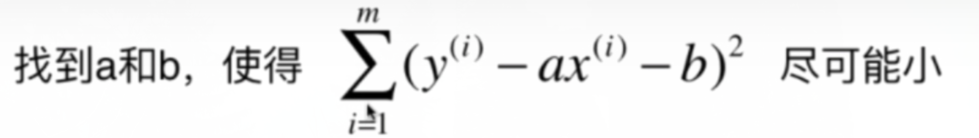
4、机器学习算法的基本思路
（1）损失函数：度量样本没有拟合的程度

（2）效用函数：度量拟合的程度
（3）通过分析问题，确定问题的损失函数或效用函数；通过最优化损失函数或者效用函数，获得机器学习模型，近乎所有参数学习算法都是这样的套路，如线性回归，SVM，多项式回归，神经网络，逻辑回归…

5、通过最小二乘法计算a,b的值
（1）

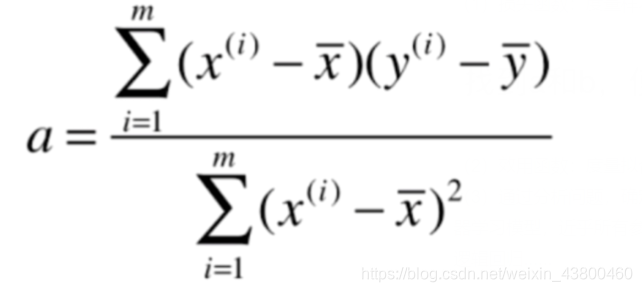
（2）

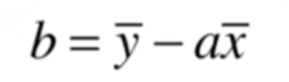
6、创建SimpleLinearRegression类

import numpy as np
import matplotlib.pyplot as plt

#定义一个类，注意括号是空的，因为我们要从空白创建这个类
class SimpleLinearRegression1():
     def _init_(self):
         #初始化属性a,b。a,b用于储存计算生成的结果，不是用户输入数据
         self.a_=None
         self.b_=None
         
         #fit方法，x_train,y_train是用户输入数据
     def fit(self,x_train,y_train):
         #根据训练数据集x_train,y_train训练线性回归模型
         assert x_train.ndim==1,\
             "Simple Linear Regressor can only solve single feature training data."
         assert len(x_train)==len(y_train),\
             "the size of x_train must be equal to the size of y_train"
            
            #计算x,y平均值
         x_mean=np.mean(x_train)
         y_mean=np.mean(y_train)
        
        #计算a,b的值
         num=0.0
         d=0.0
         for x,y in zip(x_train,y_train):
             num+=(x-x_mean)*(y-y_mean)
             d+=(x-x_mean)**2
         self.a_=num/d
         self.b_=y_mean-self.a_*x_mean
        
         return self
    
     #predict方法
     def predict(self,x_predict):
         #给定待测数据集x_predict，返回表示x_predict的结果向量
         assert x_predict.ndim==1,\
             "Simple Linear Regressor can only solve single feature training data."
         assert self.a_ is not None and self.b_ is not None,\
             "must fit before predict!"
            
         return np.array([self._predict(x) for x in x_predict])
     
     #_predict方法
     def _predict(self,x_single):
         #给定待测数据集x_single，返回表示x_single的预测结果值
         return self.a_*x_single+self.b_
    
     #_repr_方法，字符串输出
     def _repr_(self):
         return"SimpleLinearRegression1()"

7、根据SimpleLinearRegression类创建一个实例

import numpy as np
import matplotlib.pyplot as plt
from SimpleLinearRegression import SimpleLinearRegression1


x=np.array([1,2,3,4,5])
y=np.array([1,3,2,3,5])

#创建一个实例
reg1