机器学习（线性回归）

原创于 2025-10-27 15:42:33 发布 · 879 阅读

25 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #线性回归 #人工智能

1. 什么是线性回归？

核心思想：线性回归是一种通过拟合自变量（特征）与因变量（标签）之间的线性关系来进行预测的监督学习算法。

通俗解释：我们认为要预测的目标（比如房价）和其特征（比如面积、位置）之间存在一种“直线”关系。我们的目标是找到一条“最佳”的直线（或平面/超平面），使得这条直线能够尽可能准确地根据特征来预测目标。

主要类型：

简单线性回归：只有一个自变量。Y = wX + b
多元线性回归：有多个自变量。Y = w₁X₁ + w₂X₂ + ... + wₙXₙ + b

其中：

Y：我们要预测的因变量或目标值。
X, X₁, X₂, ... Xₙ：用于预测的自变量或特征。
w, w₁, w₂, ... wₙ：模型的权重或系数，表示每个特征对预测结果的重要性。
b：偏置项或截距，表示当所有特征都为0时，预测值的基准。

2. 模型表示

对于一个有 n 个特征的样本，线性回归模型的假设函数为：

y^=w1x1+w2x2+...+wnxn+by^=w1x1+w2x2+...+wnxn+b

为了公式的简洁和计算方便，我们通常会引入一个虚拟特征 x0=1x0=1，这样可以将偏置项 b 合并到权重向量中。模型可以改写为向量化的形式：

y^=WT⋅Xy^=WT⋅X

其中：

W=[w0,w1,w2,...,wn]W=[w0,w1,w2,...,wn] 是权重向量（这里 w0=bw0=b）。
X=[1,x1,x2,...,xn]X=[1,x1,x2,...,xn] 是特征向量。

y^y^ 是模型对样本 XX 的预测值。

3. 损失函数 - 如何衡量“最佳”？

我们需要一个标准来判断哪条直线是“最佳”的。这个标准就是损失函数。在线性回归中，最常用的损失函数是均方误差。

均方误差：所有样本的预测值与真实值之差的平方和的平均值。

J(W)=12m∑i=1m(y^(i)−y(i))2J(W)=2m1i=1∑m(y^(i)−y(i))2

其中：

mm：训练集中样本的数量。
y^(i)y^(i)：模型对第 ii 个样本的预测值。
y(i)y(i)：第 ii 个样本的真实值。
乘以 1221 是为了后续求导计算方便，不影响最终结果。

我们的目标：找到一组权重 WW，使得损失函数 J(W)J(W) 的值最小。

4. 参数学习 - 如何找到“最佳”参数？

有两种主要方法来最小化损失函数，找到最优的 WW。

方法一：梯度下降法

这是一种迭代优化算法，是机器学习中最常用的参数学习方法。

思想：想象你站在一座山上，想要以最快的速度下到山谷。你会环顾四周，找到最陡峭的方向向下走一步，然后重复这个过程，直到到达谷底。

数学实现：

随机初始化权重 WW。
重复直到收敛（损失函数的变化非常小）：
- 计算损失函数 J(W)J(W) 对每个权重 wjwj 的偏导数（即梯度）。
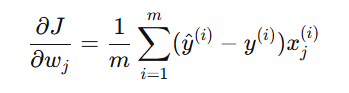
- 同时更新所有权重：
  
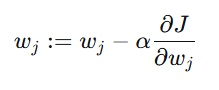
  其中 α 是学习率，控制每次更新的步长。

学习率的重要性：

太小：收敛速度慢，需要很多次迭代。
太大：可能无法收敛，甚至发散（越过最低点）。

方法二：正规方程法

这是一种基于解析解的数学方法，可以直接通过公式计算出最优的 W。

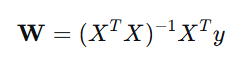
其中：

X是一个 m×(n+1)的矩阵，每一行是一个样本的特征向量（包含 x0=1）。
y 是一个包含所有 m 个样本真实值的向量。

两种方法对比：

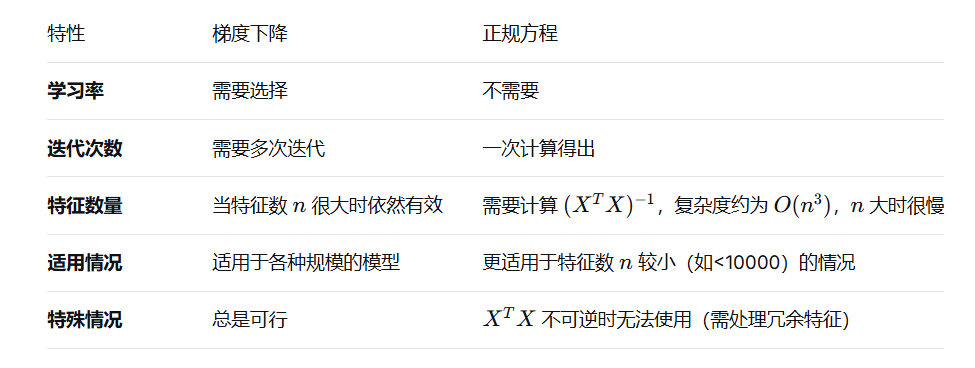
5. 模型评估

在模型训练完成后，我们需要评估它的性能。常用的指标有：

均方误差：与损失函数相同，直接反映预测误差的平方水平。
均方根误差：对MSE开方，使其量纲与目标变量 y 一致，更易于解释。
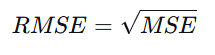
平均绝对误差：预测值与真实值之差的绝对值的平均值，对异常值不如MSE敏感。
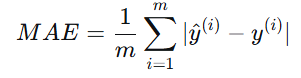
R平方：表示模型能够解释的目标变量方差的比例。取值范围通常在0到1之间，越接近1说明模型拟合得越好。

6. 假设与局限性

线性回归并非万能，它基于一些重要的假设：

线性关系：假设特征与目标之间存在线性关系。
误差独立性：误差项之间相互独立。
同方差性：误差项的方差应为常数。
误差正态分布：误差项应服从均值为0的正态分布。
多重共线性：特征之间不应存在高度相关性，否则会影响权重估计的稳定性和可解释性。

如果这些假设被严重违反，线性回归模型的性能可能会大打折扣。

7. 实践中的技巧与处理

特征缩放：在使用梯度下降法时，如果特征尺度差异很大，应先进行归一化或标准化，以加速收敛。
多项式回归：如果关系是非线性的，可以通过添加特征的高次项（如 x^2,x^3）来拟合更复杂的曲线，但其本质仍是线性模型（因为对参数 w 而言是线性的）。
正则化：为了防止过拟合（模型在训练集上表现很好，在测试集上很差），可以在损失函数中加入惩罚项。
- L1正则化（Lasso）：倾向于产生稀疏权重，可用于特征选择。
- L2正则化（Ridge）：使权重值普遍变小，但不会为0。