几种常用的排序算法

最新推荐文章于 2021-12-11 21:44:57 发布

原创最新推荐文章于 2021-12-11 21:44:57 发布 · 366 阅读

CC 4.0 BY-SA版权

1.排序的基本概念和分类

所以,什么是排序？

假设含有n个记录的序列，其相应的关键字分别为{k1,k2,k3…kn}，需要确定1，2，3…n的一种排列p1,p2,p3…pn，使其相应的关键字满足Kp1 <= Kp2 <= Kp3 <=…<= Kpn（非递减或非递增）关系，使得序列成为一个按照关键字有序排列的序列，这样的操做就是排序；

排序的稳定性

假设Ki=Kj(1<=i<=n,1<=j<=n,i=j)，且在排序前的序列中Ri领先于Rj(即r<j)。如果排序后，Ri仍然小于Rj，则称这种排序法是稳定的；

内排序和外排序

内排序是在整个排序过程中，待排序的所有记录全部被放置在内存中；外排序是由于排序记录个数太多，不能同时放置在内存中，整个排序需要内外存之间多次交换数据才能进行；

2.几个简单的排序

2.1.选择排序

选择排序就是通过n-1次关键字之间的比较，从n-i+1个记录中选出关键字最小的记录，并和第i个记录之间交换；
如图所示代码实现

for(int i=0;i<arr.length-1;i++){
	for(int j=i+1;j<arr.length;j++){
		if(arr[i]>arr[j]){
			int temp=arr[i];
			arr[i]=arr[j];
			arr[j]=temp;
		}
	}
}

2.2.冒泡排序

冒泡排序是一种交换排序，它的基本思想是：两两比较相邻的元素，如果反序则交换，直到没有反序元素；
在这里插入图片描述代码实现：

for(int i=0;i<arr.length-1;i++){
	for(int j=1;j<arr.length-i;j++){
		if(arr[j]<arr[j-1]) {
					temp=arr[j-1];
					arr[j-1]=arr[j];
					arr[j]=temp;
		}
	}
}

但是这样我们会发现每次开销太大，而且还有一个规律就是：
在这里插入图片描述我们在排序的时候，每次都会遍历一遍数组，但是我们会发现，我们在实现过程中，如果在每一次i遍历之后的j遍历过程中，如果没有发生交换，则包括j+1之后的操作也不需要交换所以我么可以在此处进行优化：

int count=0;
int temp=0;
for(int i=0;i<arr.length-1;i++){
	count=0;
	temp=arr[0];
	for(int j=1;j<arr.length-i;j++){
		if(arr[j]<temp){
			arr[j-1]=arr[j];
			count++;
		}else{
			arr[j-1]=temp;
			temp=arr[j];
		}
	}
	if(count==0){
		break;
	}
}

2.3.插入排序

插入排序的基本操作就是将一个元素插入到已经排好序的有序表中，从而得到一个新的、记录数增1的有序表；
在这里插入图片描述代码实现：

int temp=0;
for(int i=1;i<arr.length;i++){
	for(int j=i;j>0&&arr[j-1]>arr[j];j--){
		temp=arr[j];
		arr[j]=arr[j-1];
		arr[j-1]=temp;
	}
}

与冒泡排序有些类似，插排的原理是向前遍历，如果有逆序的则交换，否则会一直遍历直到一轮的结束，所以我们可以做出如下的优化：
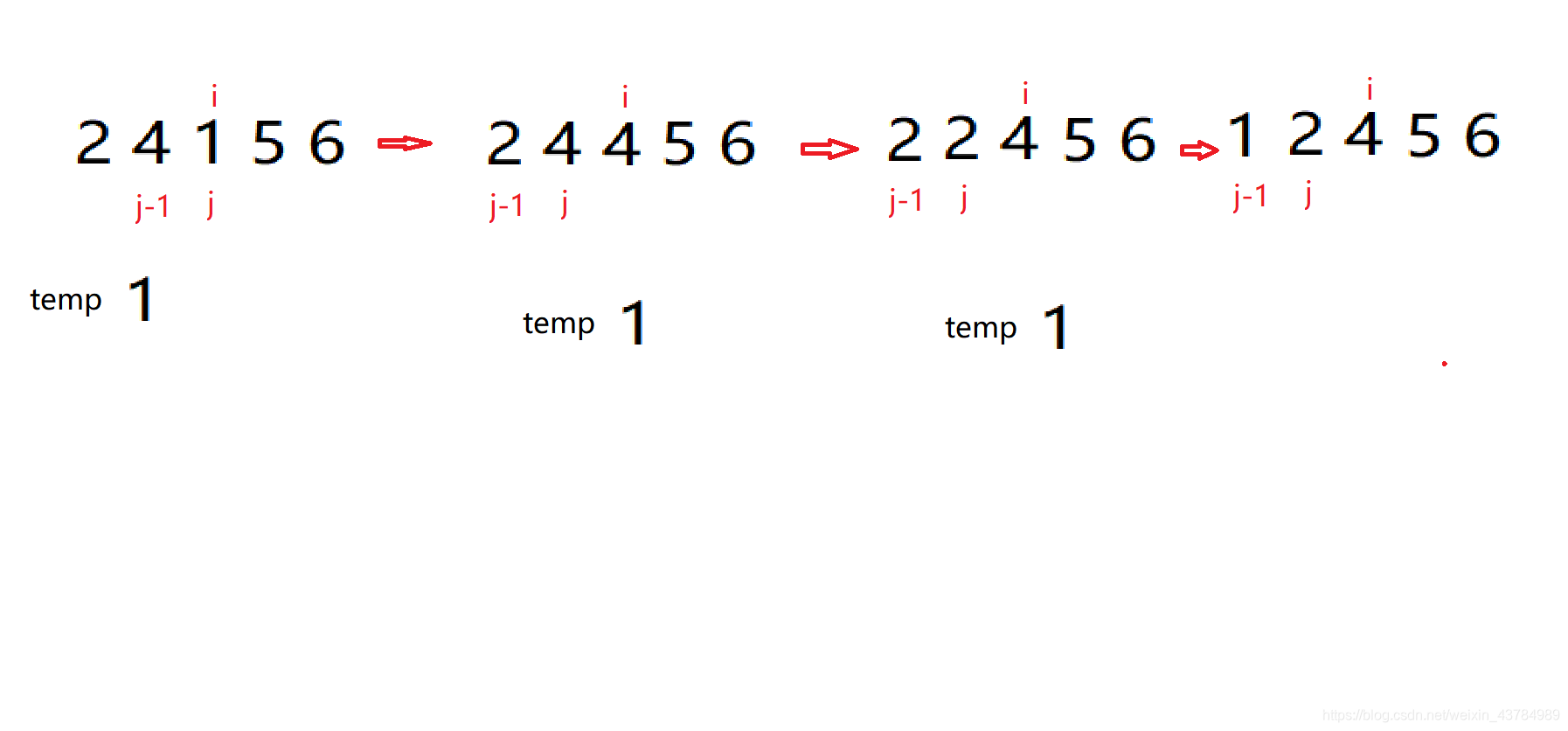在这里插入图片描述先定义一个变量temp=arr[i],只需要将arr[j-1]付给arr[j],等到j-1=0的时候一轮循环结束，在将temp付给arr[j-1]即可；这样减少了交换的步骤，节省时间；

for(int i=1;i<arr.length;i++){
	int temp=arr[i];
	int j=0;
	for(j=i;j>0&&arr[j-1]>temp;j--){
		arr[j]=arr[j-1];
	}
	arr[j]=temp;
}

3.归并排序

归并排序就是利用归并的思想实现的排序方法。它的原理是假设初始序列含有n个元素，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到[n/2]个长度为2或为1的子序列，然后再次两两归并…如此重复，得到一个长度为n的有序序列为止，这种方法称为2路归并排序；

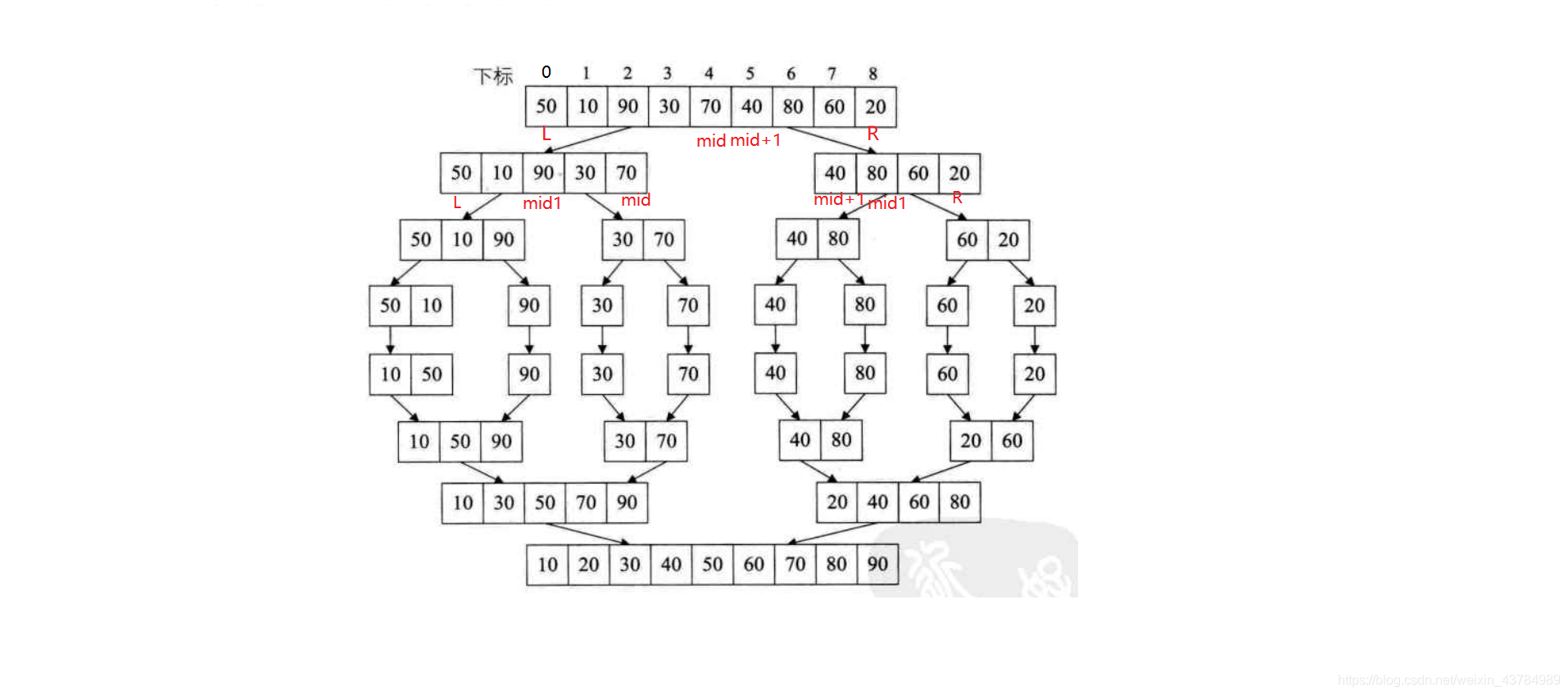
在这里插入图片描述

步骤：
1.我们的目的就是将数组{50，10，90，30，70，40，80，60，20}进行排序；
2.先将数组二分，计算出L,R,mid=(L+R)/2;
3.在将数组按照{50,10,90,30,70}和{40,80,60,20}二分；
4.在两个新的二分数组中在按照步骤2依次循环计算；
5.当L>=R时候停止二分，向上归并-如下图就是二分和归并的比较可以清晰的看出，归并就是逆二分；
在这里插入图片描述 6.直到递归完成，排序就完成了；
代码实现：

main(){
	megerSort(arr,0,arr.length-1);
}
public void megerSort(int []arr,int l,int r){
	if(l>=r){
		return;
	}
	int mid=(l+r)/2;
	mergeSort(arr,l,mid);
	mergeSort(arr,mid+1,l);
	merge(arr,l,mid,r);
}
private void mergr(int[]arr,int l,int mid,int r){
	int []aux=new int[r-l+1];
	for(int i=l;i<=r;i++){
		aux[i-l]=arr[i];
	}
	int i=l;int j=mid+1;
	for(int k=l;k<=r;k++){
		if(i>mid){
			arr[k]=aux[j-l];
			j++;
		}else if(j>r){
			arr[k]=aux[i-l];
			i++;
		}else if(arr[i-l]<=arr[j-l]){
			arr[k]=aux[i-l];
			i++;
		}else{
			arr[k]=aux[j-l];
			j++;
		}
	}
}

当然这不是最完美的归并排序，还有其可以优化的地方：
优化方案：
1.根据时间复杂度的分析，在数组长度（即元素个数）不是足够大的时候，使用简单的插入排序的耗时会更低，所以第一处的优化在于,我们不再需要当l>=r的时候结束函数，我们只需要限定一个值，使元素在这个区间内直接使用插入排序：

if(l-r<15){
	//调用插入排序
}

2.不知道你们有没有发现，在merge()函数中，如果arr[mid]<arr[mid+1],即左半边的数组元素总是小于右半边的，之间可以不用在进行归并；所以可以加一个限定条件：

if(arr[mid]>arr[mid+1]){
	merge(arr,l,mid,r);
}

4.堆排序

堆排序就是利用最大堆/最小堆进行的排序，这里就不多讲了；

5.快速排序(2路快排)

快速排序的基本思想是：通过一趟排序将待排序的元素分割成独立的几部分（2部分或3部分），其中一部分记录的元素均比另一部分的元素小，则这两部分元素继续排序，已达到整个序列有序的目的；首先要做的就是选取一个元素作为关键字，将其放到一个合适的位置，使该元素左边的都比它小，右边的都比他大。

public static void main(Stirng[] args){
	quickSort(arr,0,arr.length-1);
}
private static void quickSort(int []arr,int l,int r){
	if(l>=r){
		return;
	}
	int p=partiton(arr,l,r);
	quickSort(arr,l,p-1);
	qucikSort(arr,p+1,r);
}

根据上述代码，最关键的就是partition函数，用来计算出关键字的位置；以数组{2,3,7,1,4,6,9}为例：
在这里插入图片描述选择arr[l]，即2作为关键字key，利用for循环定义i指针从l+1开始，如果arr[i]>key，则放到j+1的位置，i++（由for循环控制i），到第一轮循环完成之前应该保证key关键字左边的都小于key，右边的都大于key：
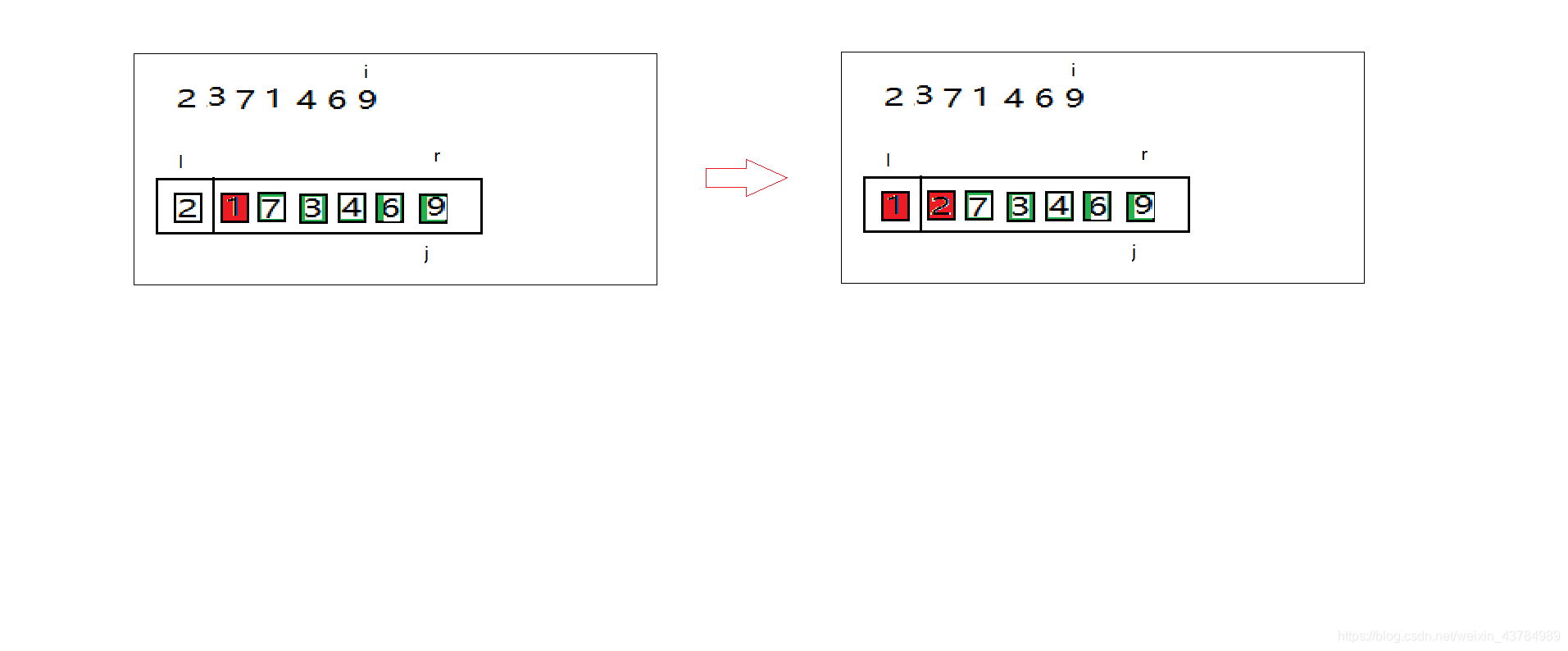到最后将key和l+1交换即可，这样第一轮排序就完成；以此类推，第二轮，第三轮。。。第n轮排序完成；下面的代码就是如何实现partition函数：

public static int partition(int[]arr,int l,int r){
	swap(arr,arr[l],(int)(Math.random()*(r-l)));
	int v=arr[l];
	int j=l;
	for(int i=l+1;i<=r;i++){
		if(arr[i]<=v){
			swap(arr,i,j+1);
			j++;
		}
	}
	swap(arr,l,j);
	return j;
}

So?你以为这就完了？错了，这才是快排刚刚开始，上述代码实现的快排叫做二路快排，耗时长而、开销大、效率低，所以我们可以对其在进行一些修改:

public static void main(String[] args){
	quickSort2(arr,0,arr.length-1);
}
public static void quickSort2(int [] arr,int l,int r){
	if(r-l<15){
		//调用插入排序
		InsertSort.insertSort(arr,l,r);
		return;
	}
	int p=partition2(arr,l,r);
	quickSort2(arr,l,p-1);
	quickSort2(arr,p+1,r);
}
private static int partition2(int []arr,int l,int r){
	swap(arr,arr[l],(int)(Math.random()*(r-l)));
	int v=arr[l];
	int i=l+1;
	int j=r;
	while(true){
		while(i<=r&&arr[i]<v){
			i++;
		}
		while(j>l&&arr[j]>=v){
			j--;
		}
		if(i>j){
			break;
		}
		swap(arr,i,j);
		i++;
		j--;
	}
	swap(arr,l.j);
	return j;
}

6.快速排序（3路快排）

不知道大家有没有注意到，在二路快排中每次对元素的判断时将等于该关键字key的元素都归到或是>=里面，或是<=里面，因为这样，二路快排的效率很低；所以，我们可以将=key的元素划分出来一部分单独处理；
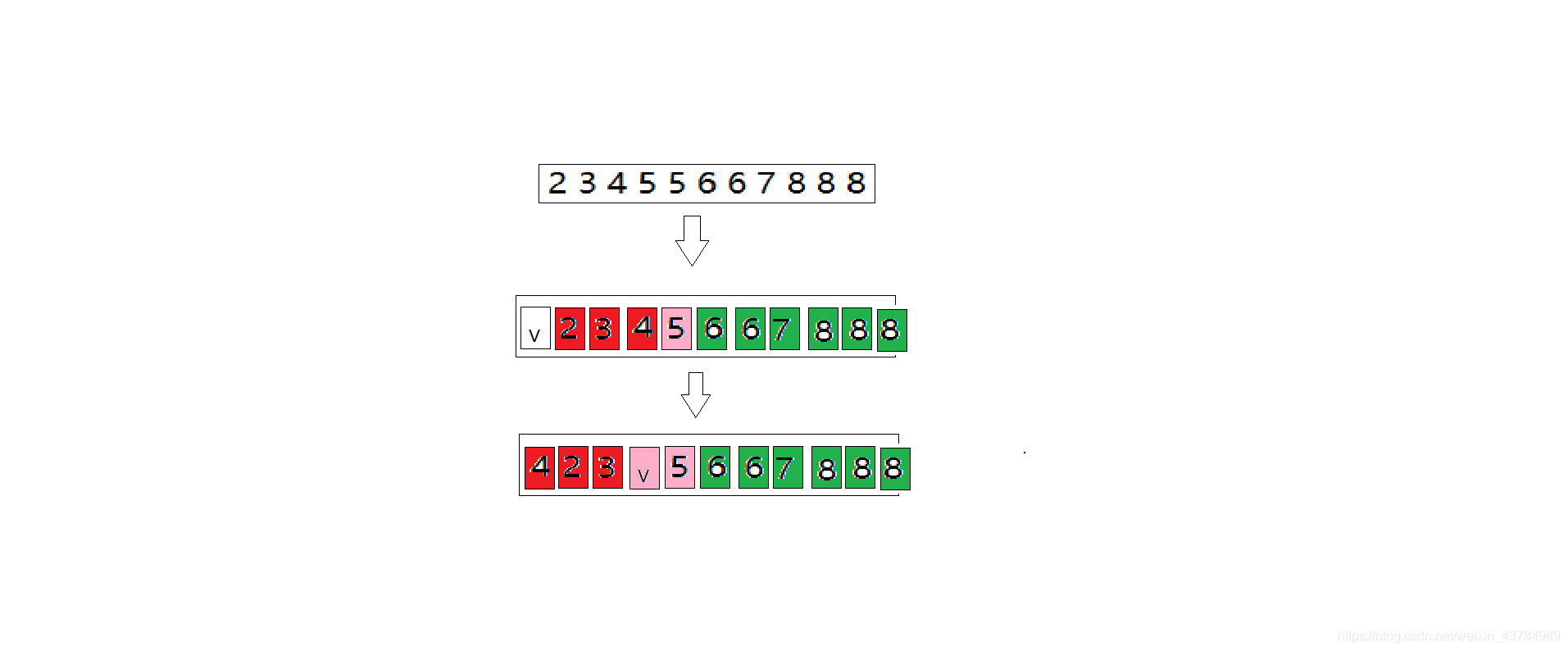在这里插入图片描述如图，以该数组为例，取关键字v=5，小于5的放在左边为红色，等于5的放在中间为粉色，大于5的放在右边为绿色；（此图不是一轮快排之后的正确解，这里只是作为演示）

public static void main(String[] args){
	quickSort3(arr,0,arr.length-1);
}
public static void quickSort3(int [] arr,int l,int r){
	if(r-l<15){
	//调用插入排序
		InsertSort.insertSort(arr,l,r);
	}
	int p=partition3(arr,l,r);
	qucikSort3(arr,l,p-1);
	quickSort3(arr,p+1,r);
}
private static int partition3(int []arr,int l,int r){
	swap(arr,l,(int)(Math.random(r-l)));
	int v=arr[l];
	int lt=l;
	int i=l+1;
	int gt=r+1;
	while(i<gt){
		if(arr[i]<v){
			swap(arr,lt+1,i);
			lt++;
			i++;
		}else if(arr[i]>v){
			swap(arr,gt-1,i);
			gt--;
		}else{
			i++;
		}
	}
	swap(arr,lt,l);
	return lt+1;
}

7.计数排序

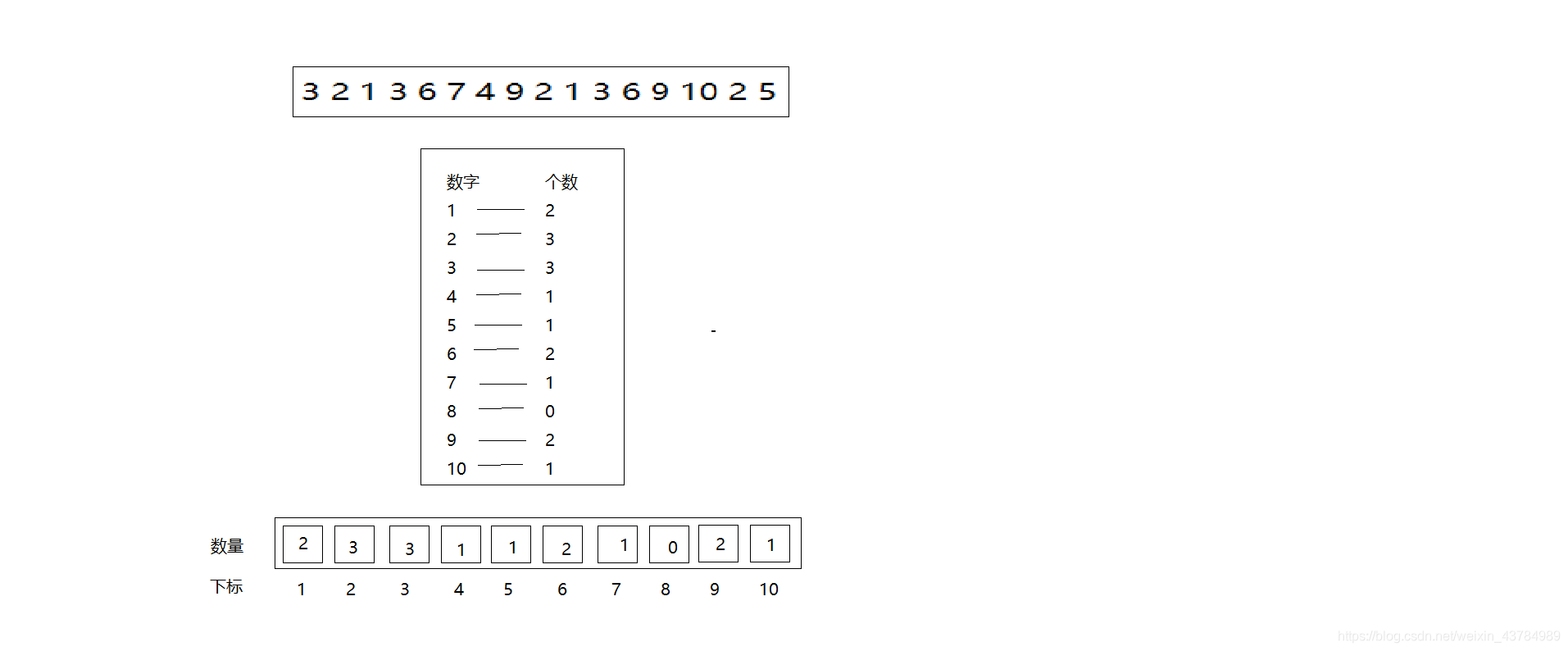
计数排序类似于哈希表，其原理在于选取一个合适的连续存储空间(一维数组)用来存放数字，每个数组元素的下标表示元素的大小，数组中的元素表示该位置元素的个数；最后再利用遍历得到一个有序数组；
在这里插入图片描述


public static void main(String[] args){
	CountSort(arr);
}
private void CountSort(int []arr){
	int max=findMax(arr);		//找出数组中的最大值
	int min=findMin(arr);		//找出数组中的最小值
	int [] count=new int[max-len+1];
	for(int i=0;i<arr.lengtj;i++){
		count[arr[i]-min]++;
	}
	int index=0;
	for(int i=0;i<count.length;){
		if(count[i]!=0){
			arr[index]=i+min;
			count[i]--;
			index++;
			continue;
		}else{
			i++;
		}
	}
}