大话数据结构（2.二分搜索树）

1.树结构

1.1.树的定义

树（tree）是n(n>=0)个结点的有限集合。n=0时为空树。在任意一棵非空树中：(1)有且只有一个特定的称为root的根结点(2)当n>1的时候，其余结点可分为m个互不相交的有限子集,其中每一个集合本身又是一个树，并且称为根的子树。

强调两点：
1.n>0时根节点是唯一的
2.m>0时子树的个数没有限制，但一定是互不相交的

1.1.1.结点定义

树的结点包含一个数据元素和若干个指向其子树的分支。结点拥有的子树个数称为结点的度。度为0的结点称为叶子节点/终端节点；度不为0的结点称为分支结点。树的度是树内各结点的度的最大值。

1.1.2.结点之间的关系

结点的子树的根称为该节点的孩子结点，相应的该节点称为孩子的父亲结点。
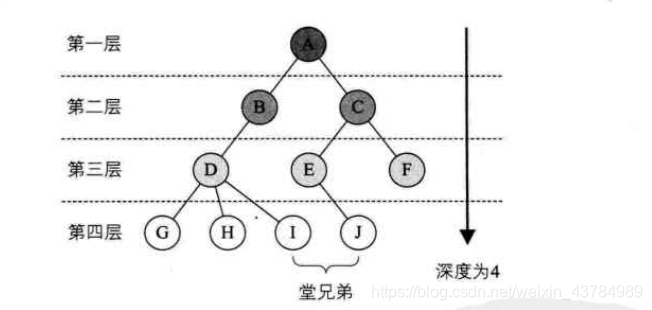
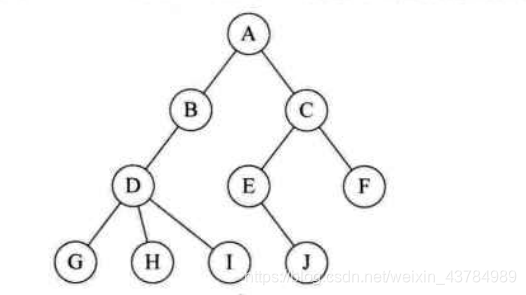
比如上图中：A叫做B&C的父亲结点。相应的B&C叫做A的孩子结点。

1.1.3.树的其他概念

1.树的层次
结点的层次(Level)从根开始定义，根为第一层，根的孩子为第二层。树中结点的最大层次称为树的深度。

1.2.二叉树

1.2.1.二叉树的定义

二叉树是n个结点的有限集合，该集合或者为空集（成为空二叉树），或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。

1.2.2.二叉树的特点

1.每个节点最多只有两个子树，所以二叉树中不存在度大于2的结点；
2.左子树和右子树的顺序是一定的，不能随意更改；
3.即使树中的某结点只有一棵子树，也要区分是左子树还是右子树；

所有二叉树具有五种形态：
1.空二叉树
2.只有一个根节点
3.根节点只有左子树
4.根节点只有右子树
5.根节点既有左子树又有右子树；

1.2.3.特殊的二叉树

1.2.3.1.斜树

所有结点都只有左子树或者都只有右子树的二叉树。其实链表也可以看成是斜树；

1.2.3.2.满二叉树

在一棵二叉树上，如果所有的分支结点都存在左子树和右子树，并且所有的叶子都在同一层上，这样的树叫做满二叉树；

满二叉树的特点：
1.叶子只能出现在最下一层
2.非叶子结点的度一定是2
3.在同样深度的二叉树中，满二叉树的结点最多，叶子最多；

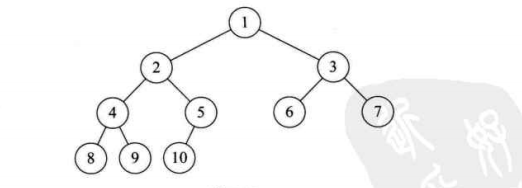
1.2.3.3.完全二叉树

对一棵具有n结点的二叉树按照层次编号，如果编号为 i (1<=i<=n) 的结点与同样深度的满二叉树中编号为 i 的结点在二叉树中位置完全相同，则这棵二叉树称为完全二叉树；

完全二叉树的特点：
1.叶子节点只能出现在最下面的两层
2.最下层的叶子一定集中在左部连续位置de sh> 倒数二层，若有叶子结点，一定都在右部连续
4.如果结点度为1，则该节点只有左孩子
5.同样结点的二叉树，完全二叉树深度最小

1.2.3.4.区分满二叉树和完全二叉树

1.满二叉树一定是完全二叉树，但完全二叉树不一定是满二叉树；
2.完全二叉树的所有结点与同样深度的满二叉树，他们按层序编号相同的结点是一一对应的；

1.2.4.二叉树的性质

1.2.4.1.性质1

在二叉树的第 i 层上至多有2^(i-1)个结点；

1.2.4.2.性质2

深度为K的二叉树最多有2^k -1个结点；

1.2.4.3.性质3

对任何一个二叉树T，如果其终端结点树为m，度为2的结点数为n，则m=n+1；
终端结点数其实就是叶子结点数，而一个二叉树，除了叶子节点外，剩下的就是度为1或2的结点，我们设n1为度为1的结点数，n2为度为2的结点数，则总结点数T=n+n1+n2;
最终我们可以推出：
终端节点数N=度为2的结点数M+1；

1.2.4.4.性质4

具有n个结点的完全二叉树的深度为|log2 ^ n|+1；(|x|表示不大于x的最大整数)

1.如果i=1，则结点i是二叉树的根，无双亲；
2.如果2i>n，则i无左孩子；否则左孩子是结点2i；
3.如果2i+1>n，则结点i无左右孩子；否则其右结点是结点2i+1；

1.3.对二叉树的操作

定义二叉树的类和构造函数：

public class BinarySearchTree<E extends Comparable<E>> {//二分搜索树的元素具有可比较性
	private Node root;
	private int size;
	public BinarySearchTree() {
		root=null;
		size=0;
	}
	private class Node{
		public E e;
		public Node left;
		public Node right;
		public Node(E e) {
			this.e=e;
			left=null;
			right=null;
		}
	}

1.3.1.遍历二叉树

1.3.1.1.前序遍历（DLR）（深度优先）

遍历规则：若二叉树为空，则空操作返回，否则先访问根节点，然后再前序遍历左子树，在遍历右子树；

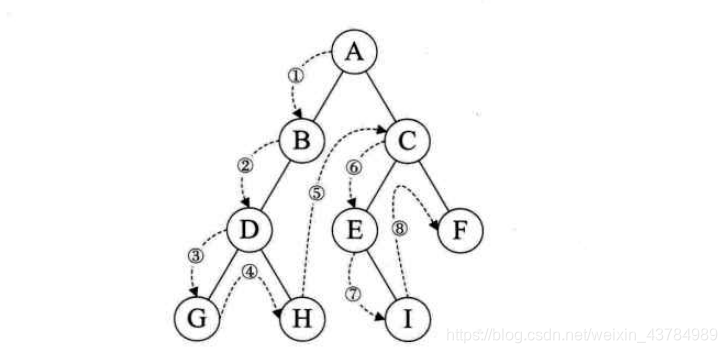
public void beforOrder() {
		ArrayList<E> list=new ArrayList<>();
		befor(root,list);
	}
	private void befor(BinarySearchTree<E>.Node node, ArrayList<E> list) {
		if(node==null) {
			return;
		}
		list.add(node.e);
		befor(node.left, list);
		befor(node.right, list);
	}

1.3.1.2.中序遍历（LDR）（深度优先）

遍历规则：若树是空，则空操作返回；否则从根节点开始（注意并不是先访问根节点），中序遍历根节点的左子树，然后访问根结点，在访问右子树；所以中序遍历是由小到大遍历；

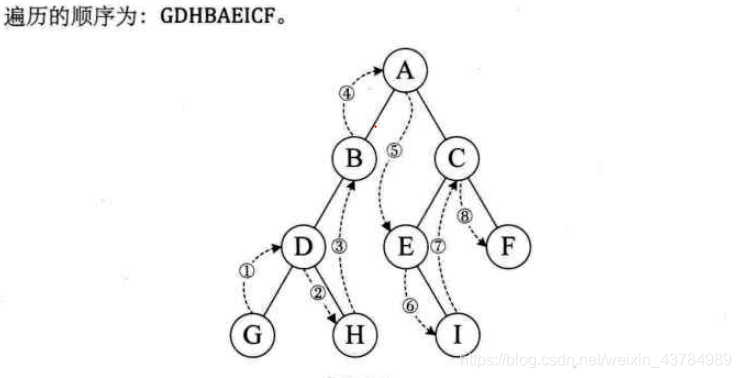
public void inOrder() {
		ArrayList<E> list=new ArrayList<E>();
		inOrder(root,list);
	}
	private void inOrder(BinarySearchTree<E>.Node node, ArrayList<E> list) {
		if(node==null) {
			return;
		}
		inOrder(node.left,list);
		list.add(node.e);
		inOrder(node.right,list);
	}

1.3.1.3.后序遍历（LRD）（深度优先）

遍历规则：若树为空，返沪空操作；否则从根结点开始，先访问左右子树，在访问根结点；

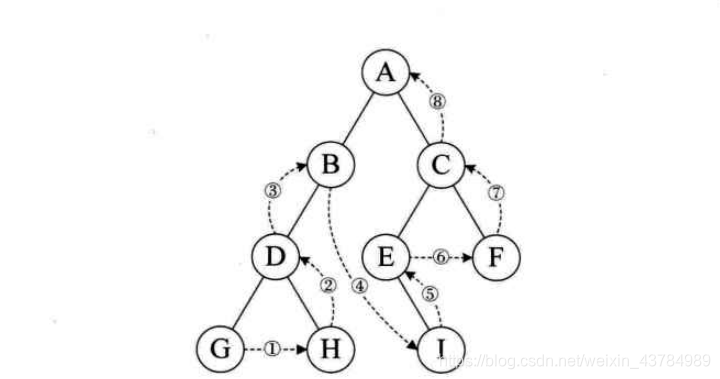
public void behind() {
		ArrayList<E> list=new ArrayList<>();
		behind(root,list);
	}
	private void behind(BinarySearchTree<E>.Node node, ArrayList<E> list) {
		if(node==null) {
			return;
		}
		behind(node.left,list);
		behind(node.right,list);
		list.add(node.e);
	}

1.3.1.4.层序遍历（广度优先）

规则是：若结点为空，则返回空操作，否则从树的第一层也就是根节点开始访问，从上而下逐层遍历，在同一层中，按照从左到右的顺序对结点进行逐个访问；

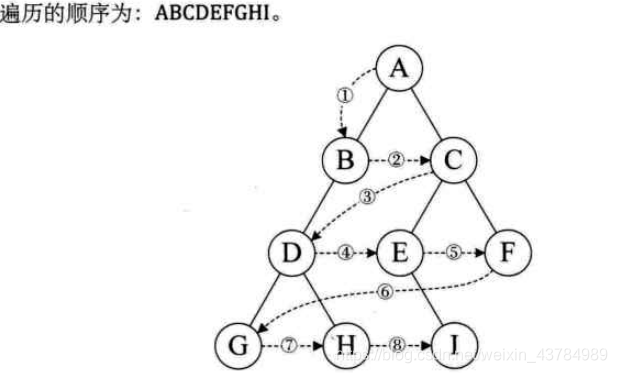
public void levelOrder() {
		ArrayList<E> list=new ArrayList<>();
		Queue<Node> qe=new LinkedList<>();
		qe.add(root);
		while(!qe.isEmpty()) {
			Node cur=qe.poll();
			list.add(cur.e);
			if(cur.left!=null) {
				qe.add(cur.left);
			}if(cur.right!=null){
				qe.add(cur.right);
			}
		}
		System.out.println(list);
	}

1.3.2.增删改查

1.3.2.1.添加元素

private Node add(Node node ,E e) {
		if(node==null) {
			size++;
			return new Node(e);
		}
		if(e.compareTo(node.e)>0) {
			node.right=add(node.right,e);
		}else if(e.compareTo(node.e)<0) {
			node.left=add(node.left,e);
		}
			return node;		
	}

1.3.2.2.获取最大元素

public E maxmum() {
		if(size==0) {
			throw new IllegalArgumentException("Tree is empty");
		}
		return maxmum(root).e;
	}
	private  Node maxmum(Node node) {
		if(node.right==null) {
			return node;
		}
		return maxmum(node.right);
	}

1.3.2.3.获取最小元素

public E minmum() {
		if(size==0) {
			throw new IllegalArgumentException("Tree is empty");
		}
		return minmum(root).e;
	}
	private Node minmum(BinarySearchTree<E>.Node node) {
		if(node.left==null) {
			return node;
		}
		return minmum(node.left);
	}

1.3.2.4.删除元素

1.3.2.4.1.删除最大元素

public E removemax() {
		E e=maxmum();
		root=removemax(root);
		return e;
	}
	private Node removemax(Node node) {
		if(node.right==null) {
			Node leftNode=node.left;
			node.left=null;
			size--;
			return leftNode;
		}
		node.right=removemax(node.right);
		return node;
	}

1.3.2.4.2.删除最小元素

public E removemin() {
		E e=minmum();
		root=removemin(root);
		return e;
	}
	private Node removemin(Node node) {
		if(node.left==null) {
			Node rightNode=node.right;
			node.right=null;
			size--;
			return rightNode;
		}
		node.left=removemin(node.left);
		return node;
	}

1.3.2.4.3.删除任意元素

public void remove(E e) {
		root=remove(root,e);
	}
	private Node remove(Node node,E e) {
		if(node==null) {
			return null;
		}
		if(e.compareTo(node.e)>0) {
			node.right=remove(node.right,e);
			return node;
		}else if(e.compareTo(node.e)<0) {
			node.left=remove(node.left,e);
			return node;
		}else {
			if(node.left==null) {
				Node rightNode = node.right;
				node.right=null;
				size--;
				return rightNode;
			}
			if(node.right==null) {
				Node leftNode = node.left;
				node.left=null;
				size--;
				return leftNode;
			}
			Node suc=minmum(node.right);
			suc.right=removemin(node.right);
			suc.left=node.left;
			node.left=null;
			return suc;
		}