HDU - 2050 折线分割平面详解

最新推荐文章于 2020-01-05 09:50:11 发布

原创最新推荐文章于 2020-01-05 09:50:11 发布 · 755 阅读

0 ·

CC 4.0 BY-SA版权

ACM递推专栏收录该内容

1 篇文章

订阅专栏

本文深入探讨了使用折线分割平面的最大数目问题，通过对比直线分割平面的数学模型，提出了针对折线情况的计算公式，并附带了C语言实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

折线分割平面详解

Problem Description

我们看到过很多直线分割平面的题目，今天的这个题目稍微有些变化，我们要求的是n条折线分割平面的最大数目。比如，一条折线可以将平面分成两部分，两条折线最多可以将平面分成7部分，具体如下所示。

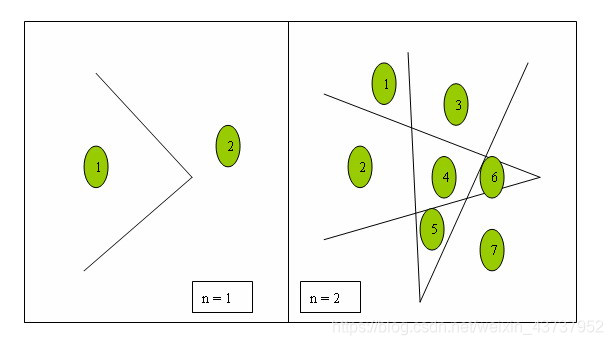
Input

输入数据的第一行是一个整数C,表示测试实例的个数，然后是C 行数据，每行包含一个整数n(0<n<=10000),表示折线的数量。

Output

对于每个测试实例，请输出平面的最大分割数，每个实例的输出占一行。

Sample Input

Sample Output

本题一眼看上去比较复杂，但我们可以从简单的直线的情况入手

当用直线分割平面时，若想要所分割平面数量最多，则不能存在三条或三条以上直线相交于一点的情况，故第n(1 <= n )条直线会增加n - 1个点，增加n个平面。公式为F(n) = 1 + 1 + 2 + 3 + 4 + .... + n = 1 + n * ( n + 1) / 2。

下面考虑折线的情况。

每当添加第n条折线时，平面上已有2 * (n - 1)条直线，所以最多能4 * (n - 1) 个交点（注意！折线本身的交点不算），则当添加第n条折线时能获得

4 * (n - 1) + 1个平面。所以F(n) = 1 + 1 + 5 + .... + 4 * (n - 1) + 1 = 2 * n * n - n + 1;

以下是代码

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<string>
#include<queue>
#include<utility>
#include<vector>

int main(int argc, char const *argv[])
{
    int t;
    scanf("%d", &t);

    while(t--){
        int n;
        scanf("%d", &n);
        printf("%d\n", 2 * n * n - n + 1);
    }

    return 0;
}