COMP9101 算法设计 week3

FFT快速傅立叶

假设我们有2个多项式:
PA(x) = Anx^n…+A0. PB(x)=Bnx ^n+…+B0

1. 将他们变成value表示法：
   因为它们两个的乘积是2n阶的，我们需要2n+1个不同的x：
   PA(x)<-> {(x0,PA(x0)),…(x2n, PA(x2n))}
   PB(x)<->{(x0,PB(x0)),…,(x2n, PB(x2n))}

2.将它们点对点相乘
{(x0, PA(x0)*PB(x0)), (x1,PA(x1)PB(x1))…(x2n, PA(x2n)PB(x2n))}

3.我们将PC(x)代入：
PC(x)=C(2n)x^2n+C(2n-1)x ^2n-1…+C1x+C0

在K算法时，x的取值是-n到n，但当n很大的时候会爆炸。
方式一是变成复数。

复数

z=a+ib, 也可以表示为模 |z|=√(a ^ 2+b ^ 2) 和辐角arg(z)—>取值为(-π，π], 并且满足:
z=|z|eiarg(z) =|z|(cosarg(z)+isinarg(z))

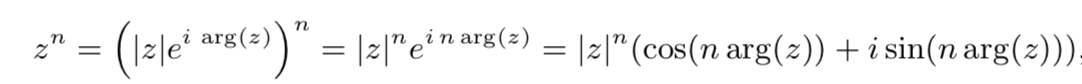
单位根

单位根的阶n是复数且满足z^n=1.
如果z^ n = |z|^n (cos(n arg(z)) + i sin(n arg(z))) = 1,
则|z|=1 并且 n个 arg(z)是2π的倍数。
所以， narg(z)=2πk, 即arg(z)=2πk/n. k的范围是0～n-1.
我们让 ωn = e ^(i2π/n)—>k=1, ω被称是n阶单位原根。