概念:
将一个数组分成一段一段,用树状的数组将其储存。
大概如此
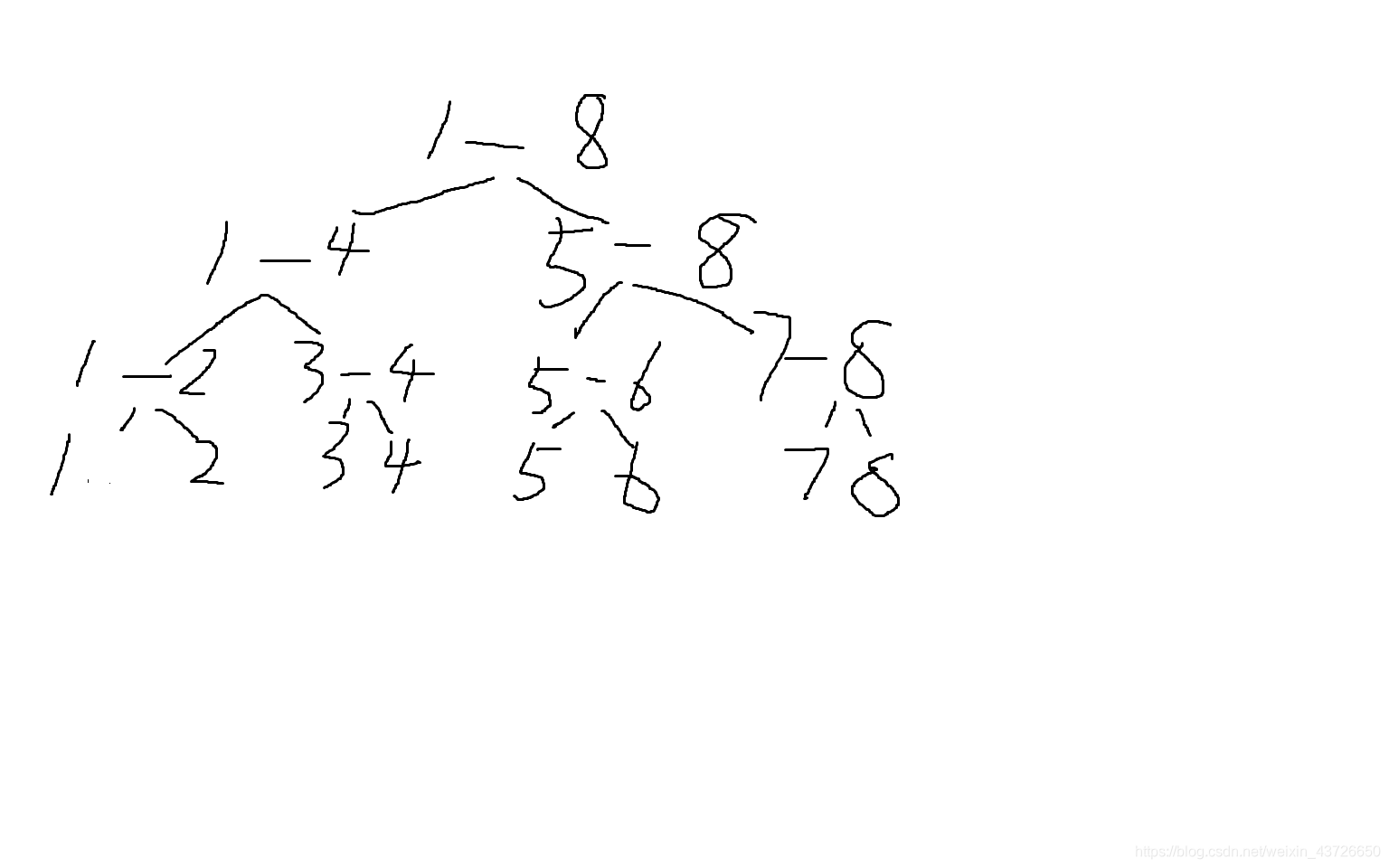
操作:
单点修改:从根节点一直遍历到叶子节点
单点查询:同单点修改
区间查询:因为线段树的每一个节点都是一个区间,所以我们只需将查询的区间分为几个在线段树节点上的区间就行了
区间修改:重要的是懒标记,也就是说,当修改一个区间的时候,我们只需要修改几个大的区间,并将值保留下来,
在需要用到小区间的时候再去修改
代码(因方便给出的是区间修改和查询的板子):
#include<iostream>
#include<cstdio>
using namespace std;
#define int long long
void read(long long &x)
{
x=0;
long long f=1;
char c=getchar();
while('0'>c||c>'9')
{
if(c=='-')
f=-1;
c=getchar();
}
while('0'<=c&&c<='9')
{
x=(x<<3)+(x<<1)+c-'0';
c=getchar();
}
x*=f;
}
void write(long long x)
{
if(x<0)
{
putchar('-');
write(-x);
return;
}
if(x<10)
putchar(x+'0');
else
{
write(x/10);
putchar(x%10+'0');
}
}
struct node
{
int l;
int r;
long long s;
long long lazy;
}a[4000005];
long long n,q;
long long c;
long long p,v;
long long _l,_r;
void build(int k,int l,int r)
{
a[k].l=l;
a[k].r=r;
a[k].lazy=0;
if(l==r)
{
read(a[k].s);
return;
}
int mid=(l+r)>>1;
build(k<<1,l,mid);
build(k<<1|1,mid+1,r);
a[k].s=a[k<<1].s+a[k<<1|1].s;
}
void change(int k,int l,int r,long long v)
{
if(a[k].l>r||a[k].r<l)
return;
if(l<=a[k].l&&a[k].r<=r)
{
a[k].lazy+=v;
a[k].s+=(a[k].r-a[k].l+1)*v;
return;
}
a[k<<1].s+=(a[k<<1].r-a[k<<1].l+1)*a[k].lazy;
a[k<<1|1].s+=(a[k<<1|1].r-a[k<<1|1].l+1)*a[k].lazy;
a[k<<1].lazy+=a[k].lazy;
a[k<<1|1].lazy+=a[k].lazy;
a[k].lazy=0;
change(k<<1,l,r,v);
change(k<<1|1,l,r,v);
a[k].s=a[k<<1].s+a[k<<1|1].s;
}
long long summ(int k,int l,int r)
{
if(l<=a[k].l&&a[k].r<=r)
return a[k].s;
if(a[k].lazy!=0)
{
a[k<<1].s+=(a[k<<1].r-a[k<<1].l+1)*a[k].lazy;
a[k<<1|1].s+=(a[k<<1|1].r-a[k<<1|1].l+1)*a[k].lazy;
a[k<<1].lazy+=a[k].lazy;
a[k<<1|1].lazy+=a[k].lazy;
a[k].lazy=0;
}
if(a[k].l>r||a[k].r<l)
return 0;
long long summ__=0;
summ__+=summ(k<<1,l,r);
summ__+=summ(k<<1|1,l,r);
return summ__;
}
#undef int
int main()
{
read(n);
read(q);
build(1,1,n);
for(int i=1;i<=q;i++)
{
read(c);
if(c==1)
{
read(_l);
read(_r);
read(v);
change(1,_l,_r,v);
}
if(c==2)
{
read(_l);
read(_r);
write(summ(1,_l,_r));
putchar('\n');
}
}
return 0;
}























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








