1. 条件概率
-
已知某个条件发生,另一件事的概率。
-
例子:明天下雨的概率是30%(无条件概率),但如果今天阴天,明天下雨的概率变成60%——这就是条件概率。
-
-
公式:
P(下雨|阴天) = 60% -
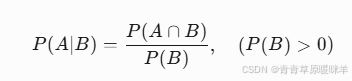
2. 贝叶斯定理
-
用新信息更新概率。比如检测出阳性,实际得病的概率是多少?
-
例子:
-
疾病发病率1%,检测准确率99%(得病时阳性概率99%,健康时阴性概率99%)。
-
若检测为阳性,真实得病概率 ≈ 50%(因为健康人1%被误检为阳性,人数远多于真实患者)。
-
-
-
公式:
P(病|阳性) = [P(阳性|病) * P(病)] / P(阳性) -
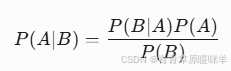
二、常见概率分布
1. 高斯分布(正态分布)
-
通俗解释:
“中间多,两边少”的对称分布,比如人类身高、考试分数。-
参数:均值(中心位置)、方差(数据分散程度)。
-
公式:钟形曲线
P(x) = (1/σ√(2π)) * e^(-(x-μ)^2/(2σ²)) -
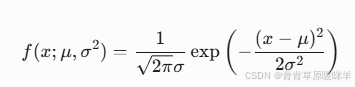
-
2. 伯努利分布
-
通俗解释:
一次二选一试验,比如抛硬币(正面1,反面0)。-
参数:p(正面概率)。
-
公式:
P(x=1)=p,P(x=0)=1-p -
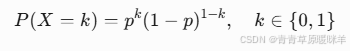
-
3. 泊松分布
-
通俗解释:
固定时间内事件发生次数的概率,比如奶茶店每小时来5个顾客的概率。-
参数:λ(平均发生次数)。
-
公式:
P(k次) = (λ^k * e^-λ) / k! -
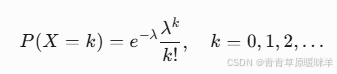
-
4. 指数族分布
-
通俗解释:
一类分布的统一表达式(包括高斯、伯努利、泊松等),方便数学处理。-
例子:逻辑回归假设数据服从伯努利分布(属于指数族)。
-
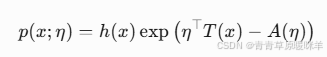
三、期望、方差、协方差
1. 期望(均值)
-
通俗解释:
长期平均结果。比如赌博的期望收益是-10元,说明长期玩会亏钱。-
公式:
E[X] = Σ(x_i * P(x_i))
-
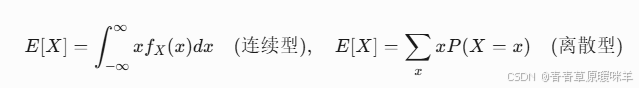
2. 方差
-
通俗解释:
数据的波动程度。比如股票A方差小(稳定),股票B方差大(暴涨暴跌)。-
公式:
Var(X) = E[(X - E[X])²]
-
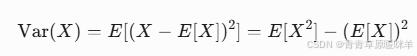
3. 协方差与相关系数
-
通俗解释:
-
协方差:两个变量如何一起变化。比如身高和体重通常协方差为正(高的人更重)。
-
相关系数:标准化后的协方差(范围-1到1),-1表示完全负相关。
-
公式:
Cov(X,Y) = E[(X-E[X])(Y-E[Y])]
-
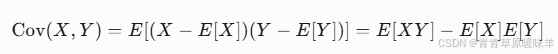
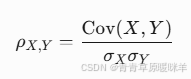
四、统计推断
1. 假设检验
-
通俗解释:
判断数据是否支持某个假设。比如新药是否有效。-
步骤:
-
假设“新药无效”(零假设)。
-
计算p值(假设成立时,观察到当前数据的概率)。
-
若p值<5%,拒绝零假设,认为药有效。
-
-

2. 置信区间
-
通俗解释:
估计参数的“可信范围”。比如全校平均身高95%置信区间是[160cm, 165cm],说明有95%把握真实均值在此区间内。

3. 最大似然估计(MLE)
-
通俗解释:
根据数据猜最可能的参数。比如抛硬币10次出现7次正面,估计正面概率p=70%。-
公式:
p = argmax( P(数据|p) )
-
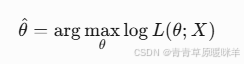
4. 最大后验估计(MAP)
-
通俗解释:
MLE + 先验知识。比如已知硬币正常,即使10次出现7次正面,估计p≈55%。-
公式:
p = argmax( P(数据|p) * P(p) )
-
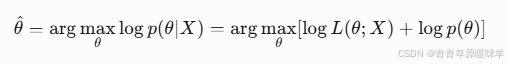
五、贝叶斯统计与朴素贝叶斯分类器
1. 贝叶斯统计
-
通俗解释:
用数据更新信念。比如先相信硬币是公平的(先验),根据抛硬币结果更新认知(后验)。-
公式:
后验概率 ∝ 似然 * 先验概率
-
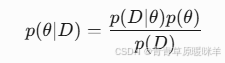
2. 朴素贝叶斯分类器
-
通俗解释:
基于特征独立的假设快速分类。比如根据词语判断邮件是否是垃圾。-
例子:
-
如果邮件包含“免费”和“赢大奖”,假设这两个词独立出现,计算联合概率判断是否为垃圾邮件。
-
-
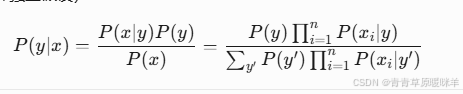
六、马尔可夫链与蒙特卡洛方法(MCMC)
1. 马尔可夫链
-
通俗解释:
下一个状态只依赖当前状态。比如天气预测:今天晴→明天雨的概率20%,晴→晴的概率80%。
![]()
2. 蒙特卡洛方法(MCMC)
-
通俗解释:
通过随机采样估算复杂概率。比如用撒豆子估算圆的面积。-
例子:MCMC从复杂分布中采样,用于贝叶斯后验估计。
-
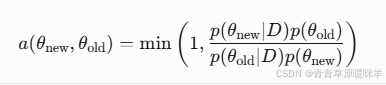























 888
888

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








