每日进步一点之灵魂拷问19之并查集数据结构

解释

#1
帮派问题如何解决？
例如：
给定一群人，和人之间的关系，如何确定每个人属于哪个关系圈？

#2
设定如下：
i 表示 某个人
s[i] 表示 the set of i person, i 这个人属于哪个集合（帮派）—-动态概念。

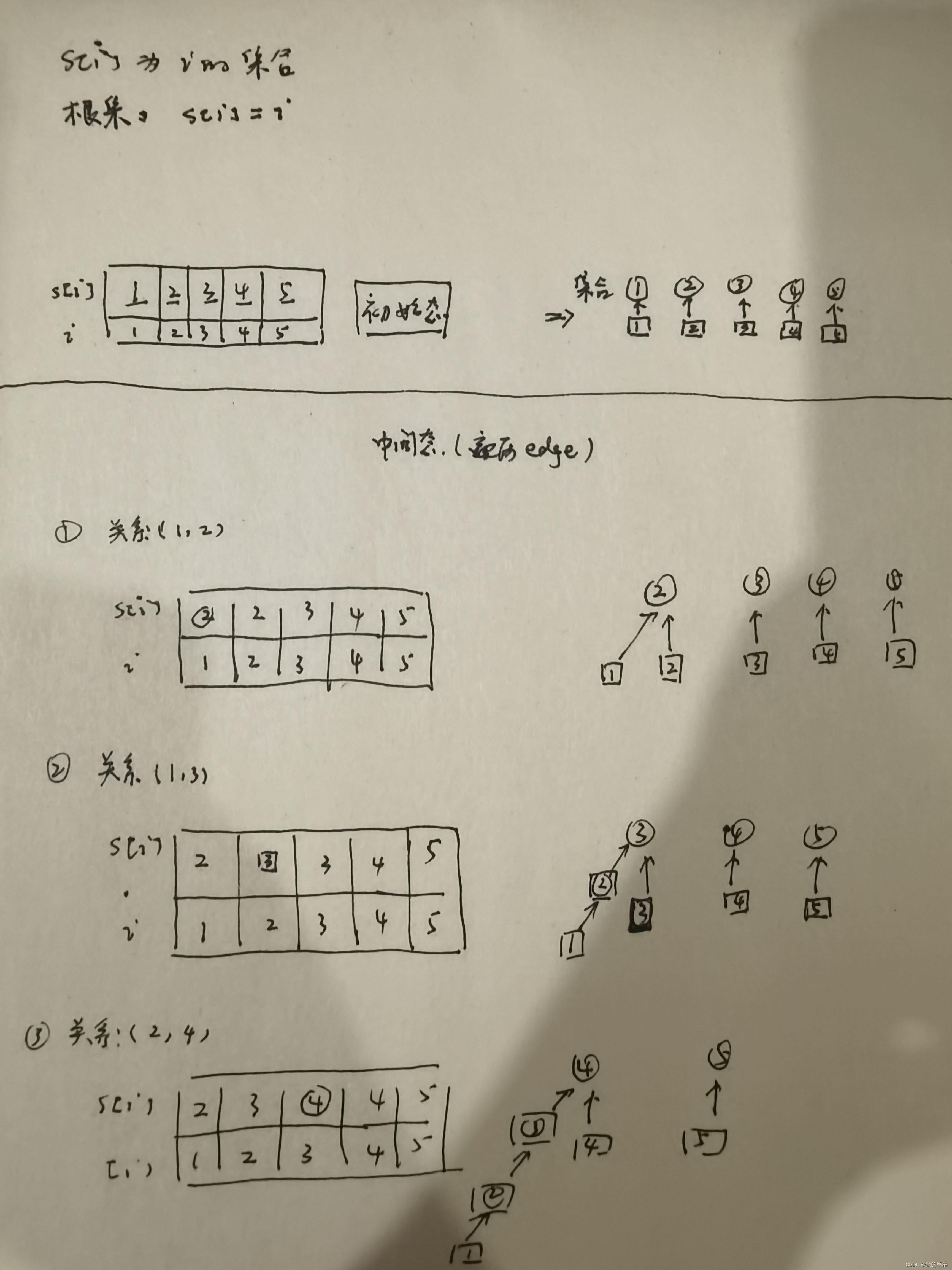
根据 对 动态事物关系的描述，向来都是动态的，因此具备基本三态模型：
1. 初始态
2. 中间态
3. 终态
那么，对于s[i] 它的演化三态，分别是什么？
简单来说，就是s[i]这个值会不会变？会的话，初始是什么样？最终你想变成什么样？

#3
s[x] = x 表示什么意思？

#4
并查集核心函数union_set和find_set？

def find_set(x):
	if s[x]!=x:
		# not the root set
		return find_set(s[x])
	else:
		return x

def union_set(x, y):
	x = find_set(x)
	y = find_set(y)
	if x!=y: #if the root of x != the root of y
		s[x] = s[y]

#5
上述函数方法复杂度为？可以优化么？优化后的复杂度？

# 路径压缩
def find_set(x):
	if x!=s[x]:
		s[x] = find_set(x)
	return s[x]



#基于高度合并
height = [0 for i in range(n)]
def union_set(x,y):
	x = find_set(x)
	y = find_set(y)
	if height[x] == height[y]:
		height[x] = height[x] + 1		#合并，树的高度+1
		s[y] = x
	else:						#矮树并到高树上，高树的高度保持不变
		if height[x] < height[y]:
			s[x] = y
		else:
			s[y] = x
	

#6
上述的find_set(x)是递归版本，那么如果数据规模大，可能会爆栈；怎么办？

def find_set(x):
	r = x
	while s[r]!=r:
		r = s[r]
	# so we find the root set of x
	
	# now let us update all the imediate elemetnts’ root set
	i = x
	while i!=r:
		tmp = s[i]
		s[i] = r #update 
		i = tmp
	return r

#7
路径压缩

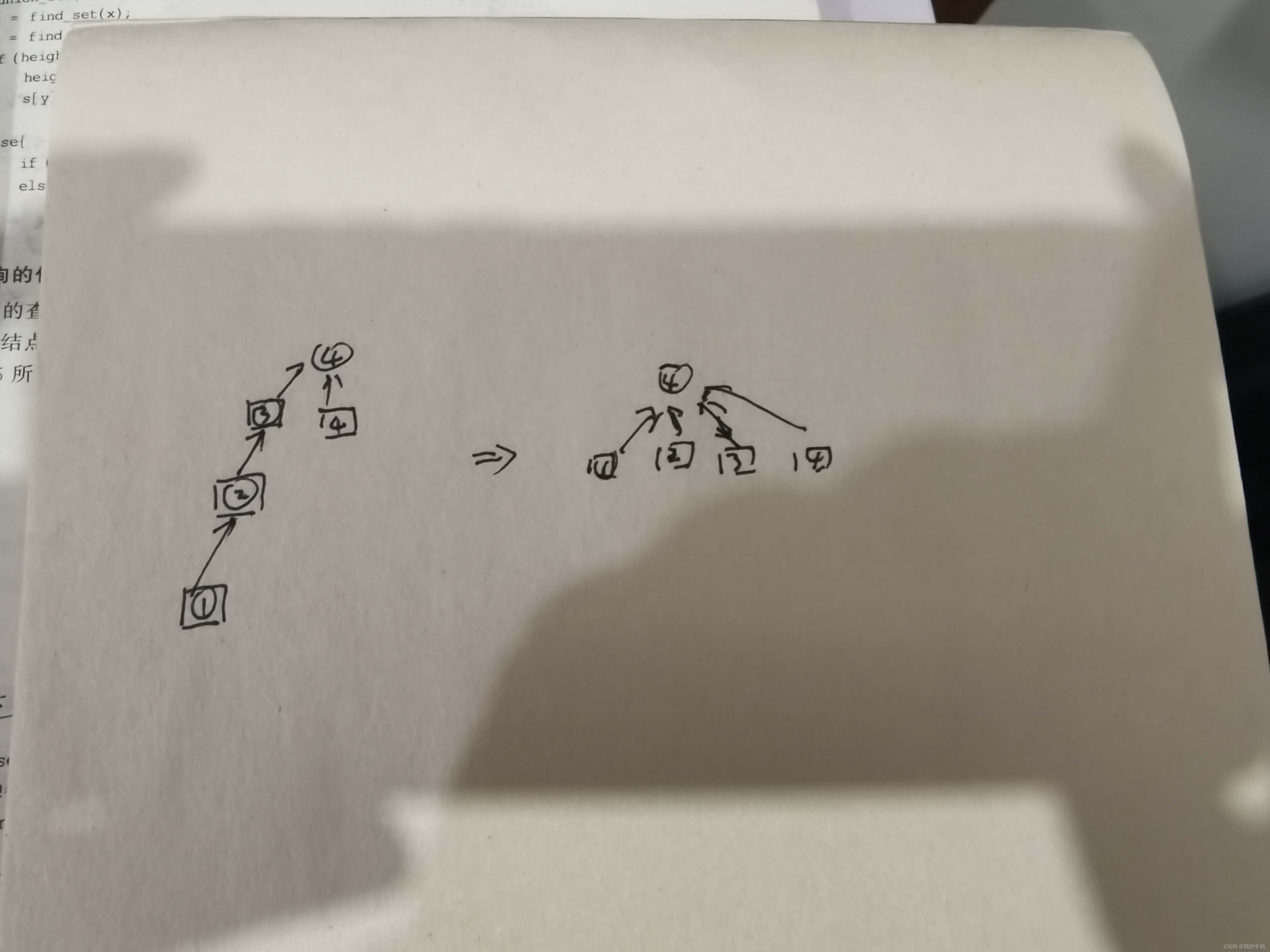
并查集模板

class UF:
    # 连通分量个数
    _count: int
    # 存储每个节点的父节点
    parent: List[int]

    # n 为图中节点的个数
    def __init__(self, n: int):
        self._count = n
        self.parent = [i for i in range(n)]

    # 将节点 p 和节点 q 连通
    def union(self, p: int, q: int):
        rootP = self.find(p)
        rootQ = self.find(q)

        if rootP == rootQ:
            return

        self.parent[rootQ] = rootP
        # 两个连通分量合并成一个连通分量
        self._count -= 1

    # 判断节点 p 和节点 q 是否连通
    def connected(self, p: int, q: int) -> bool:
        rootP = self.find(p)
        rootQ = self.find(q)
        return rootP == rootQ

    def find(self, x: int) -> int:
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    # 返回图中的连通分量个数
    def count(self) -> int:
        return self._count

应用举例

无向图中的连通量个数

创建并查集
union有关系的节点p和q
统计最后的count

class Solution:
    def countComponents(self, n: int, edges: list[list[int]]) -> int:
        uf = UF(n)
        for e in edges:
            uf.union(e[0], e[1])
        return uf.count()

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        n = len(isConnected)
        uf = UF(n)
        for i in range(n):
            for j in range(i + 1, n):
                # 如果两个城市是相连的，那么它们属于同一个连通分量
                if isConnected[i][j] == 1:
                    uf.union(i, j)
        return uf.count()