卷积和转置卷积
基础图像变换操作
1 空间域
-
Gamma Correction 伽马校正
v ′ = α v γ v' = \alpha v^{\gamma} v′=αvγ第一:图像像素值(v)代表着亮度(Brightness)
第二: γ > 1 \gamma>1 γ>1的时候,高亮度区域的变化大即细节增加,低亮度细节减少。 -
sober算子
边缘检测
具体可以搜索百度百科
2 频域
傅里叶变化
高频为细节,为轮廓。
低通滤波可以过滤细节。
图像特征提取
- SIFT:scale-invariant feature Transform
- 首先计算 金字塔表示(Pyramid Representation)
高斯滤波 + 下采样 - 找到图像金字塔中的特征点:
拉普拉斯滤波器
通过之前的高斯滤波和拉普拉斯整合可以成为, LoG高斯拉普拉斯滤波器。
LoG 计算代价高,用DoG近似。
- 首先计算 金字塔表示(Pyramid Representation)
卷积层
- 卷积
- 转置卷积,反卷积
【如果想了解怎么卷积?怎么反卷积?如何形成卷积矩阵和数据列向量的乘积???请看Im2Col GEMM】
我就搬运图,过程如下:
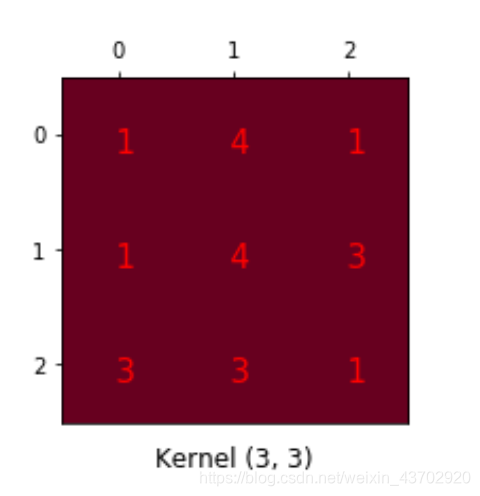
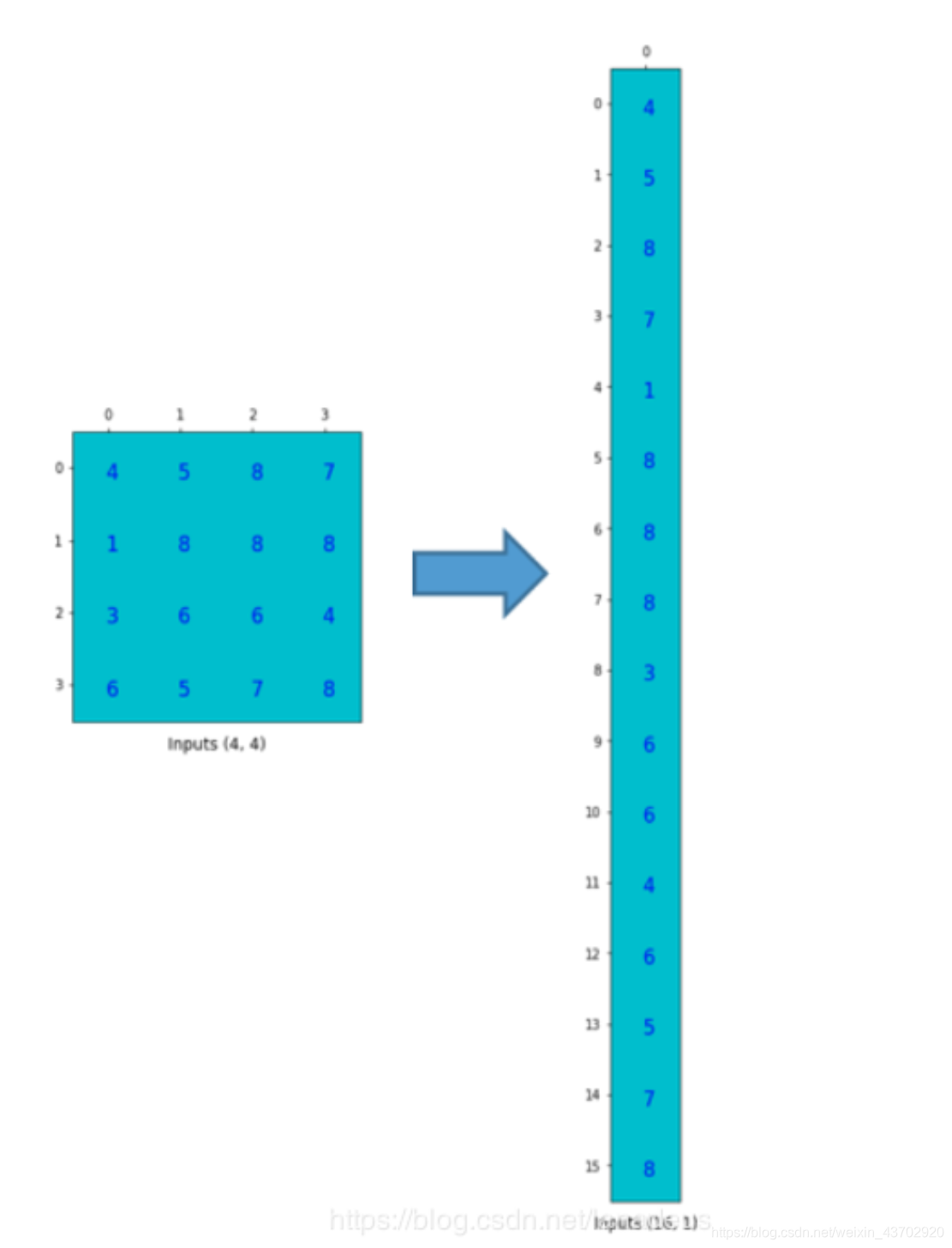
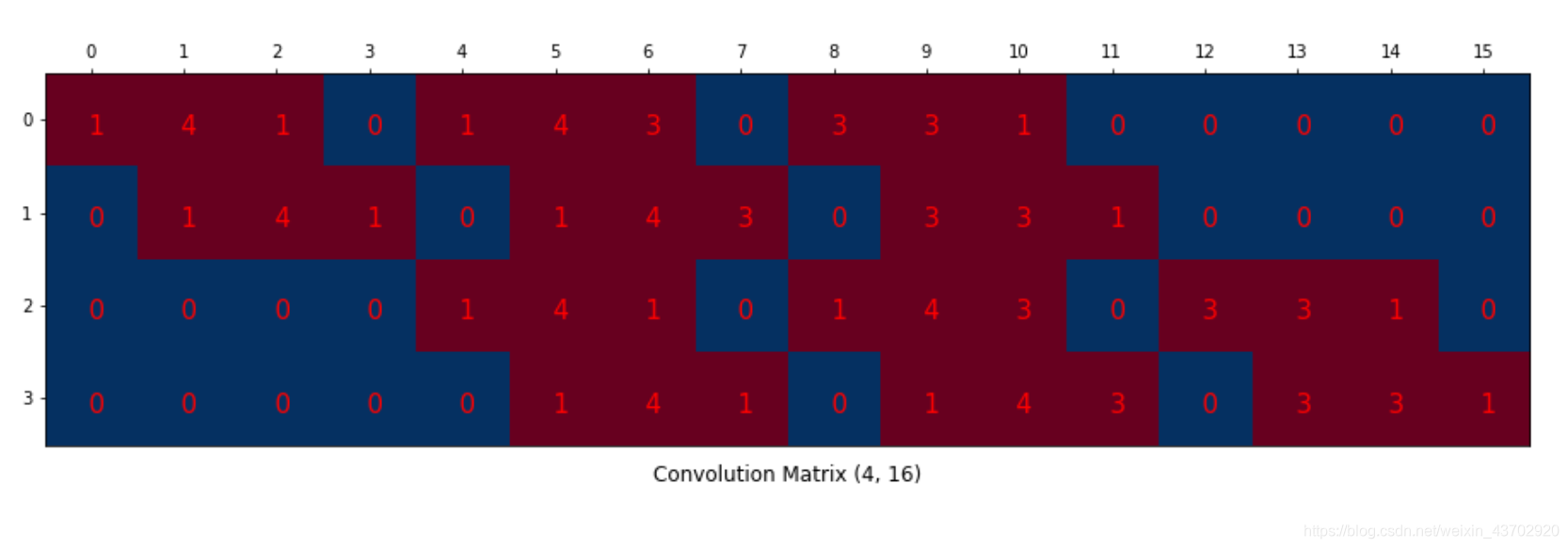
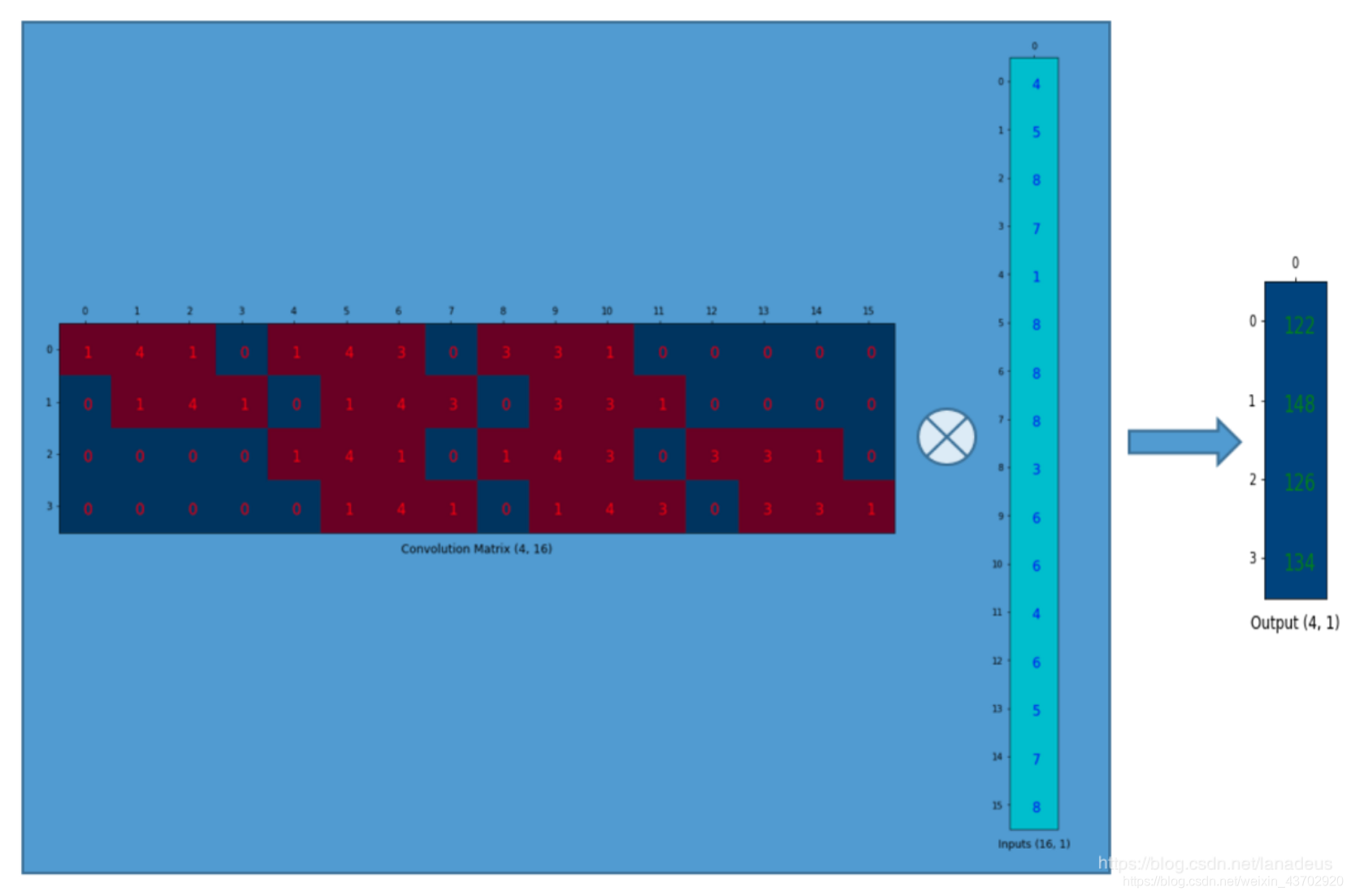
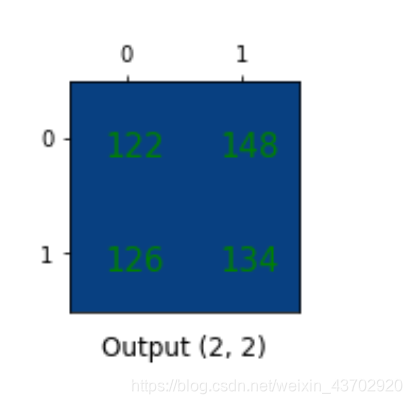
转置卷积
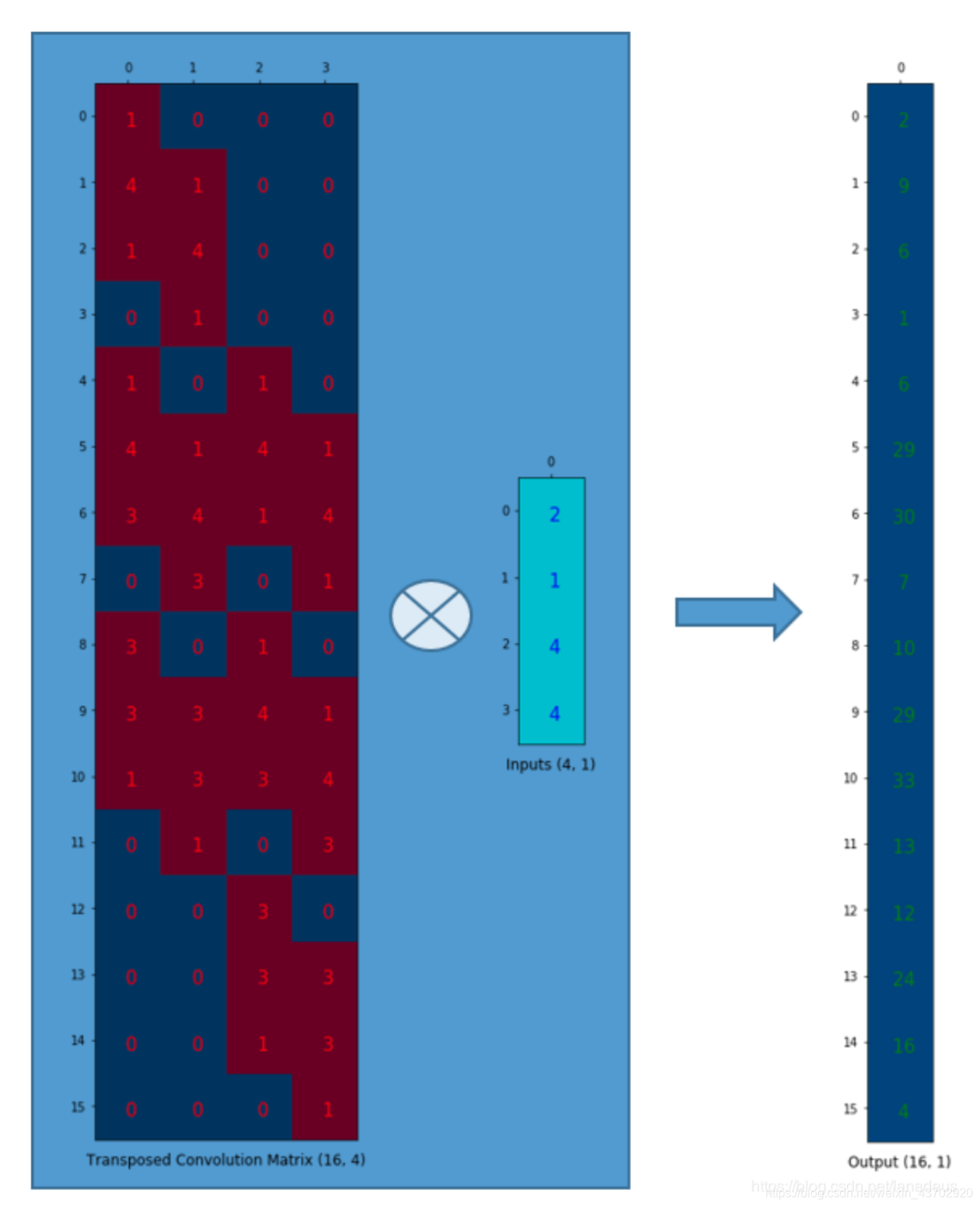
二维卷积下,默认的pytorch输入张量为 N,C,H,W
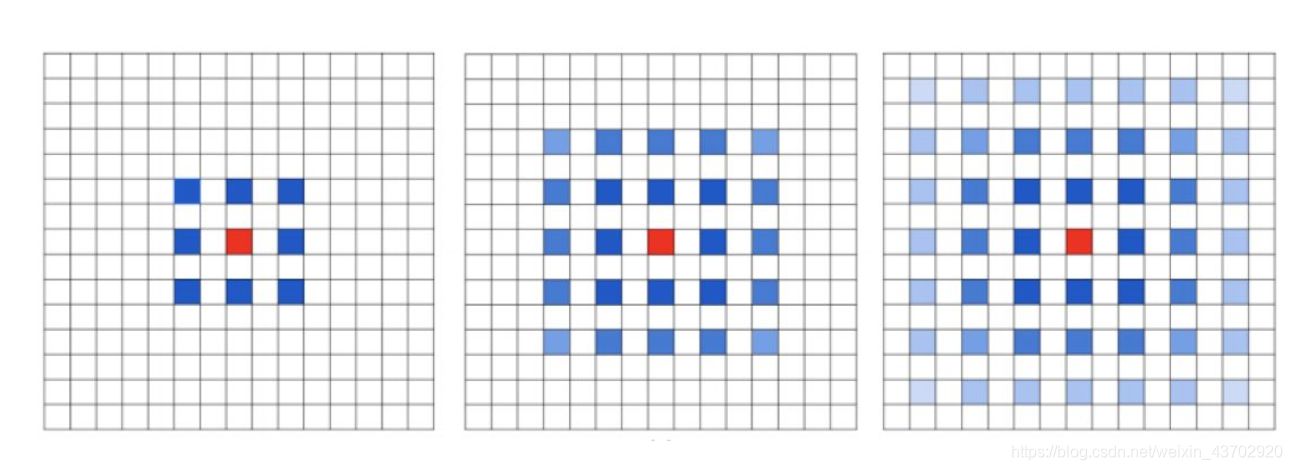
dilation 扩张卷积,增加感受野
transposed 控制是否进行转置卷积,也就是反卷积
归一化层(Normalization Layer)
归一化都采取以下公式:
y = γ x − E ( x ) V a r ( x ) + ϵ + β \bold y = \gamma \frac{\bold x - E(\bold x)}{\sqrt{\bold{Var(x)+\epsilon}}} + \beta y=γVar(x)+ϵx−E(x)+β
批次归一化:Batch Normalization Layer
对于全连接层:
进入神经元前的输入,进行批归一化。
因此你针对的是每个神经元!,每个神经元的输入进行多数据平均。
图中 Z Z Z表示的就是输入到第一个神经元的输出, x 1 x^1 x1就是批次里第一个数据。
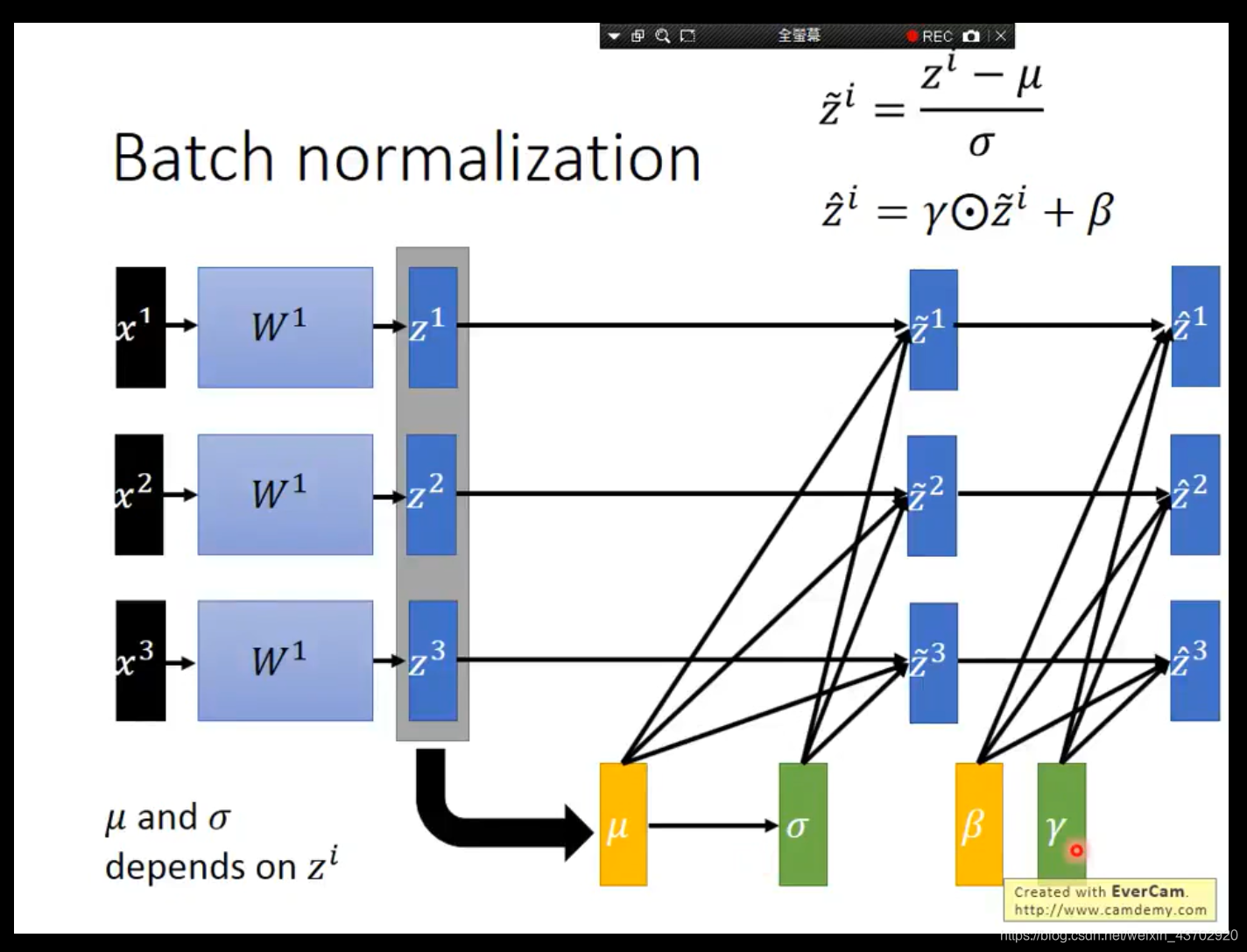
N , C , H , W = = > C × 1 N,C,H,W==>C \times 1 N,C,H,W==>C×1

- BatchNorm1d | BatchNorm2d | BatchNorm3d |
class troch.nn.BactchNorm2d(num_features, eps=1e-5, momentum=0.1, affine =True, track_running_states = True)
-
nums_features: 输入通道数目C
-
eps: 防止分母为0
-
momentum 控制指数移动平均计算 E ( x ) 和 V a r ( x ) E(\bold x) 和 Var(\bold x) E(x)和Var(x), 如果不用,则
track_running_stats=False,就用如下更新:
x ^ n e w = ( 1 − α ) x t − 1 + α x t ^ \hat x_{new} = (1-\alpha)x_{t-1} + \alpha \hat{x_t} x^new=(1−α)x





 本文深入探讨了卷积神经网络中的关键概念,包括卷积、转置卷积和各种归一化技术,如批次归一化、组归一化、实例归一化、层归一化和局部响应归一化。详细解析了每种技术的工作原理及在不同场景下的应用。
本文深入探讨了卷积神经网络中的关键概念,包括卷积、转置卷积和各种归一化技术,如批次归一化、组归一化、实例归一化、层归一化和局部响应归一化。详细解析了每种技术的工作原理及在不同场景下的应用。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 8586
8586

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










